Coordinate Geometry Exercise 14.1 (Part-13) | Extra Documents, Videos & Tests for Class 10 PDF Download
Question 8: Find the area of the triangle PQR with Q(3, 2) and the mid-points of the sides through Q being (2, −1) and (1, 2).
Answer : Let P(x1, y1), Q(3, 2) and R(x2, y2) be the vertices of the ∆PQR.
Suppose S(2, −1) and T(1, 2) be the mid-points of sides QR and PQ, respectively.

Using mid-point formula, we have
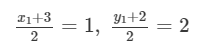
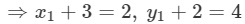
⇒x1=−1, y1=2
Coordinates of P = (−1, 2)
Also,

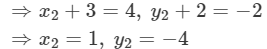
Coordinates of R = (1, −4)
So, P(−1, 2), Q(3, 2) and R(1, −4) are the vertices of ∆PQR.
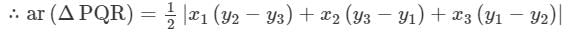

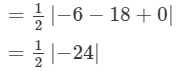
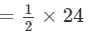
=12 square units
Hence, the area of the triangle is 12 square units.
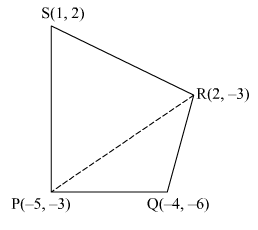
Question 9: If P(−5, −3), Q(−4, −6), R(2, −3) and S(1, 2) are the vertices of a quadrilateral PQRS, find its area.
Answer : It is given that P(−5, −3), Q(−4, −6), R(2, −3) and S(1, 2) are the vertices of a quadrilateral PQRS.
Area of the quadrilateral PQRS = Area of ∆PQR + Area of ∆PRS
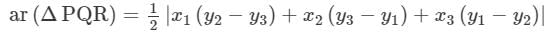
=1/2|−5[−6−(−3)]+(−4)[−3−(−3)]+2[−3−(−6)]|
=1/2|15+0+6|
= 21/2 square units
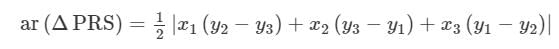
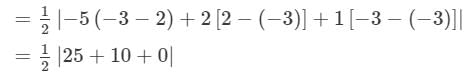
= 35/2 square units
∴ Area of the quadrilateral PQRS = 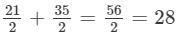 square units
square units
Hence, the area of the given quarilateral is 28 square units.
Question 10: If A(−3, 5), B(−2, −7), C(1, −8) and D(6, 3) are the vertices of a quadrilateral ABCD, find its area.
Answer : It is given that A(−3, 5), B(−2, −7), C(1, −8) and D(6, 3) are the vertices of a quadrilateral ABCD.

Area of the quadrilateral ABCD = Area of ∆ABC + Area of ∆ACD
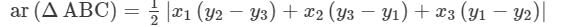
=1/2
|−3[−7−(−8)]+(−2)(−8−5)+1[5−(−7)]|
=1/2|−3+26+12|
=35/2 square units

=1/2|−3(−8−3)+1(3−5)+6[5−(−8)]|
=1/2|33−2+78|
= 109/2 square units
∴ Area of the quadrilateral ABCD = 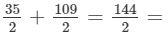 72 square units
72 square units
Hence, the area of the given quadrilateral is 72 square units.
Question 11: For what value of a the point (a, 1), (1, −1), and (11, 4) are collinear?
Answer : The formula for the area ‘A’ encompassed by three points ,
,  and
and  is given by the formula,
is given by the formula,
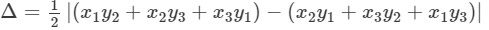
If three points are collinear the area encompassed by them is equal to 0.
The three given points are A(a, 1), B(1, −1) and C(11, 4). It is also said that they are collinear and hence the area enclosed by them should be 0.
Δ=1/2 |(x1y2+x2y3+x3y1)−(x2y1+x3y2+x1y3)|
0=1/2 |(a×−1+1×4+11×1)−(1×1+11×−1+a×4)|
0=1/2 | (−a+4+11)−(1−11+4a)|
0=1/2|(−a+15)−(−10+4a)|
0=1/2|−a+15+10−4a|
0=1/2|−5a+25|
0=−5a+25
5a=25
a=5
Hence the value of ‘a’ for which the given points are collinear is .
.
Question 12:Prove that the points (a, b), (a1, b1) and (a −a1, b −b1) are collinear if ab1 = a1b.
Answer : The formula for the area ‘A’ encompassed by three points ,
,  and
and  is given by the formula,
is given by the formula,
Δ=1/2|(x1y2+x2y3+x3y1)−(x2y1+x3y2+x1y3)|
If three points are collinear the area encompassed by them is equal to 0.
The three given points are ,
, and
and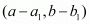 . If they are collinear then the area enclosed by them should be 0.
. If they are collinear then the area enclosed by them should be 0.
Δ=1/2|(ab1+a1(b−b1)+(a−a1)b)−(a1b+(a−a1)b1+a(b−b1))|
0=1/2|(ab1+a1b−a1b1+ab−a1b)−(a1b+ab1−a1b1+ab−ab1)|
0=1/2|ab1+a1b−a1b1+ab−a1b−a1b−ab1+a1b1−ab+ab1|
0=ab1−a1b
ab1=a1b
Hence we have proved that for the given conditions to be satisfied we need to have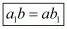 .
.
Question 13: If the vertices of a triangle are (1, −3), (4, p) and (−9, 7) and its area is 15 sq. units, find the value(s) of p.
Answer : Let A(1, −3), B(4, p) and C(−9, 7) be the vertices of the ∆ABC.
Here, x1 = 1, y1 = −3; x2 = 4, y2 = p and x3 = −9, y3 = 7
ar(∆ABC) = 15 square units
⇒1/2|x1(y2−y3)+x2(y3−y1)+x3(y1−y2)|=15⇒1/2|1(p−7)+4[7−(−3)]+(−9)(−3−p)|=15⇒1/2|p−7+40+27+9p|=15⇒|10p+60|=30
⇒10p+60=30 or 10p+60=−30
⇒10p=−30 or 10p=−90
⇒p=−3 or p=−9
Hence, the value of p is −3 or −9.
Question 14: If (x, y) be on the line joining the two points (1, −3) and (−4, 2) , prove that x + y + 2= 0.
Answer : Since the point (x, y) lie on the line joining the points (1, −3) and (−4, 2); the area of triangle formed by these points is 0.
That is,
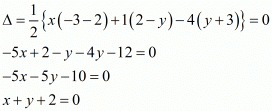
Thus, the result is proved.
Question 15: Find the value of k if points A(k, 3), B(6, −2) and C(−3, 4) are collinear.
Answer : The formula for the area ‘A’ encompassed by three points ,
,  and
and  is given by the formula,
is given by the formula,
Δ=1/2|(x1y2+x2y3+x3y1)−(x2y1+x3y2+x1y3)|
If three points are collinear the area encompassed by them is equal to 0.
The three given points are A(k, 3), B(6, −2) and C(−3, 4). It is also said that they are collinear and hence the area enclosed by them should be 0.
Δ=1/2|(k(−2)+6×4+(−3)×3)−(6×3+(−3)(−2)+k×4)| 0=1/2|(−2k+24−9)−(18+6+4k)| 0=1/2|−2k+15−24−4k| 0=1/2|−6k−9| 0=−6k−9 k=−9/6 =−3/2
Hence the value of ‘k’ for which the given points are collinear is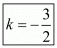 .
.
Question 16: Find the value of k, if the points A(7, −2), B (5, 1) and C (3, 2k) are collinear.
Answer : The formula for the area ‘A’ encompassed by three points ,
,  and
and  is given by the formula,
is given by the formula,
Δ=1/2|(x1y2+x2y3+x3y1)−(x2y1+x3y2+x1y3)|
If three points are collinear the area encompassed by them is equal to 0.
The three given points are A(7, −2), B(5, 1) and C(3, 2k). It is also said that they are collinear and hence the area enclosed by them should be 0.
Δ=1/2|(7×1+5×2k+3×−2)−(5×−2+3×1+7×2k)| 0=1/2|(7+10k−6)−(−10+3+14k)| 0=1/2|−4k+8| 0=−4k+8 k=2
Hence the value of ‘k’ for which the given points are collinear is .
.
Question 17: If the point P (m, 3) lies on the line segment joining the points A(−2/5,6) and B (2, 8), find the value of m.
Answer : The formula for the area ‘A’ encompassed by three points ,
,  and
and  is given by the formula,
is given by the formula,
Δ=1/2|(x1y2+x2y3+x3y1)−(x2y1+x3y2+x1y3)|
If three points are collinear the area encompassed by them is equal to 0.
It is said that the point P(m,3) lies on the line segment joining the points 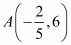 and B(2,8). Hence we understand that these three points are collinear. So the area enclosed by them should be 0.
and B(2,8). Hence we understand that these three points are collinear. So the area enclosed by them should be 0.
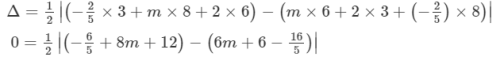
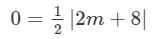
0=2m+8 m=−4
Hence the value of ‘m’ for which the given condition is satisfied is .
.
Question 18: If R (x, y) is a point on the line segment joining the points P (a, b) and Q (b, a), then prove that x + y = a + b.
Answer : The formula for the area ‘A’ encompassed by three points ,
,  and
and  is given by the formula,
is given by the formula,
Δ=1/2|(x1y2+x2y3+x3y1)−(x2y1+x3y2+x1y3)|
If three points are collinear the area encompassed by them is equal to 0.
It is said that the point R(x, y) lies on the line segment joining the points P(a, b) and Q(b, a). Hence we understand that these three points are collinear. So the area enclosed by them should be 0.

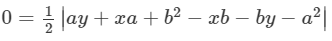
0=ay+xa+b2−xb−by−a2 a2−b2=ax+ay−bx−by (a+b)(a−b)=(a−b)(x+y) (a+b)=(x+y)
Hence under the given conditions we have proved that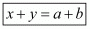 .
.
Question 19: Find the value of k, if the points A (8, 1) B(3, −4) and C(2, k) are collinear.
Answer : The formula for the area ‘A’ encompassed by three points ,
,  and
and  is given by the formula,
is given by the formula,
Δ=1/2|(x1y2+x2y3+x3y1)−(x2y1+x3y2+x1y3)|
If three points are collinear the area encompassed by them is equal to 0.
The three given points are A(8,1), B(3,−4) and C(2,k). It is also said that they are collinear and hence the area enclosed by them should be 0.
Δ=1/2|(8×−4+3×k+2×1)−(3×1+2×−4+8×k)| 0=1/2|(−32+3k+2)−(3−8+8k)| 0=1/2|−25−5k|k=−5
Hence the value of ‘k’ for which the given points are collinear is .
.
Question 20:Find the value of a for which the area of the triangle formed by the points A(a, 2a), B(−2, 6) and C(3, 1) is 10 square units.
Answer : The formula for the area ‘A’ encompassed by three points ,
,  and
and  is given by the formula,
is given by the formula,
Δ=1/2|(x1y2+x2y3+x3y1)−(x2y1+x3y2+x1y3)|
The three given points are A(a,2a), B(−2,6) and C(3,1). It is also said that the area enclosed by them is 10 square units. Substituting these values in the above mentioned formula we have,
Δ=1/2|(a×6+(−2)×1+3×2a)−((−2)×2a+3×6+a×1)|10=1/2|(6a−2+6a)−(−4a+18+a)|10=1/2|15a−20|20=|15a−20|4=|3a−4|
We have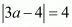 . Hence either
. Hence either
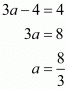
Or
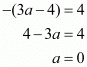
Hence the values of ‘a’ which satisfies the given conditions are .
.
Question 21: Prove that the points (a, 0), (0, b) and (1, 1) are collinear if  =1.
=1.
Answer : The formula for the area ‘A’ encompassed by three points ,
,  and
and  is given by the formula,
is given by the formula,
We know area of triangle formed by three points 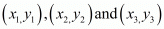 is given by
is given by
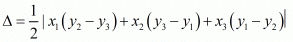
If three points are collinear the area encompassed by them is equal to 0.
The three given points are A(a,0), B(0,b) and C(1,1).
A =1/2|a(b−1)+1(0−b)|=1/2|ab−a−b|
It is given that 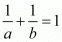
So we have,
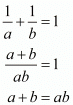
Using this in the previously arrived equation for area we have,

Since the area enclosed by the three points is equal to 0, the three points need to be .
.
Question 22: The point A divides the join of P (−5, 1) and Q(3, 5) in the ratio k:1. Find the two values of k for which the area of ΔABC where B is (1, 5) and C(7, −2) is equal to 2 units.
Answer : GIVEN: point A divides the line segment joining P (−5, 1) and Q (3, −5) in the ratio k: 1
Coordinates of point B (1, 5) and C (7, −2)
TO FIND: The value of k
PROOF: point A divides the line segment joining P (−5, 1) and Q (3, −5) in the ratio k: 1
So the coordinates of A are 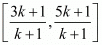
We know area of triangle formed by three points 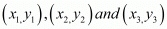 is given by Δ=12|(x1y2+x2y3+x3y1)−(x2y1+x3y2+x1y3)|
is given by Δ=12|(x1y2+x2y3+x3y1)−(x2y1+x3y2+x1y3)|
Now Area of ΔABC= 2 sq units.
Taking three points A  , B (1, 5) and C (7, −2)
, B (1, 5) and C (7, −2)
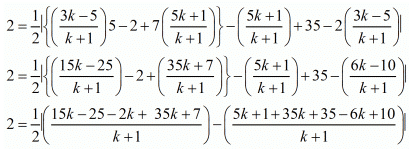
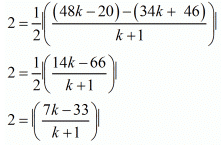
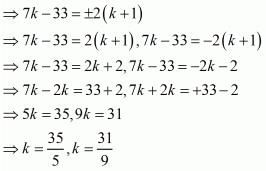
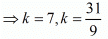
Hence 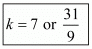
Question 23: The area of a triangle is 5. Two of its vertices are (2, 1) and (3, −2). The third vertex lies on y = x + 3. Find the third vertex.
Answer : GIVEN: The area of triangle is 5.Two of its vertices are (2, 1) and (3, −2). The third vertex lies on y= x+3
TO FIND: The third vertex.
PROOF: Let the third vertex be (x, y)
We know area of triangle formed by three points 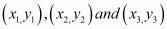 is given by Δ=12|(x1y2+x2y3+x3y1)−(x2y1+x3y2+x1y3)|
is given by Δ=12|(x1y2+x2y3+x3y1)−(x2y1+x3y2+x1y3)|
Now
Taking three points(x, y), (2, 1) and (3, −2)
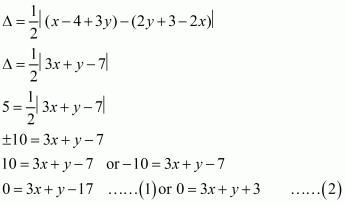
Also it is given the third vertex lies on y = x+3
Substituting the value in equation (1) and (2) we get

Hence the coordinates of 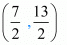 and
and 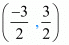
Question 24: If  , prove that the points (a, a2), (b, b2), (c, c2) can never be collinear.
, prove that the points (a, a2), (b, b2), (c, c2) can never be collinear.
Answer : GIVEN: If 
TO PROVE: that the points 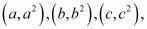 can never be collinear.
can never be collinear.
PROOF:
We know three points 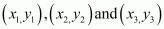 are collinear when
are collinear when 
Now taking three points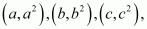

Also it is given that
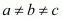
Hence area of triangle made by these points is never zero. Hence given points are never collinear.
Question 25: Four points A (6, 3), B (−3, 5), C(4, −2) and D (x, 3x) are given in such a way that  find x.
find x.
Answer : GIVEN: four points A (6, 3), B (−3, 5) C (4, −2) and D(x, 3x) such that 
TO FIND: the value of x
PROOF:
We know area of the triangles formed by three points 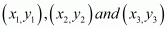 is given by
is given by 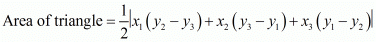
Now
Area of triangle DBC taking D(x, 3x), B (−3, 5), C (4, −2)
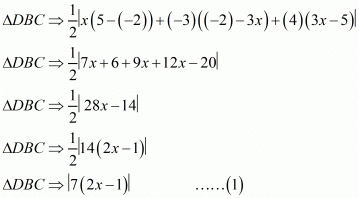
Area of triangle ABC taking, A (6, 3), B (−3, 5), C (4, −2)

Also it is given that

Substituting the values from (1) and (2) we get

Question 26: If three points (x1, y1) (x2, y2), (x3, y3) lie on the same line, prove that 
Answer : GIVEN: If three points  lie on the same line
lie on the same line
TO PROVE: 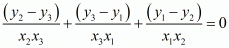
PROOF:
We know that three points 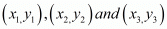 are collinear if
are collinear if
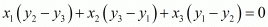

Hence proved.
|
5 videos|292 docs|59 tests
|
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|
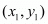
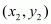
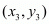
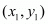
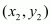
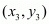
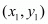
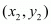
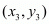
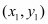 ,
, 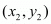 and
and 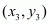 is given by the formula,
is given by the formula,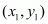
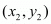
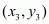
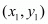 ,
, 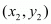 and
and  is given by the formula,
is given by the formula, ,
,  and
and  is given by the formula,
is given by the formula,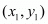
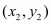
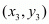

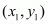 ,
, 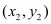 and
and 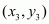 is given by the formula,
is given by the formula,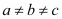 , prove that the points (a, a2), (b, b2), (c, c2) can never be collinear.
, prove that the points (a, a2), (b, b2), (c, c2) can never be collinear.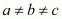
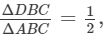
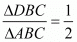
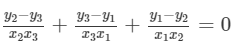
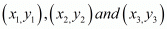 lie on the same line
lie on the same line















