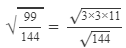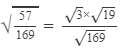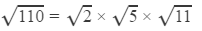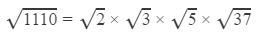Class 8 Exam > Class 8 Notes > RD Sharma Solutions for Class 8 Mathematics > RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7)
RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7) | RD Sharma Solutions for Class 8 Mathematics PDF Download
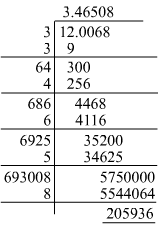
Question 2: Find the square root of 12.0068 correct to four decimal places.
Answer 2:
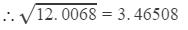
We can round it off to four decimal places, i.e. 3.4651.
Question 3: Find the square root of 11 correct to five decimal places.
Answer 3: Using the long division method:
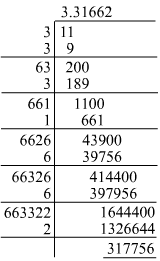
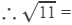3.31662
Question 4: Given that: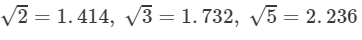
and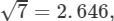 
evaluate each of the following:
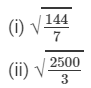
Answer 4: Given: √7 = 2.646
(i)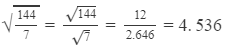 
Given: √3 = 1.732
(ii)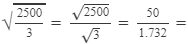 
28.867
Question 5: Given that: 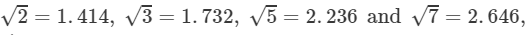find the square roots of the following:
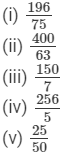
Answer 5: From the given values, we can simplify the expressions in the following manner:
(i)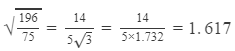 
(ii)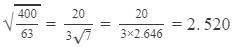 
(iii)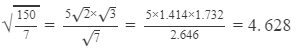 
(iv)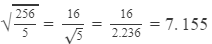 
(v)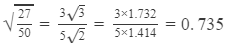 
Question 6: Using square root table, find the square root
7
Answer 6: From the table, we directly find that the square root of 7 is 2.646.
Question 7: Using square root table, find the square root
15
Answer 7: Using the table to find √3 and √5
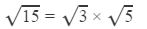
=1.732×2.236=3.873
Question 8:Using square root table, find the square root 74
Answer 8: Using the table to find
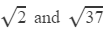
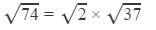
=1.414×6.083
=8.602
Question 9: Using square root table, find the square root 82
Answer 9: Using the table to find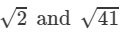
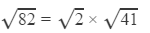
=1.414×6.403
=9.055
Question 10: Using square root table, find the square root 198
Answer 10: Using the table to find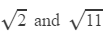
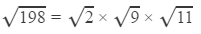
=1.414×3×3.317
= 14.070
Question 11: Using square root table, find the square root
540
Answer 11: Using the table to find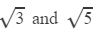
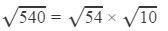
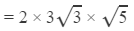
=2×3×1.732×2.2361
=23.24
Question 12: Using square root table, find the square root 8700
Answer 12: Using the table to find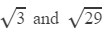
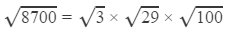
=1.7321×5.385×10
=93.27
Question 13: Using square root table, find the square root 3509
Answer 13: Using the table to find √29
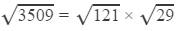
=11×5.3851
=59.235
Question 14: Using square root table, find the square root 6929
Answer 14: Using the table to find √14
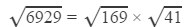
=13 ×6.4031
=83.239
Question 15: Using square root table, find the square root 25725
Answer 15: Using the table to find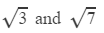
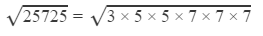
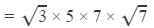
=1.732 ×5×7×2.646
=160.41
Question 16: Using square root table, find the square root 1312
Answer 16: Using the table to find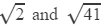
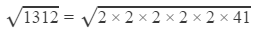
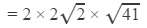
=2×2×1.414×6.4031
=36.222
Question 17: Using square root table, find the square root 4192
Answer 17: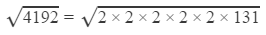
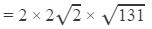
The square root of 131 is not listed in the table. Hence, we have to apply long division to find it.
Substituting the values:
= 2×2×11.4455 (using the table to find √2)
= 64.75
Question 18: Using square root table, find the square root 4955
Answer 18: On prime factorisation:
4955 is equal to 5 × 991, which means that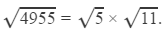
The square root of 991 is not listed in the table; it lists the square roots of all the numbers below 100.
Hence, we have to manipulate the number such that we get the square root of a number less than 100. This can be done in the following manner:
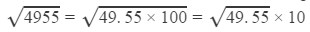
Now, we have to find the square root of 49.55.
We have: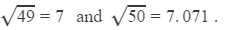 
Their difference is 0.071.
Thus, for the difference of 1 (50 − 49), the difference in the values of the square roots is 0.071.
For the difference of 0.55, the difference in the values of the square roots is:
0.55 × 0.0701 = 0.03905
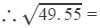7+0.03905=7.03905
Finally, we have:
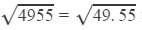×10=7.03905×10=70.3905
Question 19: Using square root table, find the square root 99/144
Answer 19:
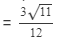
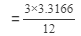(using the square root table to find √11)
=0.829
Question 20: Using square root table, find the square root 57/169
Answer 20:
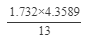(using the square root table to find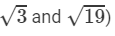 
0.581
Question 21: Using square root table, find the square root 101/169
Answer 21:
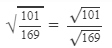
The square root of 101 is not listed in the table. This is because the table lists the square roots of all the numbers below 100.
Hence, we have to manipulate the number such that we get the square root of a number less than 100. This can be done in the following manner:
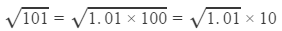
Now, we have to find the square root of 1.01.
We have:
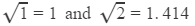
Their difference is 0.414.
Thus, for the difference of 1 (2 − 1), the difference in the values of the square roots is 0.414.
For the difference of 0.01, the difference in the values of the square roots is:
0.01 × 0.414 = 0.00414
∴ 
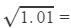1+0.00414=1.00414
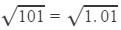×10=1.00414×10=10.0414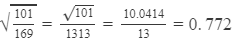 
This value is really close to the one from the key answer.
Question 22: Using square root table, find the square root
13.21
Answer 22: From the square root table, we have:
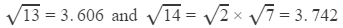
Their difference is 0.136.
Thus, for the difference of 1 (14 − 13), the difference in the values of the square roots is 0.136.
For the difference of 0.21, the difference in the values of their square roots is:
0.136×0.21=0.02856
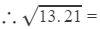3.606+0.02856≈3.635Question 23: Using square root table, find the square root
Answer 23: We have to find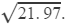
From the square root table, we have:
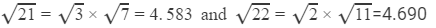
Their difference is 0.107.
Thus, for the difference of 1 (22 − 21), the difference in the values of the square roots is 0.107.
For the difference of 0.97, the difference in the values of their square roots is:
0.107×0.97=0.104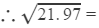
4.583+0.104≈4.687
Question 24: Using square root table, find the square root 110
Answer 24:
=1.414×2.236×3.317 (Using the square root table to find all the square roots)
=10.488
Question 25: Using square root table, find the square root
1110
Answer 25:
=1.414×1.732×2.236×6.083 (Using the table to find all the square roots )=33.312
Question 26: Using square root table, find the square root
11.11
Answer 26: We have:
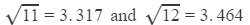
Their difference is 0.1474.
Thus, for the difference of 1 (12 − 11), the difference in the values of the square roots is 0.1474.
For the difference of 0.11, the difference in the values of the square roots is:
0.11 × 0.1474 = 0.0162
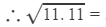3.3166+0.0162=3.328≈3.333
Question 27: The area of a square field is 325 m2. Find the approximate length of one side of the field.
Answer 27: The length of one side of the square field will be the square root of 325.
∴
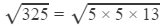
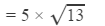
=5×3.605
=18.030
Hence, the length of one side of the field is 18.030 m.
Question 28: Find the length of a side of a sqiare, whose area is equal to the area of a rectangle with sides 240 m and 70 m.
Answer 28: The area of the rectangle = 240 m × 70 m = 16800 m2
Given that the area of the square is equal to the area of the rectangle.
Hence, the area of the square will also be 16800 m2.
The length of one side of a square is the square root of its area.
∴
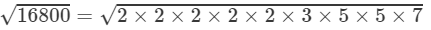
=2×2×5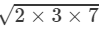 
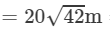=129.60 m
Hence, the length of one side of the square is 129.60 m
The document RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7) | RD Sharma Solutions for Class 8 Mathematics is a part of the Class 8 Course RD Sharma Solutions for Class 8 Mathematics.
All you need of Class 8 at this link: Class 8
FAQs on RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7) - RD Sharma Solutions for Class 8 Mathematics
| 1. What is the method to find the square root of a perfect square number? |  |
Ans. To find the square root of a perfect square number, we need to prime factorize the number and take one factor from each pair. The product of these factors will give us the square root of the given number.
| 2. How can we determine if a number is a perfect square or not? | |
Ans. To determine if a number is a perfect square or not, we can find its square root. If the square root is an integer, then the number is a perfect square. If the square root is a decimal or a non-terminating number, then the number is not a perfect square.
| 3. Can we find the square root of a negative number? | |
Ans. No, we cannot find the square root of a negative number. The square root of a number is always a non-negative number. If we want to find the square root of a negative number, we need to use complex numbers.
| 4. What is the square root of 0? | |
Ans. The square root of 0 is 0. Since 0 multiplied by 0 gives 0, the square root of 0 is the number that, when multiplied by itself, gives 0.
| 5. Is the square root of a number always positive? | |
Ans. The square root of a positive number is always positive. However, the square root of 0 is 0, which is neither positive nor negative. The square root of a negative number is a complex number, which has both a real and an imaginary part.
Related Exams
About this Document
|
4.93/5 Rating |
|
Dec 22, 2024 Last updated |
Document Description: RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7) for Class 8 2024 is part of RD Sharma Solutions for Class 8 Mathematics preparation.
The notes and questions for RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7) have been prepared according to the Class 8 exam syllabus. Information about RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7) covers topics
like and RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7) Example, for Class 8 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7).
Introduction of RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7) in English is available as part of our RD Sharma Solutions for Class 8 Mathematics
for Class 8 & RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7) in Hindi for RD Sharma Solutions for Class 8 Mathematics course.
Download more important topics related with notes, lectures and mock test series for Class 8
Exam by signing up for free. Class 8: RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7) | RD Sharma Solutions for Class 8 Mathematics
Description
Full syllabus notes, lecture & questions for RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7) | RD Sharma Solutions for Class 8 Mathematics - Class 8 | Plus excerises question with solution to help you revise complete syllabus for RD Sharma Solutions for Class 8 Mathematics | Best notes, free PDF download
Information about RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7)
In this doc you can find the meaning of RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7) defined & explained in the simplest way possible. Besides explaining types of
RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7) theory, EduRev gives you an ample number of questions to practice RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7) tests, examples and also practice Class 8
tests
|
Explore Courses for Class 8 exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
study material
,Exam
,Important questions
,RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7) | RD Sharma Solutions for Class 8 Mathematics
,Previous Year Questions with Solutions
,Semester Notes
,Free
,past year papers
,RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7) | RD Sharma Solutions for Class 8 Mathematics
,mock tests for examination
,Viva Questions
,ppt
,MCQs
,Summary
,Objective type Questions
,RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7) | RD Sharma Solutions for Class 8 Mathematics
,practice quizzes
,Sample Paper
,shortcuts and tricks
,video lectures
,Extra Questions
;
Additional Information about RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7) for Class 8 Preparation
RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7) Free PDF Download
The RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7) is an invaluable resource that delves deep into the core of the Class 8 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7) now and kickstart your journey towards success in the Class 8 exam.
Importance of RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7)
The importance of RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7) cannot be overstated, especially for Class 8 aspirants.
This document holds the key to success in the Class 8 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7) Notes
RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7) Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7).
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7) Notes on EduRev are your ultimate resource for success.
RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7) Class 8 Questions
The "RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7) Class 8 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 8 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7) on the App
Students of Class 8 can study RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7) alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7),
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of RD Sharma Solutions for Class 8 Math Chapter 3 - Squares and Square Roots (Part-7) is prepared as per the latest Class 8 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup