Chapter 20 - Mensuration - I (Part - 2), Class 8, Maths RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics PDF Download
PAGE NO 20.22:
Question 1:
Find the area, in square metres, of the trapezium whose bases and altitudes are as under:
(i) bases = 12 dm and 20 dm, altitude = 10 dm
(ii) bases = 28 cm and 3 dm, altitude = 25 cm
(iii) bases = 8 m and 60 dm, altitude = 40 dm
(iv) bases = 150 cm and 30 dm, altitude = 9 dm.
ANSWER:
(i)Given: Bases:12 dm = 12/10m = 1.2 m
And, 20 dm = 20/10m = 2 m
Altitude = 10 dm = 10/10m = 1 m
Area of trapezium = 1/2 × (Sum of the bases) × (Altitude)
= 1/2 × (1.2 + 2) m × (1) m
= 1.6 × m × m = 1.6 m²
(ii)Given: Bases:28 cm = 28/100m
= 0.28 m
And, 3 dm
= 310m = 0.3 m
Altitude = 25 cm = 25/100m = 0.25 m
Area of trapezium = 1/2 × (Sum of the bases) × (Altitude)
= 1/2 × (0.28 + 0.3) m × (0.25) m
= 0.0725 m²
(iii)Given:Bases:8 mAnd, 60 dm = 60/10m = 6 m
Altitude = 40 dm = 40/10m = 4 m
Area of trapezium = 1/2 × (Sum of the bases) × (Altitude)
= 1/2 × (8 + 6) m × (4) m
= 28 × m × m
= 28 m²
(iv)Given:Bases:150 cm = 150/100m
= 1.5 m
And, 30 dm = 30/10m
= 3 m
Altitude = 9 dm
= 9/10m = 0.9 m
Area of trapezium = 1/2 × (Sum of the bases) × (Altitude)
= 1/2 × (1.5 + 3) m × (0.9) m
= 2.025 × m × m
= 2.025 m²
Question 2:
Find the area of trapezium with base 15 cm and height 8 cm, if the side parallel to the given base is 9 cm long.
ANSWER:
Given:Lengths of the parallel sides are 15 cm and 9 cm.
Height = 8 cm
Area of trapezium = 1/2 × (Sum of the opposite sides) × (Distance between the parallel sides)
= 1/2 × (15 + 9) × (8)
= 96 cm²
Question 3:
Find the area of a trapezium whose parallel sides are of length 16 dm and 22 dm and whose height is 12 dm.
ANSWER:
Given:Lengths of the parallel sides are 16 dm and 22 dm.
And, height between the parallel sides is 12 dm.
Area of trapezium = 1/2 × (Sum of the parallel sides) × (Height)
= 1/2 × (16 + 22) × (1/2)
= 228 dm²
= 228 × dm × dm
= 228 × 1/10m × 1/10m
= 2.28 m²
Question 4:
Find the height of a trapezium, the sum of the lengths of whose bases (parallel sides) is 60 cm and whose area is 600 cm².
ANSWER:
Given: Sum of the parallel sides of a trapezium = 60 cm
Area of the trapezium = 600 cm²
Area of trapezium = 1/2 × (Sum of the parallel sides) × (Height)
On putting the values:600 = 12 × 60 × (Height)
600 = 30 × (Height)
Height = 600/30 = 20 cm
Question 5:
Find the altitude of a trapezium whose area is 65 cm² and whose bases are 13 cm and 26 cm.
ANSWER:
Given:Area of the trapezium = 65 cm²
The lengths of the opposite parallel sides are 13 cm and 26 cm.
Area of trapezium
= 1/2 × (Sum of parallel bases) × (Altitude)
On putting the values: 65 = 1/2 × (13 + 26) × (Altitude)
65 × 2 = 39 × Altitude
Altitude = 130/39 = 10/3 cm
Question 6:
Find the sum of the lengths of the bases of a trapezium whose area is 4.2 m² and whose height is 280 cm.
ANSWER:
Given:Area of the trapezium = 4.2 m²
Height = 280 cm = 280/100m = 2.8 m
Area of trapezium = 1/2 × (Sum of the parallel bases) × (Height)
4.2 = 1/2 × (Sum of the parallel bases) × 2.8
4.2 × 2 = (Sum of the parallel bases) × 2.8
Sum of the parallel bases = 8.4/2.8 = 3 m
Question 7:
Find the area of a trapezium whose parallel sides of lengths 10 cm and 15 cm are at a distance of 6 cm from each other. Calculate this area as
(i) the sum of the areas of two triangles and one rectangle.
(ii) the difference of the area of a rectangle and the sum of the areas of two triangles.
ANSWER:
Given:Length of the parallel sides of a trapezium are 10 cm and 15 cm. The distance between them is 6 cm.Let us extend the smaller side and then draw perpendiculars from the ends of both sides.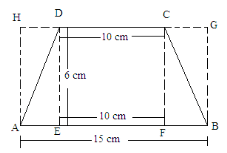
(i)Area of trapezium ABCD = (Area of rectangle EFCD) + (Area of triangle AED + Area of triangle BFC)
= (10 × 6) + [(1/2 × AE × ED) + (1/2 × BF × FC)]
= 60 + [(1/2 × AE × 6) + (1/2 × BF × 6)]
= 60 + [3AE + 3 BF]
= 60 + 3 × (AE + BF)
Here, AE + EF + FB = 15cm
And EF = 10 cm
∴ AE + 10 + BF = 15
Or, AE + BF = 15-10 = 5 cm
Putting this value in the above formula:
Area of the trapezium = 60 + 3 × (5) = 60 + 15 = 75 cm²
(ii) In this case, the figure will look as follows:
(ii) In this case, the figure will look as follows: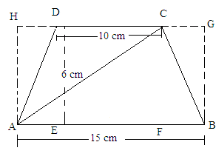
Area of trapezium ABCD = (Area of rectangle ABGH)-[(Area of triangle AHD) + (Area of triangle BGC)]
= (15 × 6)−[(1/2 × DH × 6) + (1/2 × GC × 6)]
= 90−[3 × DH + 3 × GC]
= 90−3[DH + GC]
Here, HD + DC + CG
= 15 cm
DC = 10 cm
HD + 10 + CG = 15
HD + GC = 15-10 = 5 cm
Putting this value in the above equation:
Area of the trapezium = 90-3(5) = 90-15 = 75 cm²
Question 8:
The area of a trapezium is 960 cm². If the parallel sides are 34 cm and 46 cm, find the distance between them.
ANSWER:
Given:Area of the trapezium = 960 cm²
And the length of the parallel sides are 34 cm and 46 cm.Area of trapezium
= 1/2 × (Sum of the parallel sides) × (Perpendicular distance between the parallel sides)
⇒ 960 = 1/2 × (34 + 46) × (Height)
⇒ 960 = 40 × (Height)
⇒ Height = 960/40 = 24 cm
PAGE NO 20.23:
Question 9:
Find the area of Fig. 20.35 as the sum of the areas of two trapezium and a rectangle.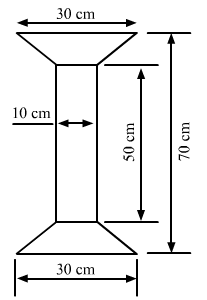
ANSWER:
The given figure is: 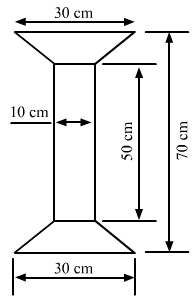
In the given figure, we have a rectangle of length 50 cm and width 10 cm, and two similar trapeziums with parallel sides as 30 cm and 10 cm at both ends.
Suppose x is the perpendicular distance between the parallel sides in both the trapeziums.
We have:
Total length of the given figure = Length of the rectangle + 2 × Perpendicular distance between the parallel sides in both the trapeziums
70 = 50 + 2 × x2 × x =
70-50 = 20x
= 202 = 10 cm
Now, area of the complete figure = (area of the rectangle with sides 50 cm and 10 cm) + 2 × (area of the trapezium with parallel sides 30 cm and 10 cm, and height 10 cm)
= (50 × 10) + 2 × [12 × (30 + 10) × (10)]
= 500 + 2 × [200]
= 900 cm²
PAGE NO 20.23:
Question 10:
Top surface of a table is trapezium in shape. Find its area if its parallel sides are 1 m and 1.2 m and perpendicular distance between them is 0.8 m.
ANSWER:
The given figure is: The given figure is: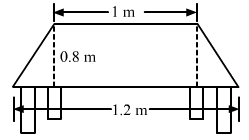
Lengths of the parallel sides are 1.2 m and 1 m and the perpendicular distance between them is 0.8 m.
∴ Area of the trapezium shaped surface = 12 × (Sum of the parallel sides) × (Perpendicular distance)
= 1/2 × (1.2 + 1) × (0.8)
= 1/2 × 2.2 × 0.8
= 0.88 m²
Question 11:
The cross-section of a canal is a trapezium in shape. If the canal is 10 m wide at the top 6 m wide at the bottom and the area of cross-section is 72 m² determine its depth.
ANSWER:
Let the depth of canal be d.Given:Lengths of the parallel sides of the trapezium shape canal are 10 m and 6 m.And, the area of the cross section of the canal is 72 m².
Area of trapezium = 1/2 × (Sum of the parallel sides) × (Perpendicular distance between the parallel sides)
72 = 1/2 × (10 + 6) × (d)
72 = 8 × dd = 72/8 = 9 m
:
Question 12:
The area of a trapezium is 91 cm² and its height is 7 cm. If one of the parallel sides is longer than the other by 8 cm, find the two parallel sides.
ANSWER:
Given: Area of the trapezium = 91 cm²
Height = 7 cm
Let the length of the smaller side be x.
Then, the length of longer side will be 8 more than smaller side, i.e. 8 + x.
Area of trapezium = 1/2 × (Sum of the parallel sides) × (Height)
⇒ 91 = 1/2 × [(8 + x) + x] × (7)
⇒ 91 = 7/2 × [8 + x + x]⇒ 91 × 2 = 7 × [8 + 2x]
We can rewrite it as follows:7 × [8 + 2x] = 182
⇒ [8 + 2x] = 182/7 = 26
⇒ 8 + 2x = 26
⇒ 2x = 26-8 = 18
⇒ x = 18/2 = 9 cm
∴ Length of the shorter side of the trapezium = 9 cm
And, length of the longer side = 8 + x = 8 + 9 = 17 cm
Question 13:
The area of a trapezium is 384 cm². Its parallel sides are in the ratio 3 : 5 and the perpendicular distance between them is 12 cm. Find the length of each one of the parallel sides.
ANSWER:
Given:Area of the trapezium = 384 cm²
The parallel sides are in the ratio 3:5 and the perpendicular height between them is 12 cm.
Suppose that the sides are in x multiples of each other.
Then, length of the shorter side = 3x
Length of the longer side = 5x
Area of a trapezium = 1/2 × (Sum of parallel sides) × (Height)
⇒ 384 = 1/2 × (3x + 5x) × (12)
⇒ 384 = 12/2 × (8x)
⇒ 384 = 6 × (8x)
⇒ 8x = 384/6 = 64
⇒ x = 64/8 = 8 cm
∴ Length of the shorter side = 3 × x = 3 × 8 = 24 cm
And, length of the longer side = 5 × x = 5 × 8 = 40 cm
Question 14:
Mohan wants to buy a trapezium shaped field. Its side along the river is parallel and twice the side along the road. If the area of this field is 10500 m² and the perpendicular distance between the two parallel sides is 100 m, find the length of the side along the river.
ANSWER: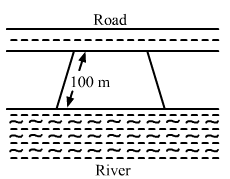
Given:Area of the trapezium shaped field = 10500 m²
It is also given that the length of the side along the river is double the length of the side along the road.
Let us suppose the length of the side along the road to be x.
Then, the length of the side along the river = 2 × x = 2x
And, the perpendicular distance between these parallel sides = 100 m
Area of trapezium = 1/2 × (Sum of the parallel sides) × (Perpendicular distance)
10500 = 1/2 × (2x + x) × (100)
10500 = 50 × (3x)
3x = 10500/50 = 210
x = 210/3 = 70 m
∴ Length of the side along the river = 2 × x = 2 × 70 = 140 m
PAGE NO 20.24:
Question 15:
The area of a trapezium is 1586 cm² and the distance between the parallel sides is 26 cm. If one of the parallel sides is 38 cm, find the other.
ANSWER:
Given:Area of the trapezium = 1586 cm²
Distance between the parallel sides = 26 cm
And, length of one parallel side = 38 cm
Let us suppose the length of the other side to be x cm.Now, area of the trapezium = 1/2 × (Sum of the parallel sides) × (Distance between the parallel sides)
⇒ 1586 = 1/2 × (38 + x) × (26)
⇒ 1586 = 26/2 × (38 + x)
⇒ 13 × (38 + x) = 1586
⇒ 38 + x = 1586/13 = 122
⇒ x = 122-38 = 84 cm
Hence, the length of the other parallel side is 84 cm.
Question 16:
The parallel sides of a trapezium are 25 cm and 13 cm; its nonparallel sides are equal, each being 10 cm, find the area of the trapezium.
ANSWER:
Given:The parallel sides of a trapezium are 25 cm and 13 cm.
Its nonparallel sides are equal in length and each is equal to 10 cm.
A rough sketch for the given trapezium is given below: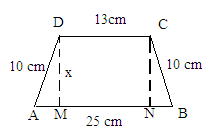
In above figure, we observe that both the right angle trangles AMD and BNC are congruent triangles.
AD = BC = 10 cm
D = CN = x cm
∠DMA = ∠CNB = 90°
Hence, the third side of both the triangles will also be equal.
∴AM = BN
Also, MN = 13
Since AB = AM + MN + NB:
∴ 25 = AM + 13 + BN
AM + BN = 25-13 = 12 cm
Or, BN + BN = 12 cm (Because AM = BN)
2 BN = 12
BN = 12/2 = 6 cm
∴ AM = BN = 6 cm.
Now, to find the value of x, we will use the Pythagoras theorem in the right angle triangle AMD, whose sides are 10, 6 and x.
(Hypotenuse)2 = (Base)2 + (Altitude)2
(10)2 = (6)2 + (x)2
100 = 36 + x2
x2 = 100-36 = 64
x = 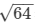 = 8 cm
= 8 cm
∴Distance between the parallel sides = 8 cm
∴ Area of trapezium = 1/2 × (Sum of parallel sides) × (Distance between parallel sides) = 1/2 × (25 + 13) × (8) = 152 cm²
Question 17:
Find the area of a trapezium whose parallel sides are 25 cm, 13 cm and the other sides are 15 cm each.
ANSWER:
Given:Parallel sides of a trapezium are 25 cm and 13 cm.
Its nonparallel sides are equal in length and each is equal to 15 cm.
A rough skech of the trapezium is given below: 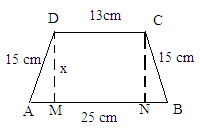
In above figure, we observe that both the right angle triangles AMD and BNC are similar triangles.This is because both have two common sides as 15 cm and the altitude as x and a right angle.Hence, the remaining side of both the triangles will be equal.
∴ AM = BN
Also MN = 13
Now, since AB = AM + MN + NB:
∴ 25 = AM + 13 + BN
AM + BN = 25-13 = 12 cm
Or, BN + BN = 12 cm (Because AM = BN)
2 BN = 12BN = 12/2 = 6cm
∴ AM = BN = 6 cm
Now, to find the value of x, we will use the Pythagorian theorem in the right angle triangle AMD whose sides are 15, 6 and x.
(Hypotenus)2 = (Base)2 + (Altitude)2
(15)2 = (6)2 + (x)2
225 = 36 + x2
x2 = 225−36 = 189
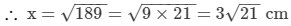
∴ Distance between the parallel sides = 3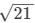 cm
cm
∴Area of trapezium = 12 × (Sum of parallel sides) × (Distance between the parallel sides)
= 12 × (25 + 13) × (3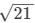 )
)
= 57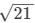 cm²
cm²
Question 18:
If the area of a trapezium is 28 cm² and one of its parallel sides is 6 cm, find the other parallel side if its altitude is 4 cm.
ANSWER:
Given:Area of the trapezium = 28 cm²
Length of one of its parallel sides = 6 cm
Altitude = 4 cm
Let the other side be x cm.Area of trapezium = 1/2 × (Sum of the parallel sides) × (Altitude)
⇒ 28 = 1/2 × (6 + x) × (4)
⇒ 28 = 2 × (6 + x)
⇒ 6 + x = 28/2 = 14
⇒ x = 14-6 = 8 cm
Hence, the length of the other parallel side of the trapezium is 8 cm.
Question 19:
In Fig. 20.38, a parallelogram is drawn in a trapezium, the area of the parallelogram is 80 cm², find the area of the trapezium.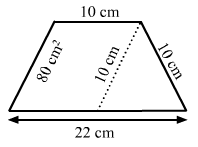
ANSWER:
The given figure is: The given figure is: 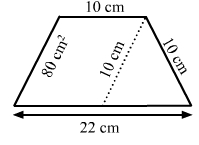
From above figure, it is clear that the length of the parallel sides of the trapezium are 22 cm and 10 cm.
Also, it is given that the area of the parallelogram is 80 cm² and its base is 10 cm.
We know:Area of parallelogram = Base × Height
∴ 80 = 10 × Height
Height = 80/10 = 8 cm
So, now we have the distance between the parallel sides of trapezium, which is equal to 8 cm.
∴ Area of trapezium = 1/2 × (Sum of the parallel sides) × (Distance between the parallel sides)
= 1/2 × (22 + 10) × (8) = 128 cm²
Question 20:
Find the area of the field shown in Fig. 20.39 by dividing it into a square, a rectangle and a trapezium.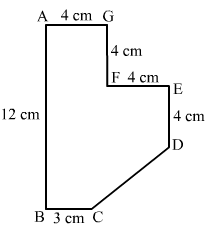
ANSWER:
The given figure can be divided into a square, a parallelogram and a trapezium as shown in following figure: 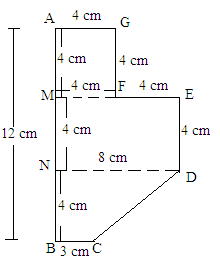
From the above figure:
Area of the figure = (Area of square AGFM with sides 4 cm) + (Area of rectangle MEDN with length 8 cm and width 4 cm)
+ (Area of trapezium NDCB with parallel sides 8 cm and 3 cm and perpendicular height 4 cm)
= (4 × 4) + (8 × 4) + [1/2 × (8 + 3) × (4)]
= 16 + 32 + 22
= 70 cm²
FAQs on Chapter 20 - Mensuration - I (Part - 2), Class 8, Maths RD Sharma Solutions - RD Sharma Solutions for Class 8 Mathematics
| 1. What is mensuration and why is it important in mathematics? |  |
| 2. How can I calculate the area of a triangle? |  |
| 3. What is the difference between perimeter and area? |  |
| 4. How do I calculate the volume of a rectangular prism? |  |
| 5. What is the relationship between radius and diameter of a circle? |  |

|
Explore Courses for Class 8 exam
|

|

















