Chapter 11 - Time and Work, Class 8, Maths RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics PDF Download
PAGE NO 11.10:
Question 1:
Rakesh can do a piece of work in 20 days. How much work can he do in 4 days?
ANSWER:
It is given that Rakesh can do a piece of work in 20 days.
∴ Rakesh's 1 day's work = 120
∴ Rakesh's work for 4 days = 4/20 = 1/5
Thus, he can do 1/5.th of the work in 4 days.
PAGE NO 11.10:
Question 2:
Rohan can paint 1/3 of a painting in 6 days. How many days will he take to complete the painting?
ANSWER:
Rohan can paint 1/3rd of a painting in 6 days.
∴ Time taken by Rohan to complete the painting = (6×3) days = 18 days.
PAGE NO 11.10:
Question 3:
Anil can do a piece of work in 5 days and Ankur in 4 days. How long will they take to do the same work, if they work together?
ANSWER:
Time taken by Anil to do the work = 5 days
Time taken by Ankur to do the work = 4 days
∴ Work done by Anil in 1 day = 1/5
Work done by Ankur in 1 day = 1/4
∴ Work done by Anil and Ankur in one day = 1/5 + 1/4
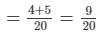
Thus, Anil and Ankur can do the work in 209 days i.e. 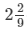 days.
days.
PAGE NO 11.10:
Question 4:
Mohan takes 9 hours to mow a large lawn. He and Sohan together can mow it in 4 hours. How long will Sohan take to mow the lawn if he works alone?
ANSWER:
Time taken by Mohan to do the work = 9 hours
Time taken by Mohan and Sohan to do the work = 4 hours
∴ Work done by Mohan = 1/9
Work done by Mohan and Sohan = 1/4
∴ Work done by Sohan = 1/4−1/9
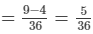
Thus, Sohan can do the work in 36/5 hours i.e. 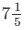 hours.
hours.
PAGE NO 11.10:
Question 5:
Sita can finish typing a 100 page document in 9 hours. Mita in 6 hours and Rita in 12 hours. How long will they take to type a 100 page document if they work together?
ANSWER:
Time taken by Sita to do the work = 9 hours
Time taken by Mita to do the work = 6 hours
Time taken by Rita to do the work = 12 hours
Now,Work done by Sita = 1/9
Work done by Mita = 1/6
Work done by Rita = 1/12
∴ Work done by them together = 1/9 + 1/6 + 1/12
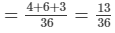
Thus, together they can do the work in 36/13 hours.
PAGE NO 11.10:
Question 6:
A, B and C working together can do a piece of work in 8 hours. A alone can do it in 20 hours and B alone can do it in 24 hours. In how many hours will C alone do the same work?
ANSWER:
Time taken by A to do the work = 20 hours
Time taken by B to do the work = 24 hours
Time taken by (A + B + C) to do the work = 8 hours
Now,Work done by A = 1/20
Work done by B = 1/24
Work done by (A + B + C) = 1/8
∴ Work done by C = 1/8−(1/20 + 1/24)
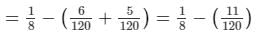
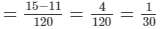
= 130
Thus, C can do the work in 30 hours.
PAGE NO 11.10:
Question 7:
A and B can do a piece of work in 18 days; B and C in 24 days and A and C in 36 days. In what time can they do it, all working together?
ANSWER:
Time taken by (A + B) to do the work = 18 days
Time taken by (B + C) to do the work = 24 days
Time taken by (A + C) to do the work = 36 days
Now,Work done by (A + B) = 1/18
Work done by (B + C) = 1/24
Work done by (A + C) = 1/36
∴ Work done together = (A + B) + (B + C) + (A + C)
= 1/18 + 1/24 + 1/36
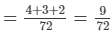
= 1/8
∴ Work done together = 2(A + B + C) = 1/8
∴ Work done by (A + B + C) = 1/16
Thus, together they can finish the work in 16 days.
PAGE NO 11.10:
Question 8:
A and B can do a piece of work in 12 days; B and C in 15 days; C and A in 20 days. How much time will A alone take to finish the work?
ANSWER:
Time taken by (A + B) to do the work = 12 days
Time taken by (B + C) to do the work = 15 days
Time taken by (A + C) to do the work = 20 days
Now,Work done by (A + B) = 1/12
Work done by (B + C) = 1/15
Work done by (A + C) = 1/20
∴ Work done together = (A + B) + (B + C) + (A + C)
= 1/12 + 1/15 + 1/20
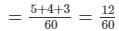
= 1/5
∴ Work done together = 2(A + B + C) = 1/5
∴ Work done by (A + B + C) = 1/10
∴ Work done by A alone = (A + B + C)−(B + C)
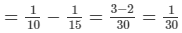
Thus, A alone can do the work in 30 days.
PAGE NO 11.10:
Question 9:
A, B and C can reap a field in 15341534 days; B, C and D in 14 days; C, D and A in 18 days; D, A and B in 21 days. In what time can A, B, C and D together reap it?
ANSWER:
Time taken by (A + B + C) to do the work = 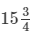 days = 6/34days
days = 6/34days
Time taken by (B + C + D) to do the work = 14 days
Time taken by (C + D + A) to do the work = 18 days
Time taken by (D + A + B) to do the work = 21 days
Now,Work done by (A + B + C) = 4/63
Work done by (B + C + D) = 1/14
Work done by (C + D + A) = 1/18
Work done by (D + A + B) = 1/21
∴ Work done by working together = (A + B + C) + (B + C + D) + (C + A + D) + (D + A + B)
= 4/63 + 1/14 + 1/18 + 1/21
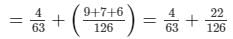
= 4/63 + 11/63 = 15/63
∴ Work done by working together = 3(A + B + C + D) = 15/63
∴ Work done by (A + B + C + D) = 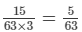
Thus, together they can do the work in 6/35 days or 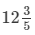 days.
days.
PAGE NO 11.10:
Question 10:
A and B can polish the floors of a building in 10 days. A alone can do 1/4th of it in 12 days. In how many days can B alone polish the floor?
ANSWER:
It is given that A and B can polish the floors of the building in 10 days.
∴ Work done by (A + B) in 1 day = 110
Now, A alone can do 14th of the work in 12 days.
∴ Time taken by A alone to do the complete work = (4×12) = 48 days
⇒ Work done by A in 1 day = 1/48
Now, work done by B in 1 day = Work done by (A + B) in 1 day −Work done by A in 1 day
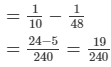
Thus, B alone can polish the floor in 240/19days or 12(12/19)days.
PAGE NO 11.10:
Question 11:
A and B can finish a work in 20 days. A alone can do 1515 th of the work in 12 days. In how many days can B alone do it?
ANSWER:
It is given that A and B can finish the work in 20 days.
∴ Work done by (A + B) in 1 day = 1/20
Now, A alone can do 15th of the work in 12 days.
∴ Time taken by A alone to complete the work = (5×12) = 60 days
⇒ Work done by A in 1 day = 1/60
Now, work done by B in 1 day = Work done by (A + B) in 1 day work−Work done by A in 1 day
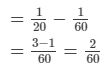
Thus, B alone can polish the floor in 60/2days or 30 days.
PAGE NO 11.10:
Question 12:
A and B can do a piece of work in 20 days and B in 15 days. They work together for 2 days and then A goes away. In how many days will B finish the remaining work?
ANSWER:
It is given that A can finish the work in 20 days and B can finish the same work in 15 days.
∴ Work done by A in 1 day = 1/20
Work done by B in 1 day = 1/15
∴ Work done by (A + B) in 1 day = 1/20 + 1/15
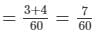
∴ Work done by (A + B) in 2 days = 14/60 = 7/30
Remaining work = 1−7/30 = 23/30
It is given that the remaining work is done by B.
∵ Complete work is done by B in 15 days.
∴ 23/30 of the work will be done by B in (15 × 23/30) days or 23/2 days or 11(1/2) days.
Thus, the remaining work is done by B in 11(1/2) days.
PAGE NO 11.10:
Question 13:
A can do a piece of work in 40 days and B in 45 days. They work together for 10 days and then B goes away. In how many days will A finish the remaining work?
ANSWER:
It is given that A can finish the work in 40 days and B can finish the same work in 45 days.
∴ Work done by A in 1 day = 1/40
Work done by B in 1 day = 1/45
∴ Work done by (A + B) in 1 day = 1/40 + 1/45

∴ Work done by (A + B) in 10 days = 10×17/360 = 17/36
Remaining work = 1−17/36 = 19/36
It is given that the remaining work is done by B.
Complete work is done by B in 45 days.
∴ 19/36 of the work will be done by B in (45 × 19/36) days or 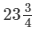 days.
days.
Thus, the remaining work is done by B in 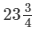 days.
days.
PAGE NO 11.10:
Question 14:
Aasheesh can paint his doll in 20 minutes and his sister Chinki can do so in 25 minutes. They paint the doll together for five minutes. At this juncture they have a quarrel and Chinki withdraws from painting. In how many minutes will Aasheesh finish the painting of the remaining doll?
ANSWER:
Aasheesh can paint a doll in 20 minutes, and Chinki can do the same in 25 minutes.
∴ Work done by Aasheesh in 1 minute = 1/20
∴ Work done by Chinki in 1 minute = 1/25
∴ Work done by them together = 1/20 + 1/25
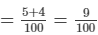
∴ Work done by them in 5 minutes = 5×9/100 = 9/20
Remaining work = 1−9/20 = 11/20
It is given that the remaining work is done by Aasheesh.
The work done by Aasheesh in 20 minutes.
∴ 11/20th work will be done by Aasheesh in (20×11/20) minutes or 11 minutes.
Thus, the remaining work is done by Aasheesh in 11 minutes.
PAGE NO 11.10:
Question 15:
A and B can do a piece of work in 6 days and 4 days respectively. A started the work; worked at it for 2 days and then was joined by B. Find the total time taken to complete the work.
ANSWER:
A can do a work in 6 days, and B can do the same work in 4 days.
∴ Work done by A in 2 days = 2/6 = 1/3
Remaining work = 1−1/3 = 2/3
∴ Work done by (A + B)in 1 day = (1/6 + 1/4)
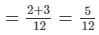
∵ 5/12th work is done by A and B in 1 day.
∴ 2/3rd work will be done by A and B in (1/25×2/3) days or 8/5 days.
∴ Total time taken = (8/5 + 2) days = 18/5 days = 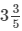 days
days
PAGE NO 11.10:
Question 16:
6 men can complete the electric fitting in a building in 7 days. How many days will it take if 21 men do the job?
ANSWER:
It is given that 6 men can complete a job in 7 days.
∴ Time taken by 1 man to complete the same job = (6×7) = 42 days
∴ Time taken by 21 men to complete the same job = 42/21 = 2 days
PAGE NO 11.10:
Question 17:
8 men can do a piece of work in 9 days. In how many days will 6 men do it?
ANSWER:
It is given that 8 men can complete a job in 9 days.
∴ Time taken by 1 man to complete the same job = (8×9) = 7/2 days
∴ Time taken by 6 men to complete the same job = 72/6 = 12 days
PAGE NO 11.10:
Question 18:
Reema weaves 35 baskets in 25 days. In how many days will she weave 55 baskets?
ANSWER:
It is given that Reema weaves 35 baskets in 25 days.
∴ Time taken by her to weave 1 basket = 25/35day
∴ Time taken by her to weave 55 baskets = (25/35×55) days
= 1375/35 days = 275/7 days
= 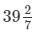 days
days
PAGE NO 11.10:
Question 19:
Neha types 75 pages in 14 hours. How many pages will she type in 20 hours?
ANSWER:
It is given that Neha types 75 pages in 14 hours.
∴ Number of pages typed by her in 1 hour = 75/14
∴ Number of pages typed by her in 20 hours
= (75/14×20) pages
= 1500/14 pages
= 750/7 pages =  pages
pages
Thus, Neha types 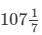 pages in 20 hours.
pages in 20 hours.
PAGE NO 11.10:
Question 20:
If 12 boys earn Rs 840 in 7 days, what will 15 boys earn in 6 days?
ANSWER:
Earnings of 12 boys in 7 days = Rs. 840
∴ Earnings of 12 boys in 1 day = Rs. 840/7 = Rs. 1/20
∴ Earnings of 1 boy in 1 day = Rs.120/12 = Rs. 10
∴ Earnings of 1 boy in 6 days = Rs. (10×6) = Rs. 60
∴ Earnings of 15 boys in 6 days = Rs.(60×15) = Rs. 900
PAGE NO 11.10:
Question 21:
If 25 men earn Rs 1000 in 10 days, how much will 15 men earn in 15 days?
ANSWER:
Earnings of 25 men in 10 days = Rs.1000
∴ Earnings of 25 men in 1 day = Rs.1000/10 = Rs.100
∴ Earning of 1 man in 1 day = Rs.100/25 = Rs.4
∴ Earnings of 1 men in 15 days = Rs.(15×4) = Rs.60
∴ Earnings of 15 men in 15 days = Rs.(60×15) = Rs. 900
PAGE NO 11.11:
Question 22:
Working 8 hours a day, Ashu can copy a book in 18 days. How many hours a day should he work so as to finish the work in 12 days?
ANSWER:
If Ashu works for 8 hours daily, he can finish the work in 18 days.
If he works for 1 hour daily, he can finish the work in (18×8) days or 144 days.
∴ Number of hours he should work daily to finish the work in 12 days = 144/12 = 12
PAGE NO 11.11:
Question 23:
If 9 girls can prepare 135 garlands in 3 hours, how many girls are needed to prepare 270 garlands in 1 hour?
ANSWER:
Number of garlands made by 9 girls in 1 hour = 135/3 = 45
Number of garlands made by 1 girl in 1 hour = 45/9 = 5
∴ Number of girls required to make 270 garlands in 1 hour = 270/5 = 54.
PAGE NO 11.11:
Question 24:
A cistern can be filled by one tap in 8 hours, and by another in 4 hours. How long will it take to fill the cistern if both taps are opened together?
ANSWER:
Time taken by the first tap to fill the cistern = 8 hours
Time taken by the second tap to fill the cistern = 4 hours
∴ Work done by the first tap in 1 hour = 1/8
Work done by the second tap in 1 hour = 1/4
∴ Work done by both the taps in 1 hour = 1/8 + 1/4

Thus, both the taps together will fill the cistern in 8/3 hours or 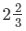 hours.
hours.
PAGE NO 11.11:
Question 25:
Two taps A and B can fill an overhead tank in 10 hours and 15 hours respectively. Both the taps are opened for 4 hours and they B is turned off. How much time will A take to fill the remaining tank?
ANSWER:
Pipe A can fill the tank in 10 hours, and pipe B can fill the tank in 15 hours.
∴ In 1 hour, A can fill 1/10th part of the tank.
In 1 hour, B can fill 1/15th part of the tank.
∴ In 1 hour, A and B can fill (1/10 + 1/15) 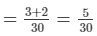 = 1/6th part of the tank
= 1/6th part of the tank
∴ In 4 hours, A and B can fill (1/6×4) = 2/3rd part of the tank
Remaining part of the tank = 1− 2/3 = 1/3
Now, A can fill the tank in 10 hours.
∴ 1/3rd part of the tank can be filled by A in (1/3×10) hours or 10/3 hours or  hours.
hours.
PAGE NO 11.11:
Question 26:
A pipe can fill a cistern in 10 hours. Due to a leak in the bottom it is filled in 12 hours. When the cistern is full, in how much time will it be emptied by the leak?
ANSWER:
When there is no leakage, the pipe can fill the cistern in 10 hours.
Thus, the pipe can fill 1/10th part of the cistern in 1 hour.
When there is leakage, the pipe can fill the cistern in 12 hours.
Therefore, in case of leakage, the pipe can fill 1/12th part of the cistern in 1 hour.
Thus, in one hour, due to leakge, (1/10−1/12)th or 1/60th part of the cistern is emptied.
Hence, the cistern will be emptied by the leakage in 60 hours.
PAGE NO 11.11:
Question 27:
A cistern has two inlets A and B which can fill it in 12 hours and 15 hours respectively. An outlet can empty the full cistern in 10 hours. If all the three pipes are opened together in the empty cistern, how much time will they take to fill the cistern completely?
ANSWER:
Time taken by tap A to fill the cistern = 12 hours
Time taken by tap B to fill the cistern = 15 hours
Let C be the outlet that can empty the cistern in 10 hours.
Time taken by tap C to empty the cistern = 10 hours
Now,Tap A fills 1/12th part of the cistern in 1 hour.
Tap B fills 1/15th part of the cistern in 1 hour.
Tap C empties out 1/10th part of the cistern in 1 hour.
Thus, in one hour, (1/12 + 1/15−1/10)th part of the cistern is filled.
We have:1/12 + 1/15−1/10 = 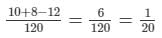
Thus, in 1 hour, 1/20th part of the cistern is filled.
Hence, the cistern will be filled completely in 20 hours if all the three taps are opened together.
PAGE NO 11.11:
Question 28:
A cistern can be filled by a tap in 4 hours and emptied by an outlet pipe in 6 hours. How long will it take to fill the cistern if both the tap and the pipe are opened together?
ANSWER:
Time taken by the tap to fill the cistern = 4 hours
∴ Tap fills 14th part of the cistern in 1 hour.
Time taken by the pipe to empty the cistern = 6 hours
∴ Pipe empties out 16th part of the cistern in 1 hour.
Thus, in 1 hour, (1/4−1/6)th part of the cistern is filled.
We have: 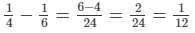
Thus, in 1 hour, 1/12th part of the cistern is filled.Hence, the cistern will be filled in 12 hours.
FAQs on Chapter 11 - Time and Work, Class 8, Maths RD Sharma Solutions - RD Sharma Solutions for Class 8 Mathematics
| 1. How can I solve time and work problems using the RD Sharma Solutions for Class 8 Maths? |  |
| 2. Can you provide an example of a time and work problem that can be solved using the RD Sharma Solutions for Class 8 Maths? |  |
| 3. Are there any shortcuts or tricks to solve time and work problems more quickly? |  |
| 4. Are there any real-life applications of time and work problems? |  |
| 5. Can you recommend any additional resources to practice time and work problems apart from RD Sharma Solutions for Class 8 Maths? |  |




















