Chapter 10 - Direct and Inverse Variations (Part - 1), Class 8, Maths RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics PDF Download
PAGE NO 10.6:
Question 1:
Explain the concept of direct variation.
ANSWER:
When two variables are connected to each other in such a way that if we increase the value of one variable, the value of other variable also increases and vice−versa.
Similarly, if we decrease the value of one variable, the value of other variable also decreases and vice−versa.
Therefore, if the ratio between two variables remains constant, it is said to be in direct variation.
PAGE NO 10.6:
Question 2:
Which of the following quantities vary directly with each other?
(i) Number of articles (x) and their price (y).
(ii) Weight of articles (x) and their cost (y).
(iii) Distance x and time y, speed remaining the same.
(iv) Wages (y) and number of hours (x) of work.
(v) Speed (x) and time (y) (distance covered remaining the same).
(vi) Area of a land (x) and its cost (y).
ANSWER:
(i) The number of articles is directly related to the price. Therefore, they will vary directly with each other.
(ii) The number of articles is directly related to the weight of the articles. Therefore, they will vary directly with each other.
(iii) Speed is constant. Therefore, distance and time does not vary directly.
(iv) The number of hours is directly related to the wages. Therefore, it is a direct variation.
(v) Distance is constant. Therefore, speed and time does not vary directly.
(vi) If the area of a land is large, its cost will also be high. Thus, it is a direct variation.
Thus, the respective values in (i), (ii), (iv) and (vi) vary directly with each other.
PAGE NO 10.6:
Question 3:
In which of the following tables x and y vary directly?
(i)
| a | 7 | 9 | 13 | 21 | 25 |
| b | 21 | 27 | 39 | 63 | 75 |
(ii)
| a | 10 | 20 | 30 | 40 | 46 |
| b | 5 | 10 | 15 | 20 | 23 |
(iii)
| a | 2 | 3 | 4 | 5 | 6 |
| b | 6 | 9 | 12 | 17 | 20 |
(iv)
| a | 12 | 22 | 32 | 42 | 52 |
| b | 13 | 23 | 33 | 43 | 53 |
ANSWER:
If x and y vary directly, the ratio of the corresponding values of x and y remains constant.
(i) x/y = 7/21 = 1/3
x/y = 9/27 = 1/3
x/y = 13/39 = 1/3
x/y = 21/63 = 1/3
x/y = 25/75 = 1/3
In all the cases, the ratio is the same. Therefore, x and y vary directly.
(ii) x/y = 10/5 = 2
x/y = 20/10 = 2
x/y = 30/15 = 2
x/y = 40/20 = 2
x/y = 46/23 = 2
In all the cases, the ratio is the same. Therefore, x and y vary directly.
(iii) x/y = 2/6 = 1/3
x/y = 3/9 = 1/3
x/y = 4/12 = 13
x/y = 5/17 = 517
x/y = 6/20 = 3/10
In all the cases, the ratio is not the same. Therefore, x and y do not vary directly.
(iv) x/y = 12/13 = 1
x/y = 22/23 = 1/2
x/y = 32/33 = 1/3
x/y = 42/43 = 1/4
x/y = 52/53 = 1/5
In all the cases, the ratio is not the same. Therefore, x and y do not vary directly.Thus, in (i) and (ii), x and y vary directly.
PAGE NO 10.6:
Question 4:
Fill in the blanks in each of the following so as to make the statement true:
(i) Two quantities are said to vary.... with each other if they increase (decrease) together in such a way that the ratio of the corresponding values remains same.
(ii) x and y are said to vary directly with each other if for some positive number k,...... = k.
(iii) If u = 3 v, then u and v vary .... with each other.
ANSWER:
(i) directly
(ii) x and y are said to vary directly with each other if x/y = k, where k is a positive number
(iii) because u = 3v, u and y vary directly with each other
PAGE NO 10.6:
Question 5:
Complite the following tables given that x varies directly as y.
(i)
| x | 2.5 | ... | ... | 15 |
| y | 5 | 8 | 12 | ... |
(ii)
| x | 5 | ... | 10 | 35 | 25 | ... |
| y | 8 | 12 | ... | ... | ... | 32 |
(iii)
| x | 6 | 8 | 10 | ... | 20 |
| y | 15 | 20 | ... | 40 | ... |
(iv)
| x | 4 | 9 | ... | ... | 3 | ... |
| y | 16 | ... | 48 | 36 | ... | 4 |
(v)
| x | 3 | 5 | 7 | 9 |
| y | ... | 20 | 28 | ... |
ANSWER:
Here, x and y vary directly.
∴ x = ky
(i) x = 2.5 and y = 5
i.e., 2.5 = k × 5
⇒ k = 2.5/5 = 0.5
For y = 8 and k = 0.5,
we have:x = ky
⇒ x = 8 × 0.5 = 4
For y = 12 and k = 0.5,
we have:x = ky
⇒ x = 12 × 0.5 = 6
For x = 15 and k = 0.5,
we have:x = ky
⇒ 15 = 0.5 × y
⇒ y = 15/0.5 = 30
(ii) x = 5 and y = 8
i.e., 5 = k × 8
⇒ k = 5/8 = 0.625
For y = 12 and k = 0.625,
we have:x = ky
⇒ x = 12 × 0.625 = 7.5
For x = 10 and k = 0.625,
we have:x = ky
⇒ 10 = 0.625 × y
⇒ y = 10/0.625 = 16
For x = 35 and k = 0.625,
we have:
x = ky
⇒ 35 = 0.625 × y
⇒ y = 35/0.625 = 56
For x = 25 and k = 0.625,
we have:x = ky
⇒ 25 = 0.625 × y
⇒ y = 25/0.625 = 40
For y = 32 and k = 0.625,
we have:
x = ky
⇒ x = 0.625 × 32 = 20
(iii) x = 6 and y = 15
i.e., 6 = k × 15
⇒ k = 6/15 = 0.4
For x = 10 and k = 0.4,
we have:y = 10/0.4 = 25
For y = 40 and k = 0.4,
we have:x = 0.4 × 40 = 16
For x = 20 and k = 0.4,
we have:y = 20/0.4 = 50
(iv) x = 4 and y = 16
i.e., 4 = k × 16
⇒ k = 4/16 = 1/4
For x = 9 and k = 1/4,
we have:9 = ky
⇒ y = 4 × 9 = 36
For y = 48 and k = 1/4, we have:
x = ky
= 1/4 × 48 = 12
For y = 36 and k = 1/4, we have:
x = ky
= 1/4 × 36 = 9
For x = 3 and k = 1/4, we have:
x = ky
⇒ 3 = 14 × y
⇒ y = 12
For y = 4 and k = 1/4, we have:
x = ky
= 1/4 × 4 = 1
(v) x = 5 and y = 20
i.e., 5 = k × 20
⇒ k = 5/20 = 1/4
For x = 3 and k = 1/4,
we have:3 = 1/4 × y
⇒ y = 4 × 3 = 12
For x = 9, k = 1/4, we have:
x = ky
⇒ 9 = 1/4 × y
⇒ y = 9 × 4 = 36
PAGE NO 10.7:
Question 6:
Find the constant of variation from the table given below:
| x | 3 | 5 | 7 | 9 |
| y | 12 | 20 | 28 | 36 |
Set up a table and solve the following problems. Use unitary method to verify the answer.
ANSWER:
Since it is a direct variation, x/y = k.
For x = 3 and y = 12,
we have:k = 3/12 = 1/4
Thus, in all cases, k = 1/4
PAGE NO 10.7:
Question 7:
Rohit bought 12 registers for Rs 156, find the cost of 7 such registers.
ANSWER:
Let the cost of 7 registers be Rs x.
| Register | 12 | 7 |
| Cost(in Rs.) | 156 | x |
If he buys less number of registers, the cost will also be less.
Therefore, it is a direct variation.We get:
12:7 = 156:x
⇒ 12/7 = 156/x
Applying cross muliplication, we get:x = 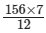
= 91
Thus, the cost of 7 such registers will be Rs 91.
PAGE NO 10.7:
Question 8:
Anupama takes 125 minutes in walking a distance of 100 metre. What distance would she cover in 315 minutes?
ANSWER:
Let the distance travelled in 315 minutes be x km.
| Time (in minute) | 125 | 315 |
| Distance(in metre) | 100 | x |
If the distance travelled is more, the time needed to cover it will also be more.
Therefore, it is a direct variation.We get:125:315 = 100:x
⇒ 125/315 = 100/x
Applying cross muliplication, we get:x = 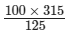
= 252
Thus, Anupama would cover 252 metre in 315 minutes.
PAGE NO 10.7:
Question 9:
If the cost of 93 m of a certain kind of plastic sheet is Rs 1395, then what would it cost to buy 105 m of such plastic sheet?
ANSWER:
| Length of plastic sheet (in metre) | 93 | 105 |
| Cost (in Rs) | 1395 | x |
Let the cost of the plastic sheet per metre be Rs x.
If more sheets are bought, the cost will also be more.Therefore, it is a direct variation.
We get:
93:105 = 1395:x
⇒ 93/105 = 1395/x
Applying cross muliplication, we get:x = 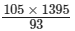
= 1575
Thus, the required cost will be Rs 1,575.
PAGE NO 10.7:
Question 10:
Suneeta types 1080 words in one hour. What is her GWAM (gross words a minute rate)?
ANSWER:
| Number of words | 1080 | x |
| Time (in minute) | 60 | 1 |
Let x be her GWAM.
If the time taken is less, GWAM will also be less.
Therefore, it is a direct variation.
1080:x = 60:1
⇒ 1080/x = 60/1
Applying cross muliplication, we get:x = 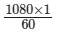
= 18
Thus, her GWAM will be 18.
PAGE NO 10.7:
Question 11:
A car is travelling at the average speed of 50 km/hr. How much distance would it travel in 12 minutes?
ANSWER:
| Distance (in km) | 50 | x |
| Time (in minute) | 60 | 12 |
Let the distance be x km.
If the time taken is less, the distance covered will also be less.
Therefore, it is a direct variation.
50:x = 60:12
⇒ 50/x = 60/12
Applying cross muliplication, we get:x =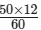
= 10
Thus, the required distance will be 10 km.
PAGE NO 10.7:
Question 12:
68 boxes of a certain commodity require a shelf-length of 13.6 m. How many boxes of the same commodity would occupy a shelf length of 20.4 m?
ANSWER:
| Number of Boxes | 68 | x |
| Shelf-length (in m) | 13.6 | 20.4 |
Let x be the number of boxes that occupy a shelf-length of 20.4 m.
If the length of the shelf increases, the number of boxes will also increase.
Therefore, it is a case of direct variation.
68/x = 13.6/20.4
⇒ 68 × 20.4 = x × 13.6
⇒ x = 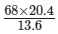
= 1387.2/13.6
= 102
Thus, 102 boxes will occupy a shelf−length of 20.4 m.
PAGE NO 10.7:
Question 13:
In a library 136 copies of a certain book require a shelf-length of 3.4 metre. How many copies of the same book would occupy a shelf-length of 5.1 metres?
ANSWER:
| Number of copies | 136 | x |
| Length the shelf (in m) | 3.4 | 5.1 |
Let x be the number of copies that would occupy a shelf-length of 5.1 m.
Since the number of copies and the length of the shelf are in direct variation,
we have:
136/x = 3.4/5.1
⇒ 136 × 5.1 = x × 3.4
⇒ x = 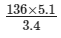
= 204
Thus, 204 copies will occupy a shelf of length 5.1 m.
PAGE NO 10.7:
Question 14:
The second class railway fare for 240 km of Journey is Rs 15.00. What would be the fare for a journey of 139.2 km?
ANSWER:
Let Rs x be the fare for a journey of 139.2 km.
| Distance (in km) | 240 | 139.2 |
| Fare (in Rs.) | 15 | x |
Since the distance travelled and the fare are in direct variation,
we have:
240/139.2 = 15/x
⇒ 240 × x = 15 × 139.2
⇒ x = 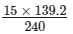
= 2088/240
= 8.7
Thus, the fare for a journey of 139.2 km will be Rs 8.70.
PAGE NO 10.7:
Question 15:
If the thickness of a pile of 12 cardboards is 35 mm, find the thickness of a pile of 294 cardboards.
ANSWER:
Let x cm be the thickness of a pile of 294 cardboards.
| Thickness (in cm) | 3.5 | x |
| Cardboard | 12 | 294 |
Since the pile of the cardboards and its thickness are in direct variation,
we have:
3.5/x = 12/294
⇒ 3.5 × 294 = x × 12
⇒ x = 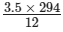
= 1029/12
= 85.75 cm
Thus, the thickness of a pile of 294 cardboards will be 85.75 cm (or 857.5 mm).
PAGE NO 10.7:
Question 16:
The cost of 97 metre of cloth is Rs 242.50. What length of this can be purchased for Rs 302.50?
ANSWER:
Let x metre be the length of the cloth that can be purchased for Rs 302.50.
| Length (in m) | 97 | x |
| Cost (in Rs) | 242.50 | 302.50 |
Since the length of the cloth and its cost are in direct variation, we have:
97/x = 242.50/302.50
⇒ 97 × 302.50 = x × 242.50
⇒ x = 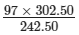
= 29342.50/242.50
= 121
Thus, the required length will be 121 metre.
PAGE NO 10.7:
Question 17:
11 men can dig 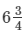 metre long trench in one day. How many men should be employed for digging 27 metre long trench of the same type in one day?
metre long trench in one day. How many men should be employed for digging 27 metre long trench of the same type in one day?
ANSWER:
Let x be the number of men required to dig a trench of 27 metre.
| Number of men | 11 | x |
| Length (in m) | 27/4 | 27 |
Since the length of the trench and the number of men are in direct variation,
we have:
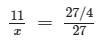
⇒ 11 × 27 = x × 27/4
⇒ x = 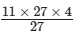
= 44
Thus, 44 men will be required to dig a trench of 27 metre.
PAGE NO 10.7:
Question 18:
A worker is paid Rs 210 for 6 days work. If his total income of the month is Rs 875, for how many days did he work?
ANSWER:
Let x be the number of days for which the worker is paid Rs 875.
| Income (in Rs.) | 210 | 875 |
| Number of days | 6 | x |
Since the income of the worker and the number of working days are in direct variation,
we have:
210/875 = 6/x
⇒ 210 × x = 875 × 6
⇒ x =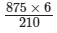
= 5250/210
= 25
Thus, the required number of days is 25.
PAGE NO 10.7:
Question 19:
A woker is paid Rs 200 for 8 days work. If he works for 20 days, how much will he get?
ANSWER:
Let Rs x be the income for 20 days of work.
| Income (in Rs) | 200 | x |
| Number of days | 8 | 20 |
Since the income and the number of working days are in direct variation, we have:
200/x = 8/20
⇒ 200 × 20 = 8x
⇒ x = 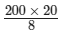
= 4000/8 = 500
Thus, the worker will get Rs 500 for working 20 days.
PAGE NO 10.7:
Question 20:
The amount of extension in an elastic string varies directly as the weight hung on it. If a weight of 150 gm produces an extension of 2.9 cm, then what weight would produce an extension of 17.4 cm?
ANSWER:
Let x gm be the weight that would produce an extension of 17.4 cm.
| Weight (in gm) | 150 | x |
| Length (in cm) | 2.9 | 17.4 |
Since the amount of extension in an elastic string and the weight hung on it are in direct variation, we have:
150/x = 2.9/17.4
⇒ 17.4 × 150 = 2.9 × x
⇒ x = 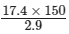
= 2610/2.9
= 900
Thus, the required weight will be 900 gm.
PAGE NO 10.8:
Question 21:
The amount of extension in an elastic spring varies directly with the weight hung on it. If a weight of 250 gm produces an extension of 3.5 cm, find the extension produced by the weight of 700 gm.
ANSWER:
Let x cm be the extension produced by the weight of 700 gm.
| Weight (in gm) | 250 | 700 |
| Length (in cm) | 3.5 | x |
Since the amount of extension in an elastic spring varies and the weight hung on it is in direct variation, we have:
250/700 = 3.5/x
⇒ x × 250 = 3.5 × 700
⇒ x = 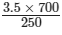
= 2450/250 = 9.8
Thus, the required extension will be 9.8 cm.
PAGE NO 10.8:
Question 22:
In 10 days, the earth picks up 2.6 × 108 pounds of dust from the atmosphere. How much dust will it pick up in 45 days?
ANSWER:
Let the amount of dust picked up by the earth in 45 days be x pounds.
Since the amount of dust picked up by the earth and the number of days are in direct variation,
we have:
Ratio of the dust picked up by the earth in pounds = ratio of the number of days taken
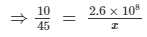
⇒ x × 10 = 45 × 2.6 × 108
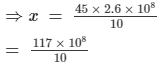
= 11.7 × 108
Thus, 11.7×108 pounds of dust will be picked up by the earth in 45 days.
PAGE NO 10.8:
Question 23:
In 15 days, the earth picks up 1.2 × 108 kg of dust from the atmosphere. In how many days it will pick up 4.8 × 108 kg of dust?
ANSWER:
Let x be the number of days taken by the earth to pick up 4.8×108 kg of dust.
Since the amount of dust picked up by the earth and the number of days are in direct variation,
we get:
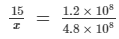
⇒ x = 15 × 4.8/1.2
⇒ x = 60
Thus, the required number of days will be 60.
FAQs on Chapter 10 - Direct and Inverse Variations (Part - 1), Class 8, Maths RD Sharma Solutions - RD Sharma Solutions for Class 8 Mathematics
| 1. What is direct variation and inverse variation in mathematics? |  |
| 2. How can we identify direct variation and inverse variation from a given equation or graph? |  |
| 3. What are some real-life examples of direct variation and inverse variation? |  |
| 4. Can there be situations where both direct variation and inverse variation occur simultaneously? |  |
| 5. How can we solve problems involving direct and inverse variations? |  |

|
Explore Courses for Class 8 exam
|

|

















