Chapter 2 - Powers (Ex-2.2) Part- 2 Class 8 Math RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics PDF Download
Question 8: By what number should (−5) −1 be multiplied so that the product is (−8) −1
Answer 8:
Let the number be x.
According to the question, 



Question 9: By what number should (15) −1 be multiplied so that the product may be equal to (−5) −1 ?
Answer 9:
Let the required number be x.
Therefore,

x=−3
Hence, the required number is −3.
Question 10:
By what number should (−15)−1 be divided so that the quotient may be equal to (−5)−1?
Answer 10:
Expressing in fractional form, we get:
(−15)−1 = −1/15, ---> (a−1 = 1/a)
and
(−5)−1 = −1/5 ---> (a−1 = 1/a)
We have to find a number x such that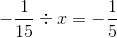 Solving this equation, we get:
Solving this equation, we get:
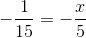
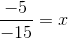
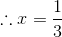 Hence, (−15)−1 should be divided by 1/3 to obtain (−5)−1.
Hence, (−15)−1 should be divided by 1/3 to obtain (−5)−1.
Question 11:
By what number should (5/3)−2 be multiplied so that the product may be (73)−1?
Answer 11:
Expressing as a positive exponent, we have: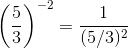 ---> (a−1 = 1/a)
---> (a−1 = 1/a) 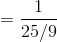 ---> ((a/b)n = (an)/(bn))
---> ((a/b)n = (an)/(bn)) 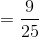 and(7/3)−1 = 3/7. ---> (a−1 = 1/a)
and(7/3)−1 = 3/7. ---> (a−1 = 1/a)
We have to find a number x such that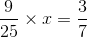 Multiplying both sides by 25/9, we get:
Multiplying both sides by 25/9, we get: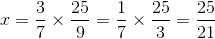 Hence, (5/3)−2 should be multiplied by 25/21 to obtain (7/3)−1.
Hence, (5/3)−2 should be multiplied by 25/21 to obtain (7/3)−1.
Question 12:
Find x, if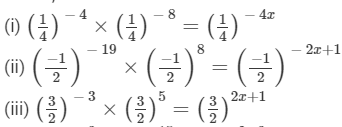

Answer 12:
(i) We have:
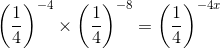
 (am×an = am+n)
(am×an = am+n)
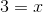
x = 3
(ii) We have:
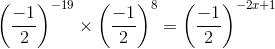
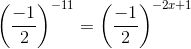 (am×an = am+n)
(am×an = am+n)

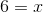
x = 6
(iii) We have:
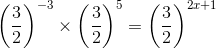
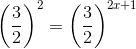
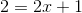

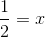
x = 1/2
(iv) We have:
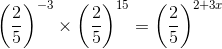
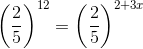
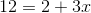

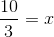
x = 10/3
(v) We have:
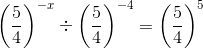

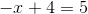
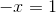

(vi) We have:
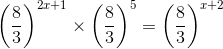
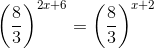


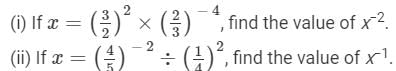
(i) First, we have to find x.
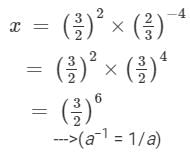 x = 322×23-4 = Hence, x−2 is:
x = 322×23-4 = Hence, x−2 is: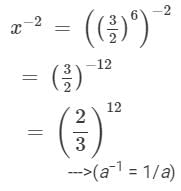
(ii) First, we have to find x.
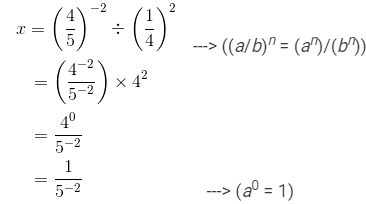
Hence, the value of x−1 is:
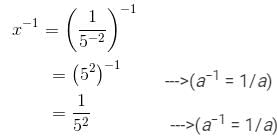
Question 14: Find the value of x for which 52x ÷ 5−3 = 55.
Answer 14:
We have: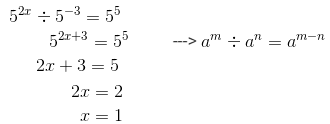
hence, x is 1.
FAQs on Chapter 2 - Powers (Ex-2.2) Part- 2 Class 8 Math RD Sharma Solutions - RD Sharma Solutions for Class 8 Mathematics
| 1. How do you find the value of a number raised to a power? |  |
| 2. What is the meaning of a negative exponent? |  |
| 3. How do you simplify expressions with exponents? |  |
| 4. What is the difference between the exponent and the base of a power? |  |
| 5. How are powers used in real-life applications? |  |















