Short & Long Answer Questions: System of Particles & Rotational Motion - 2 | Physics for EmSAT Achieve PDF Download
Q.51 Why is it more difficult to revolve a stone tied to a large string than a stone tied to a smaller string?
Answer: The length of the string increases the distance of rotating mass from the axis of rotation and hence moment of inertia of the system is increased. Now, τ=Iαa thus a system with large moment of inertia requires large torque for its rotation.
Q.52 Two satellites of equal masses, which can be considered as particles are orbiting the earth at different heights? Will their moments of inertia be same or different?
Answer: M.I. of a satellite, I=Mr2 i.e., I ∝ r2 Hence the two satellites orbiting the earth at different heights will have different moments of inertia. The satellite orbiting at a larger height will have a larger moment of inertia.
Q.53 What is the use of flywheel in railway engine?
Answer: In a flywheel, most of the mass is concentrated at its rim. So it has a large moment of inertia. Any change of angular momentum imparted to the wheel by the piston results in a lesser change of angular velocity(L=Iω or ω=L/I ). Moreover, a flywheel stores a large amount of rotational energy(1/2 Iω2). This helps the wheel c fly off the dead point.
Q.54 There is a stick half of which is wooden is and half is of steel. It is pivoted at the wooden end and a force is applied at the steel end at right angles to its length. Next, it is pivoted at the steel end and the same force is applied at the wooden end. In which case is the angular acceleration more and why?
Answer: The distribution of mass is farther from the axis of rotation in the first case than in the second case. So the moment of inertia is more in first case than in second case, but the applied torque τ is same in both cases. Asτ=Iα or α=τ/I,, so the angular acceleration α is less in first case than in second case.
Q.55 Is the angular momentum of a system always conserved? If not, under what condition is it conserved?
Answer: No, angular momentum of a system is not always conserved. It is conserved only when no external torque acts on the system.
Q.56 A flywheel is revolving with a constant angular velocity. A chip of its rim breaks and flies away. What will be the effect on its angular velocity?
Answer: Due to the decrease in its mass, the moment of inertia of the flywheel will decrease. To conserve angular momentum, the angular velocity of the flywheel will increase.
Q.57 A cat is able to land on its feet after a fall. Why?
Answer: When a cat falls to ground from a height, it stretches its body along with the tail so that its moment of inertia becomes high. Since Iω is to remain constant, the value of angular speed ω decreases and therefore the cat is able to land on the ground gently.
Q.58 Why there are two propellers in a helicopter?
Answer: If there were only one propeller in the helicopter then, due to conservation of angular momentum, the helicopter itself would have turned in the opposite direction.
Q.59 The speed of a whirl wind in a tornado is alarmingly high. Why?
Answer: In a whirl wind, the air from nearby region gets concentrated in a small space thereby decreasing the value of moment of inertia considerably. Since, Iω=constant, due to decrease in moment of inertia, the angular speed becomes quite high.
Q.60 If earth contracts to half its radius, what would be the length of the day?
Answer: The moment of inertia (I=2/5 MR2) of the earth about its own axis will become one fourth and so its angular velocity will become four times L=Iω= constant). Hence the time period will reduce to one fourth (T=2π/ω)i.e., 6 hours.
Q.61 Two boys of the same weight sit at the opposite ends of a diameter of a rotating circular table. What happens to the speed of rotation if they move nearer to the axis of rotation?
Answer: The moment of inertia of the system /circular table + two boys) decreases. To conserve angular momentum (L=Iω=constant), the speed of rotation of the circular table increases.
Q.62 A thin wheel can stay up right on its rim for a considerable length of time when rolled with a considerable velocity, while it falls from its upright position at the slightest disturbance when stationary. Give reason.
Answer: When the wheel is rolling upright, it has angular momentum in the horizontal direction i.e., along the axis of the wheel. Because the angular momentum is to remain conserved, the wheel does not fall from its upright position because that would change the direction of angular momentum. The wheel falls only when it loses its angular velocity due to friction.
Q.63 A person is standing on a rotating table with metal spheres in his hands. If he withdraws his hands to his chest, what will be the effect on his angular velocity?
Answer: When the person withdraws his hands to his chest, his moment of inertia decreases. No external torque is acting on the system. So to conserve angular momentum, the angular velocity increases.
Q.64 A circular turn table rotates at constant angular velocity about a vertical axis. There is no friction and no driving torque. An ice pan containing ice also rotates with it. The ice melts but none of the water escapes from the pan. Is the velocity now greater, the same or less than the original velocity? Give reason.
Answer: Due to accumulation of water near the edge, the moment of inertia of the system increases. To conserve angular momentum, the angular velocity of the system decreases.
Q.65 Many rivers flow towards the equator. What effect does the sediment they carry to the seas have on the rotation of the earth?
Answer: The rivers carry sediments away from the axis of rotation of the earth. This increases the rotational inertia the earth. To conserve angular momentum, the rotational speed of the earth decreases.
Q.66 The moments of inertia of two rotating bodies A and B are IA and IB(IA>IB)and their angular momenta are equal. Which one has a greater kinetic energy?
Answer: Angular momentum, L=Iω K.E. of rotation, 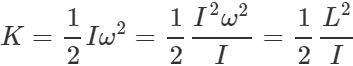 For constant L, K ∝ 1/I. As IA>IB ∴ KA<KB or KB>KA. So body B has a greater rotational K.E.
For constant L, K ∝ 1/I. As IA>IB ∴ KA<KB or KB>KA. So body B has a greater rotational K.E.
Q.67 If angular momentum is conserved in a system whose moment of inertia is decreased, will its rotational kinetic energy be conserved?
Answer: Here L=Iω=constant Rotational K.E. is given by 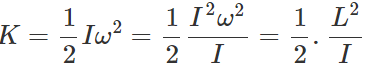 For constant L, K ∝ 1/I So when the moment of inertia decreases, the rotational K.E. increases. Hence rotational K.E. is not conserved.
For constant L, K ∝ 1/I So when the moment of inertia decreases, the rotational K.E. increases. Hence rotational K.E. is not conserved.
Q.68 How does an ice-skater, a ballet dancer or an acrobat take advantage of the principle of conservation of angular momentum?
Or
How does a ballet dancer vary her angular speed by outstretching her arms and legs?
Answer: An ice-skater, a ballet dancer or an acrobat is able to change his angular speed during the course of the performance. When the performer stretches out his hands and legs, his moment of inertia increases and the angular speed decreases. On the other hand, when he folds his hands and the legs near his body, the moment of inertia decreases and he is able to increase the angular speed.
Q.69 If earth were to shrink suddenly, what would happen to the length of the day?
Answer: When the earth shrinks, the moment of inertia 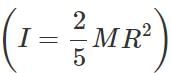 decreases about its own axis due to the decrease in radius R To conserve angular momentum.
decreases about its own axis due to the decrease in radius R To conserve angular momentum.
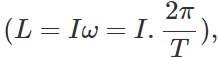 the time period T decreases. That is, the length of the day decreases.
the time period T decreases. That is, the length of the day decreases.
Q.70 A body A of mass M while falling vertically downwards under gravity breaks into two parts; a body B of mass M/ 3 and a body C of mass 2 M/ 3. How does the centre of mass of bodies B and C taken together shift compared to that of A?
Answer: The centre of mass of bodies B and C does not shift compared to body A. It continues to move vertically downwards under the effect of gravity. This is because there is no new external force acting on the system.
Q.71 Two identical particles move towards each other with velocity 2υ and υ respectively. What is the velocity of the centre of mass?
Answer: Here m1=m2=m; υ=2υ and υ2=−υ ∴ 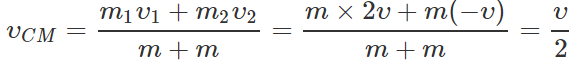
Q.72 A particle moves in a circular path with decreasing speed. What happens to its angular momentum?
Answer: The angular momentum of a particle of mass m moving with velocity 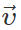 along a circular path of radius r is given by
along a circular path of radius r is given by 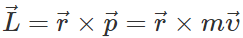 When the speed υ decreases, the magnitude of angular momentum decreases. But the direction of angular momentum remains unchanged.
When the speed υ decreases, the magnitude of angular momentum decreases. But the direction of angular momentum remains unchanged.
Q.73 A particle performing uniform circular motion has angular momentum L. What will be the new angular momentum, if its angular frequency is doubled and its kinetic energy halved?
Answer: Rotational K.E., K= 1/2 Iw2 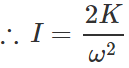 Angular momentum,
Angular momentum,
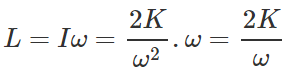 When angular frequency is doubled and kinetic energy is halved, the angular momentum becomes,
When angular frequency is doubled and kinetic energy is halved, the angular momentum becomes, 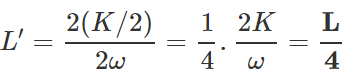
Q.74 The angular velocity of the earth around the sun increases, when it comes closer to the sun. Why?
Answer: When the earth comes closer to the sun, its moment of inertia about the axis through the sun decreases. To conserve angular momentum(L=Iω), the angular velocity of the earth increases.
Q.75 Why are we not able to rotate a wheel by pulling or pushing along its radius?
Answer: This is because radial component of the applied force cannot produce torque. τ = r F sinθ = 0 × Fsin θ = 0
Q.76 Two solid spheres of the same mass are made of metals of different densities. Which of them has larger moment of inertia about its diameter?
Answer: The sphere of metal with smaller density, will have larger size and hence it will have larger moment of inertia than the other sphere.
Q.77 A planet revolves around a massive star in a highly elliptical orbit. Is the angular momentum constant over the entire orbit?
Answer: A planet revolves around a star under the effect of the gravitational force, which is purely radial in nature. As radial component of a force does not contribute to torque, so the angular momentum of the planet remains unaffected. As τ=dL/dt=0, so L=constant.
Q.78 If no external torque acts on a body, will its angular velocity remain constant? Give reason.
Answer: When no external torque acts on a body, its angular momentum remains constant. But L=Iω Clearly, the angular velocity ω will remain constant only so long as the moment of inertia I of the body remains constant.
Q.79 "Newton's laws of motion are applicable to individual particles". How would you explain the motion of a large body?
Answer: A large body can be considered as made of a number of mass particles and all mass particles interact with each other. The vector sum of all these internal forces is zero. Therefore for a large body, it can be replaced by a single mass particle whose mass is supposed to be situated at its centre of mass and the Newton's laws can be applied.
Q.80 If an external force can change the state of motion of CM of a body, how does the internal force of the brakes bring a car to rest?
Answer: Actually, it is not the external force which brings the car to rest. The internal force of the brakes on the wheel locks the wheel. Now a large frictional force comes into play between the wheels and the grounds. This force is external to the system and brings the car to rest.
Q.81 Two men stand facing each other on two boats floating on still water at a distance apart. A rope is held at its ends by both. The two boats are found to meet always at the same point, whether each man pulls separately or both pull together, why? Will the time taken be different in the two cases? Neglect friction.
Answer: The men on the two boats floating on water constitute a single system. So the forces applied by the two men are internal forces. Whether each man pulls separately or both pull together, the centre of mass of the system of boats remains fixed due to the absence of any external force. Consequently, the two boats meet at a fixed point, which is the centre of mass of the system.
Q.82 What is the difference between centre of gravity and centre of mass?
Answer: Centre of mass is a point at which whole of the mass of the body may be assumed to be concentrated to describe its motion as a particle. Centre of gravity is a point at which resultant of the gravitational forces on all particles of the body acts. For bodies of normal dimensions, centre of mass and centre of gravity coincide. But centre of mass and centre of gravity relate to two different concepts. Even if the world were devoid of gravitational force, the centre of mass would still have a meaning.
Q.83 There are 100 passengers in a stationary railway compartment. A physical fight starts between the passengers over some difference of opinion, (i) Will the position of CM of the compartment change? (ii) Will the position of CM of system (compartment +100 passengers) change? Give reason.
Answer: (i) The position of the CM of the compartment will change because the passengers are external bodies for the compartment. (ii) The position of CM of the system will not change as no external force is acting on the system.
Q.84 Torque and work are both equal to force times distance. Then how do they differ?
Answer: (i) Work is a scalar quantity while torque is a vector quantity. (ii) Work is measured as the product of the applied force and the distance moved by the body in the direction of the force. Torque is measured as the product of the force and its perpendicular distance from the axis of rotation.
Q.85 When is a rigid body said to be in equilibrium? State the necessary conditions for a body to be in equilibrium.
Answer: A rigid body is said to be in equilibrium when its linear acceleration and angular acceleration are zero. (i) For translation equilibrium of a rigid body, the sum of all the external forces acting on it must be zero 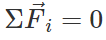 (ii) For rotational equilibrium of a rigid body, the sum of torques due to all forces acting on it must be zero.
(ii) For rotational equilibrium of a rigid body, the sum of torques due to all forces acting on it must be zero. 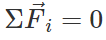
Q.86 Define moment of inertia. On what factors does it depend?
Answer: The moment of inertia of a rigid body about' an axis is the sum of the products of the masses of its various particles and squares of their perpendicular distances from the axis of rotation. I=Σmir2i The moment of inertia of a body depends on:-
(i) Mass of the body.
(ii) Size and shape of the body.
(iii) Distribution of mass about the axis of rotation.
(iv) Position and orientation of the axis of rotation with respect to the body.
Q.87 How will you distinguish between a hard boiled egg and a raw egg by spinning it on a table top?
Answer: Hard boiled egg acts just like a rigid body while rotating while it is not the case in a raw egg because of liquid matter present in it. In case of a raw egg, the liquid matter tries to go away from the centre, thereby increasing its moment of inertia. As moment of inertia is more the raw egg will spin with less angular acceleration provided same torque is applied in both the cases. Thus, hard boiled egg will spin faster.
Q.88 If two circular discs of the same mass and thickness are made from metals of different densities, which disc will have the larger moment of inertia about its central axis ? Explain.
Answer: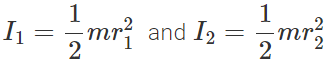
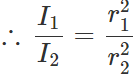 Also
Also 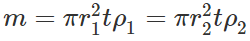
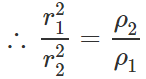 Hence
Hence 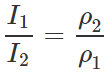 i.e., I∝1/ρ Thus the disc with greater density will have less moment of inertia.
i.e., I∝1/ρ Thus the disc with greater density will have less moment of inertia.
Q.89 Which one is easier to turn-a log or a bench of equal weight and length? The two have the same coefficient of friction with the ground. Explain.
Answer: In the case of a log, the force of friction is distributed along its entire length and so it is effective midway between the end where the force is applied and the centre of the log, but in the case of a bench, the force of friction is at the end. So to turn the log, the torque required is equal to μ mg l/2,, while to turn the bench, the torque required is equal to μ mgl. Hence it is easier to turn a log than a bench of equal weight and length.
Q.90 What is the moment of inertia of a rod of mass M, length l about an axis perpendicular to it through one end? Given the moment of inertia about the centre of mass is 1/12 Ml2
Answer: By using theorem of parallel axes, 
Q.91 What is the moment of inertia of a uniform circular disc of radius R and mass M about an axis passing through its centre and normal to the disc? The moment of inertia of the disc about any of its diameters is given to be(1 / 4) MR2.
Answer: M.I. of the disc about any diameter, ID=1/4MR2. By the theorem of perpendicular axes, M.I of the disc about an axis through the centre and normal to disc = M.I about any diameter+M.I about perpendicular diameter 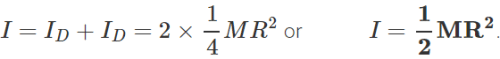
Q.92 The moment of inertia of a solid sphere about a tangent is 5/3 MR2, where M is mass and R is radius of the sphere. Find the M.I. of the sphere about its diameter.
Answer: Here IT=5/3 MR2 Now diameter of sphere is an axis passing through its centre of mass. By using theorem of parallel axes, IT=ICM+MR2 ∴
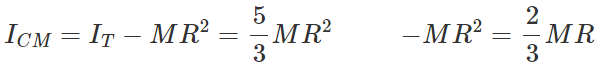
Q.93 The moment of inertia of a uniform circular disc about a tangent in its own plane is 5/4 MR2, where M is mass and R is the radius of the disc. Find its moment of inertia about an axis through its centre and perpendicular to its plane.
Answer: If ID is the M.I. of the disc about its diameter, then from the theorem of parallel axes, IT=ID+MR2 or ID=IT−MR2=5/4 MR2 −MR2=1/4 MR2 By the theorem of perpendicular axes, the M.I. about an axis through the centre and perpendicular to the plane of the disc, I= Sum of moments of inertia about two perpendicular diameters =ID+ID=2×1/4 MR2 or I=1/2 MR2.
Q.94 Using expressions for power and kinetic energy of rotational motion, derive the relation. τ=Iα,, where letters have their usual meanings.
Answer: Power in rotational motion, P=τω Rotational K.E., K=1/2 Iω2 Work done in rotational motion, W=Energy stored as rotational K.E. =1/2 Iω2 ∴ 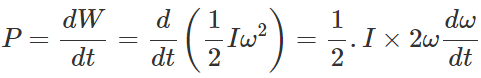 or τω=Iωα
or τω=Iωα
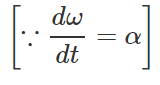 ∴ τ=Iα.
∴ τ=Iα.
Q.95 Explain if the ice on the polar caps of the earth melts, how will it affect the duration of the day?
Answer: If the ice on the polar caps of the earth melts, the water so formed will spread on the surface of earth. This increases the moment of inertia (I) of the earth about its own axis (due to change in the distribution of mass of the particles of water going away from the axis of rotation). To conserve angular momentum (=Iω), co (angular velocity of earth about its own axis) will decrease. As T=2π/ω,, hence due to decrease in the value of ω, T i.e., the duration of the day will increase.
Q.96 Two identical cylinders 'run a race' starting from rest at the top of an inclined plane, one slides without rolling and other rolls without slipping. Assuming that no mechanical energy is dissipated as heat, which one will win?
Answer: When the cylinder slides without rolling, E=1/2mυ′2 ∴
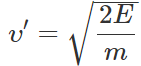 When the cylinder rolls without slipping,
When the cylinder rolls without slipping,

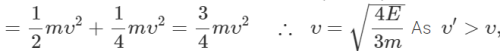 therefore sliding cylinder will win the race.
therefore sliding cylinder will win the race.
|
208 videos|230 docs|191 tests
|
FAQs on Short & Long Answer Questions: System of Particles & Rotational Motion - 2 - Physics for EmSAT Achieve
| 1. What is the difference between linear motion and rotational motion? |  |
| 2. How is the moment of inertia different from mass? |  |
| 3. What is torque and how is it related to rotational motion? |  |
| 4. How does the distribution of mass affect the rotational motion of an object? |  |
| 5. What is angular momentum and how is it conserved in rotational motion? |  |

|
Explore Courses for EmSAT Achieve exam
|

|

















