Double Slit Experiment | Physics Class 12 - NEET PDF Download
Conditions for Interference-: Observable interference can take place if the following conditions are fulfilled:
(a) The two sources should emit, continuously, waves of some wave-length or frequency. While deriving conditions for maxima and minima, we have taken ‘I’ for both the waves to be same.
(b) The amplitudes of the two waves should be either or nearly equal. A good contrast between a maxima and minima can only be obtained if the amplitudes of two waves are equal or nearly equal.
(c) The two sources should be narrow. A broader source can be supposed to be a combination of a number of narrow sources assembled side-by-side. Interference patterns due to these narrow sources may overlap each other.
(d) The sources should be close to each other. The fringe width varies inversely as distance ‘d’ between the two sources. So, interference pattern will be more clear and distant if ‘d’ is small.
(e) The two sources should be coherent one.
Double Slit Experiment-: The phenomenon of interference was first observed and demonstrated by Thomas Young in 1801. The experimental set up is shown in figure.
Light from a narrow slit S, illuminated by a monochromatic source, is allowed to fall on two narrow slits A and B placed very close to each other. The width of each slit is about 0.03 mm and they are about 0.3 mm apart. Since A and B are equidistant from S, light waves from S reach A and B in phase. So A and B acts as coherent sources.
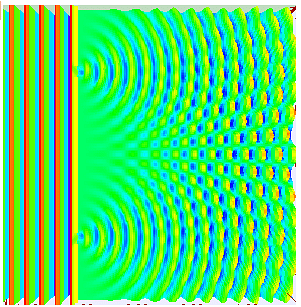
According to Huygen’s principle, wavelets from A and B spread out and overlapping takes place to the right side of AB. When a screen XY is placed at a distance of about 1 meter from the slits, equally spaced alternate bright and dark fringes appear on the screen. These are called interference fringes or bands. Using an eyepiece the fringes can be seen directly. At P on the screen, waves from A and B travel equal distances and arrive in phase. These two waves constructively interfere and bright fringe is observed at P. This is called central bright fringe.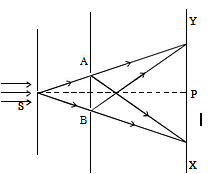
When one of the slits is covered, the fringes disappear and there is uniform illumination on the screen. This shows clearly that the bands are due to interference.
Let d be the distance between two coherent sources A and B of wavelength λ. A screen XY is placed parallel to AB at a distance D from the coherent sources. C is the midpoint of AB. O is a point on the screen equidistant from A and B. P is a point at a distance x from O, as shown in Fig 5.17. Waves from A and B meet at P in phase or out of phase depending upon the path difference between two waves
Draw AM perpendicular to BP
The path difference δ = BP – AP
AP = MP
δ = BP – AP = BP – MP = BM
In right angled ? ABM, BM = d sin θ If θ is small,
sin θ = θ
The path difference δ = θ.d
In right angled triangle COP, tan θ = OP/CO = x/D
For small values of θ, tan θ = θ
Thus, the path difference δ = xd/D
Bright Fringes
By the principle of interference, condition for constructive interference is the path difference = nλ
xd/D = nλ
Here, n = 0,1,2.....indicate the order of bright fringes
So, x = (D/d) nλ
This equation gives the distance of the nth bright fringe from the point O.
Bright Fringes
By the principle of interference, condition for constructive interference is the path difference = nλ
xd/D = nλ
Here, n = 0,1,2.....indicate the order of bright fringes
So, x = (D/d) nλ
This equation gives the distance of the nth bright fringe from the point O.
Dark Fringes
By the principle of interference, condition for destructive interference is the path difference = (2n-1)λ/2
Here, n = 1,2,3 … indicate the order of the dark fringes.
So, x = (D/d) [(2n – 1)λ/2]
This equation gives the distance of the nth dark fringe from the point O. Thus, on the screen alternate dark and bright bands are seen on either side of the central bright band.
Band Width (β)
The distance between any two consecutive bright or dark bands is called bandwidth.
The distance between (n+1)th and nth order consecutive bright fringes from O is given by,
xn+1 – xn = [(D/d) [(n+1)λ] – (D/d) [(n)λ]] = (D/d) λBandwidth, β = (D/d) λ
Similarly, it can be proved that the distance between two consecutive dark bands is also equal to (D/d) λ. Since bright and dark fringes are of same width, they are equi−spaced on either side of central maximum.
Condition for Obtaining Clear and Broad Interference Bands
The screen should be as far away from the source as possible.
The wavelength of light used must be larger.
The two coherent sources must be as close as possible.
The interference pattern in which the positions of maximum and minimum intensity of light remain fixed with time, is called sustained or permanent interference pattern. The conditions for the formation of sustained interference may be stated as :
(a) The two sources should be coherent
(b) Two sources should be very narrow
(c) The sources should lie very close to each other to form distinct and broad fringes.
Did You Know?
- The waves must be of the same type and must meet at a point.
- The waves must be both either unpolarised or have the same plane of polarisation.
- The dark and light regions are called interference fringes, the constructive and destructive interference of light waves.
- Interference fringes consisting of alternately bright and dark fringes (or bands) which are equally spaced are observed
- The distance D (from the double slits to the screen) is very much greater than d, typically ~ 1 m.
- The fringe separation Δx is increased if distance to the screen D is increased.
- The fringe separation Δx is decreased if slit separation a is increased.
- The fringe separation Δx is increased as wavelength of light λ is increased.
- The weave characteristics of light cause the light to pass through the slits and interfere with each other, producing the light and dark areas on the wall behind the slits. The light that appears on the wall behind the slits is partially absorbed by the wall, a characteristic of a particle.
- Constructive interference occurs when waves interfere with each other crest-to-crest and the waves are exactly in phase with each other. Destructive interference occurs when waves interfere with each other crest-to-trough (peak-to-valley) and are exactly out of phase with each other.
- Each point on the wall has a different distance to each slit; a different number of wavelengths fit in those two paths. If the two path lengths differ by a half a wavelength, the waves will interfere destructively. If the path length differs by a whole wavelength the waves interfere constructively.
- Constructive interference – Occurs when waves interfere with each other crest to crest and the waves are exactly in phase with each other.
- Destructive interference – Occurs when waves interfere with each other crest to trough (peak to valley) and are exactly out of phase with each other.
Problem (JEE Advanced):
In Young’s double slit experiment, the intensities at two points P1 and P2 on the screen are respectively I1 and I2. If P1 is located at the centre of a bright fringe and P2 is located at a distance equal to a quarter of fringe width from P1, then find I1/I2.
Solution:
Here, y = ω = λD/4d
?x = yd/D = λ/4
φ = (2π/λ)?x = π/2
φ/2 = π/4
Now, I2 = I1 cos2(φ/2)
Or, I1/ I2 = 1/cos2(φ/2) = 2
From the above observation we conclude that, the ratio of I1/I2 would be 2.
Problem:
A beam of light consisting of two wavelengths 6500 oA and 5200 oA is used to obtain interference fringes. The distance between the slits is 2.0 mm and the distance between the plane of the slits and the screen is 120 cm.
(a) Find the distance of the third bright fringe on the screen from the central maxima for the wavelength 6500 oA.
(b) What is the least distance from the central maxima where the bright fringes due to both the wavelengths coincide?
Solution:
(i) y3 = n. Dλ/d = 3 x 1.2m x 6500 x 10-10m / 2 x 10-3m = 0.12cm
Let nth maxima of light with wavelength 6500 Å coincides with that of mth maxima of 5200Å.
(ii) m x 6500Ao x D/d = n x 5200Ao x D/d ⇒ m/n = 5200/6500 = 4/5
Least distance = y4 = 4.D (6500Ao)/d = 4 x 6500 x 10-10 x 1.2/ 2 x 10-3m = 0.16cm
Test Your knowledge
Question 1-: In Young’s experiment be performed with two slits in water instead of in air:
(a) The fringes will be smaller in number
(b) The fringes will be broader
(c) The fringes will be narrower
(d) No fringes will be obtained
Answer:- (a) The fringes will be smaller in number
QUESTION 2-: In Young’s interference experiment with one source and two slits, one slit is covered with a cello phone sheet so that half the intensity is absorbed. Then:
(a) No fringe is obtained
(b) Bright fringe will be brighter and dark fringe is darker
(c) All fringes will be darker
(d) Bright fringes will be less bright and dark fringes will be less dark.
Answer:- (c) ALL FRINGES WILL BE DARKER
QUESTION 3-: In Young’s interference experiment, the separation between the slits is halved and the distance between slits and the screen is doubled. The fringe width is:
(a) Unchanged (b) Halved
(c) Doubled (d) QuadrupleAnswer:- (d) Quadruple
QUESTION 4-: In Young’s experiment for interference of light with two slits, reinforcement takes place when sin θ = mλ/d, d is,
(a) distance from slit to screen
(b) distance between dark and bright fringe
(c) distance between the slits
(d) width of mth fringe.
Answer:- (c) distance between the slits
QUESTION 5-: In Young’s double slit experiment, the distance between the slits is gradually increased. The width of the fringes system:
(a) increases (b) decreases
(c) remains the same (d) halved
Answer:- (a) increases
|
98 videos|387 docs|104 tests
|
FAQs on Double Slit Experiment - Physics Class 12 - NEET
| 1. What is the Double Slit Experiment? |  |
| 2. How does the Double Slit Experiment support the wave-particle duality theory? |  |
| 3. What happens if the Double Slit Experiment is conducted with only one slit open? |  |
| 4. Can the Double Slit Experiment be performed with other particles besides light? |  |
| 5. What are the practical applications of the Double Slit Experiment? |  |

|
Explore Courses for NEET exam
|

|

















