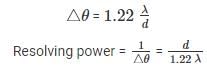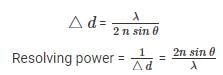Diffraction Limit
When a point object is imaged using a circular opening (or aperture) like a lens or the iris of our eye, the image formed is not a point but a diffraction pattern. This is true particularly when the size of the object is comparable to the wavelength of light.
Just as in single slit diffraction, a circular aperture produces a diffraction pattern of concentric rings that grow fainter as we move away from the center. These are known as Airy’s discs.

Because of this point sources close to one another can overlap and produce a blurred image. The half angle θ subtended by the first minimum at the source is given by the relation
sinθ ≈ 1.22 λ/d
To obtain a good image, point sources must be resolved i.e., the point sources must be imaged such that their images are sufficiently far apart that their diffraction patterns do not overlap. For this the minimum distance between images must be such that the central maximum of the first image lies on the first minimum of the second and vice versa. Such an image is said to be just resolved. This is the famous Rayleigh criterion.
The criterion is given by the above formula as:
sin θR ≈ θR≈ 1.22 λ\d



The first image is fully resolved, the second just resolved and third unresolved.
Resolving Power:
It is defined as the inverse of the distance or angular separation between two objects which can be just resolved when viewed through the optical instrument.
Resolving Power of Telescope:
In telescopes, very close objects such as binary stars or individual stars of galaxies subtend very small angles on the telescope. To resolve them we need very large apertures. We can use the Rayleigh’s to determine the resolving power. The angular separation between two objects must be

Thus higher the diameter d, better the resolution. The best astronomical optical telescopes have mirror diameters as large as 10m to achieve the best resolution. Also larger wavelengths reduce the resolving power and consequently radio and microwave telescopes need larger mirrors.
Resolving Power of Microscope:
For microscopes, the resolving power is the inverse of the distance between two objects that can be just resolved. This is given by the famous Abbe’s criterion given by Ernst Abbe in 1873 as

Where n is the refractive index of the medium separating object and aperture. Note that to achieve high resolution n sin θ must be large. This is known as the Numerical aperture.
Thus, for good resolution:
- Sin θ must be large. To achieve this, the objective lens is kept as close to the specimen as possible.
- A higher refractive index (n) medium must be used. Oil immersion microscopes use oil to increase the refractive index. Typically for use in biology studies this is limited to 1.6 to match the refractive index of glass slides used. (This limits reflection from slides). Thus the numerical aperture is limited to just 1.4-1.6. Thus, optical microscopes (if you do the math) can only image to about 0.1 micron. This means that usually organelles, viruses and proteins cannot be imaged.
- Decreasing the wavelength by using X-rays and gamma rays. While these techniques are used to study inorganic crystals, biological samples are usually damaged by x-rays and hence are not used.
The limit set by Abbe’s criterion for optical microscopy cannot be avoided. However, using different fluorescence microscopy techniques the Abbe’s limit can be circumvented. Stefan Hell used a technique called Simulated Emission Depletion (STED) and the duo Eric Betzig and W.E. Moerner used super imposed images using green fluorescent proteins to bypass the resolution limit and obtain optical images in never before seen resolution. All three were awarded the 2014 Nobel Prize in Chemistry for their pioneering work.