Euclid’s Division Algorithm | Advance Learner Course: Mathematics (Maths) Class 9 PDF Download
Euclid’s Division Algorithm is a technique to compute the Highest Common Factor (HCF) of two given positive integers. HCF of two positive integers a and b is the largest positive integer d that divides both a and b. To understand Euclid’s Division Algorithm we first need to understand Euclid’s Division Lemma.
Euclid’s Division Lemma
Euclid’s Division Lemma gives the relation between all the components of Division.
According to Euclid’s Division Lemma, for any 2 positive integers a & b there exists a unique integers q & r such that, a = b x (q + r), where 0 ≤ r < b
Let’s understand Euclid’s Division Lemma visually.
In the below diagram, the Dividend 27 is a and the Divisor 8 is b. 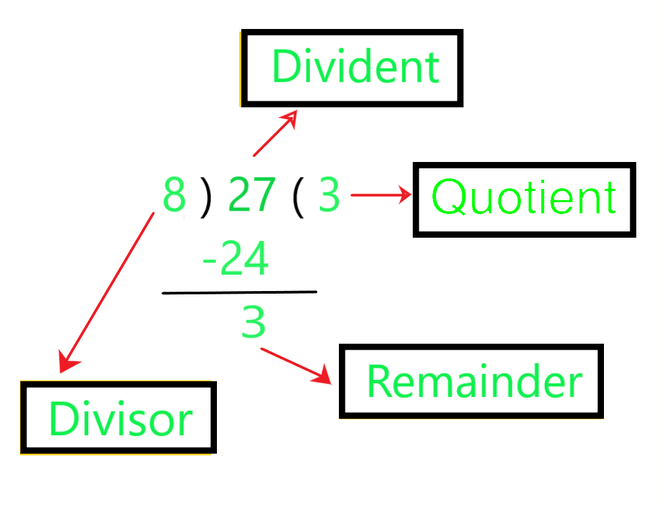 The Quotient 3 is q and the Remainder 3 is r
The Quotient 3 is q and the Remainder 3 is r 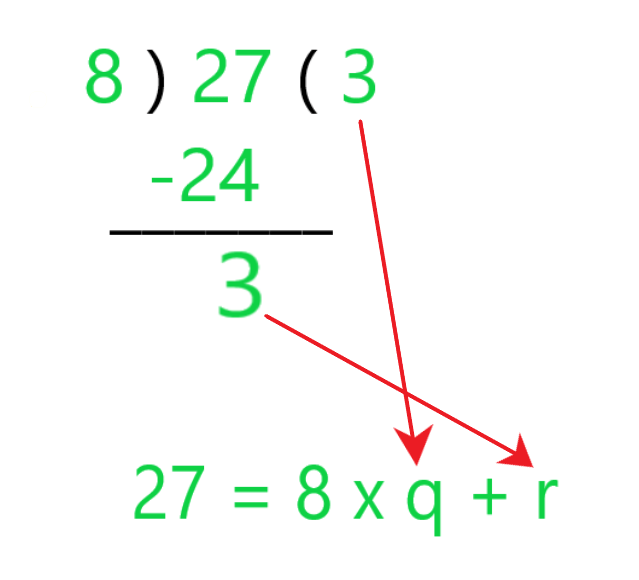 As you can see in the below image:
As you can see in the below image:
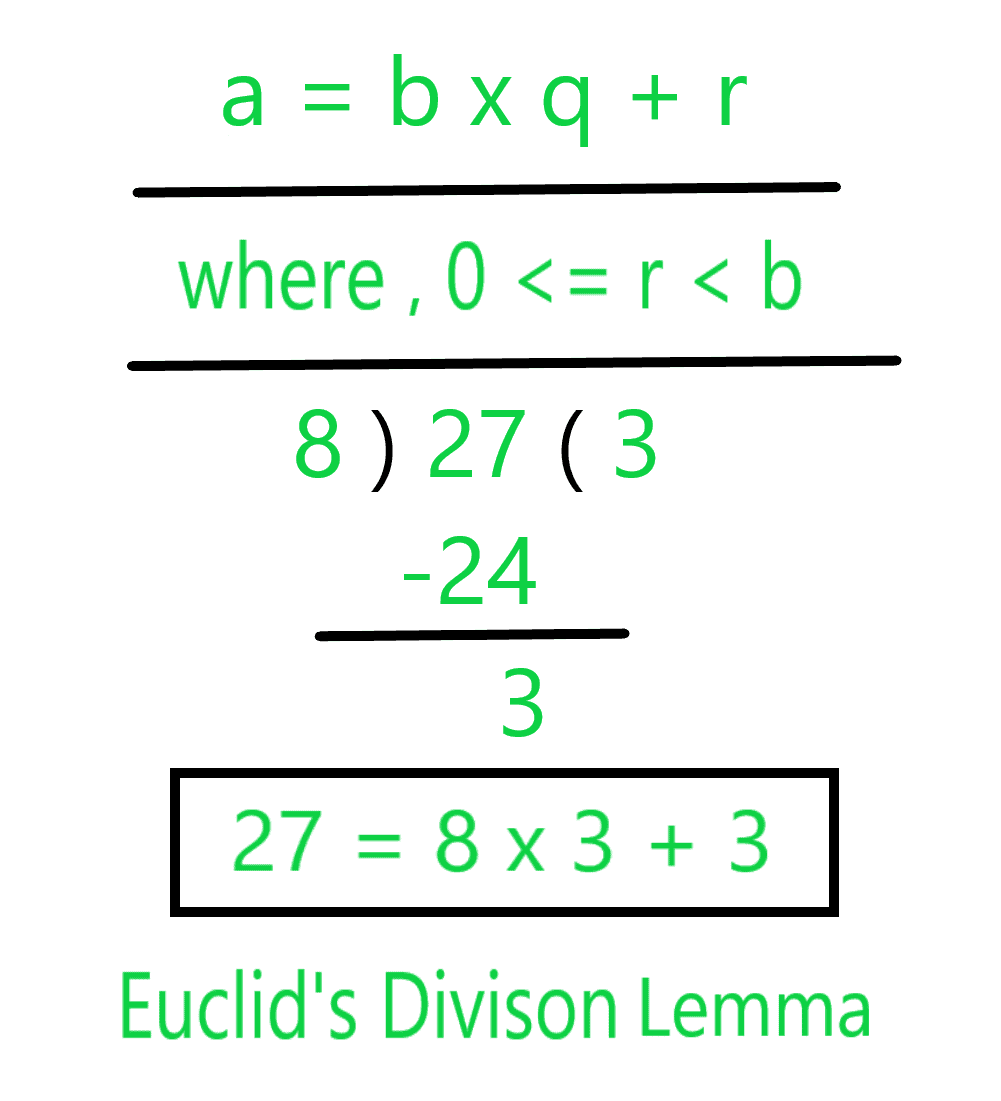
Thus, the division lemma can be written as: Dividend = (Divisor x Quotient) + Remainder
Euclid’s Division Lemma has many Applications
- It can be usen to find of Divisibility of Integers
- It can be used to find the HCF of two numbers (HCF Stands For Highest Common Factor).
Using Division Lemma to Find the HCF of Two Numbers
The process of finding the HCF of two numbers using EUCLID’S DIVISION LEMMA is called “EUCLID’S DIVISION ALGORITHM”.
Example 1: Let’s find the HCF of 135 and 255?
Solution:
Step 1: Apply the Division Lemma to the 255 and 135, by dividing 255 by 135.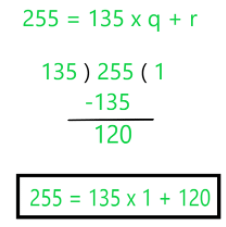
Step 2: Now, the Remainder becomes the divisor and the previous divisor becomes the dividend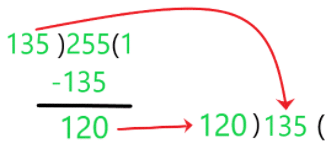
Step 3: Again Division Lemma is Applied to this new pair of Dividend and Divisor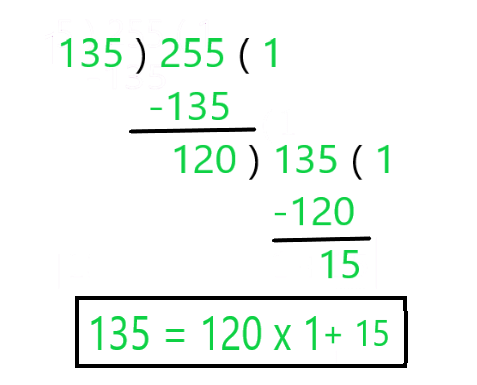
Step 4: Now 15 is our new Divisor and 120 is the new Dividend.
The Divisor which makes the Remainder Zero is the HCF of Two Numbers.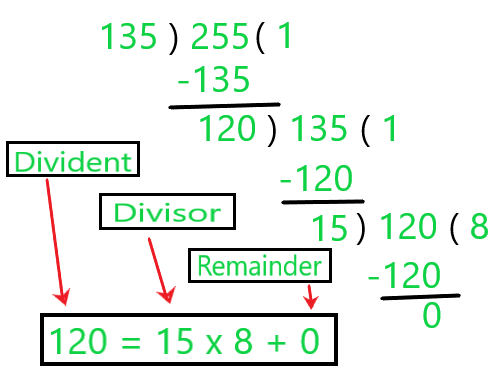
So 15 is the HCF of 255 and 135. 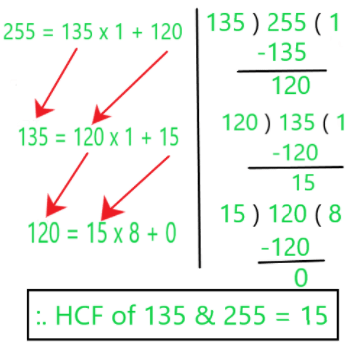
Example 2: Use Euclid’s Division Algorithm to Find the HCF of 867 and 255?
Solution:
Step 1: Since 867 > 255, we apply the Division Lemma to 867 and 255, to get
867 = 255 x 3 + 102
Step 2: Since the Remainder 102 ≠ 0, we apply the division lemma to 867 and 255, to get
255 = 102 x 2 + 51
Step 3: We consider the new divisor 102 and the new Remainder 51 and apply the division lemma to get 102 = 51 x 2 + 0
The remainder has now become zero, so our procedure stops. Since the divisor at this stage is 51, the HCF of 255 and 867 is 51.
Example 3: Use Euclid’s Division Algorithm to Find the HCF of 4052 and 12576?
Solution:
Step 1: Since 12576 > 4052 , we apply the Division Lemma to 867 and 255, to get
12576 = 4052 x 3 + 420
Step 2: Since the Remainder 420 ≠ 0, we apply the division lemma to 12576 and 4052, to get
4052 = 420 x 9 + 272
Step 3: We consider the new divisor 420 and the new Remainder 272 and apply the division lemma to get
420 = 272 x 1 + 148
We consider the new divisor 272 and the new Remainder 148 and apply the division lemma to get
272 = 148 x 1 +124
We consider the new divisor 148 and the new Remainder 124 and apply the division lemma to get
148 = 124 x 1 + 24
We consider the new divisor 124 and the new Remainder 24 and apply the division lemma to get
124 = 24 x 5 + 4
We consider the new divisor 24 and the new Remainder 4 and apply the division lemma to get
24 = 4 x 6 + 0
The remainder has now become zero, so our procedure stops . Since the divisor at this stage is 4, the HCF of 4052 and 12576 is 4.
|
13 videos|79 docs|29 tests
|
FAQs on Euclid’s Division Algorithm - Advance Learner Course: Mathematics (Maths) Class 9
| 1. What is Euclid's Division Lemma? |  |
| 2. What is Euclid's Division Algorithm? |  |
| 3. How does Euclid's Division Algorithm work? |  |
| 4. Can Euclid's Division Algorithm be used to find the least common multiple (LCM) of two numbers? |  |
| 5. Is Euclid's Division Algorithm applicable for negative numbers? |  |
|
13 videos|79 docs|29 tests
|



















