Geometry: Solved Examples- 1 | CSAT Preparation - UPSC PDF Download
Q1: O is a point in the interior of ΔABC such that OA = 12 cm, OC = 9 cm, ∠AOB = ∠BOC = ∠COA and ∠ABC = 60°. What is the length (in cm) of OB?
(a) 6√2
(b) 4√6
(c) 6√3
(d) 4√3
Ans: (c)
Given:
O is a point in the interior of ΔABC
OA = 12 cm
OC = 9 cm
∠AOB = ∠BOC = ∠COA
∠ABC = 60°
Concept used:
An angle around a point will always make a 360°
The sum of all the angles of a triangle is 180°
Calculation: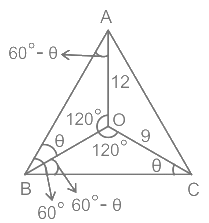
According to the question
We know that an angle around a point will always make a 360°
So,
⇒ ∠AOB = ∠BOC = ∠COA = 360/3
⇒ 120°
Now,
∠ABC = 60°
We know that the sum of all the angles of triangle is 180°
In ΔAOB
Let ∠OBA = θ
⇒ ∠OBA + ∠BAO + ∠AOB = 180°
⇒ θ + ∠BAO + 120° = 180°
⇒ ∠BAO = (180° – 120° – θ)
⇒ ∠BAO = 60° – θ
Now,
In ΔBOC
⇒ ∠OBC = (∠ABC – ∠OBA)
∠OBC = 60° – θ
⇒ ∠OBC + ∠BOC + ∠OCB = 180°
⇒ (60° – θ + 120° + ∠OCB = 180°
⇒ ∠OCB = (180° – 120° – 60° – θ)
⇒ ∠OCB = θ
So,
∠AOB and ∠BOC
⇒ ∠A = ∠B
⇒ ∠O = ∠O
⇒ ∠B = ∠C
ΔAOB ~ ΔBOC [AAA similarity]
Now,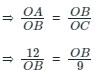
⇒ OB2 = 108
⇒ OB = 6√3 cm
∴ The required value of OB is 6√3 cm
Q2: O is the centre of the circle. A tangent is drawn which touches the circle at C. If ∠AOC = 80°, then what is the value (in degrees) of ∠BCX?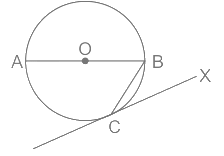
(a) 80
(b) 30
(c) 40
(d) 50
Ans: (d)
Given:
∠AOC = 80°
Concept used:
The angle subtended by the chord at center is twice the angle subtended by it at any point on the circle
Calculation: AC is a chord to the circle
AC is a chord to the circle
⇒ ∠ABC = 1/2 × ∠AOC
= 1/2 × 80
= 40°
In triangle OBC
⇒ OB = OC = radius of the circle
⇒ ∠OBC = ∠OCB = 40°
⇒ ∠XCO = 90°
Tangent is perpendicular to the radius
⇒ ∠BCX = ∠XCO – ∠OCB = 90 – 40 = 50°
∴ The value of ∠BCX is 50°
Q3: In ΔPQR, ∠Q = 85° and ∠R = 65°. Points S and T are on the sides PQ and PR, respectively such that ∠STR = 95° and the ratio of the QR and ST is 9 : 5. If PQ = 21.6 cm, then the length of PT is:
(a) 12 cm
(b) 10.5 cm
(c) 9 cm
(d) 9.6 cm
Ans: (a)
Given:
QR : ST = 9 : 5, PQ = 21.6 cm,
∠Q = 85°, ∠R = 65 and ∠STR = 95°
Concept Used:
Two triangles are similar if the measure of two angles is the same and vice-versa.
Calculation: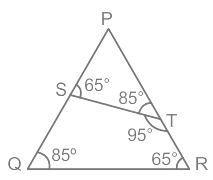
From the following figure
ΔPTS ∼ PQR
⇒ QR/TS = PQ/PT
⇒ 9/5 = 21.6/PT
⇒ PT = (21.6 × 5)/9
⇒ PT = 12 cm
∴ The length of PT is 12 cm.
Q4: Chords AB and CD of a circle, when produced, meet at a point P outside the circle, If AB = 6 cm, CD = 3 cm and PD = 5 cm, then PB is equal to∶
(a) 6 cm
(b) 4 cm
(c) 5 cm
(d) 6.25 cm
Ans: (b)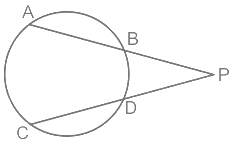
Given, AB = 6 cm, CD = 3 cm, PD = 5 cm
Let the length of PB be x, PA = (x + 6) and PC = 5 + 3 = 8 cm
As we know,
PB × PA = PD × PC
⇒ x × (x + 6) = 5 × 8
⇒ x2 + 6x – 40 = 0
⇒ x2 + 10x – 4x – 40 = 0
⇒ x (x + 10) – 4 (x + 10) = 0
⇒ (x + 10) (x – 4) = 0
⇒ (x + 10) = 0
⇒ x = -10 [not possible]
⇒ (x – 4) = 0
⇒ x = 4
Q5: In the given figure, B and C are the centres of the two circles. ADE is the common tangent to the two circles. If the ratio of the radius of both the circles is 3 : 5 and AC = 40, then what is the value of DE?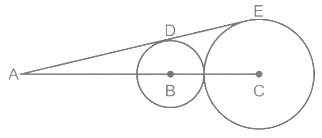 (a) 3√15
(a) 3√15
(b) 5√15
(c) 6√15
(d) 4√15
Ans: (d)
Concept Used:
Tangents are always ⊥ with the radius.
Calculation: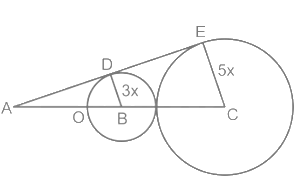 Since the ratio of the radius of both the circles is 3 : 5, let DB = 3x and EC = 5x;
Since the ratio of the radius of both the circles is 3 : 5, let DB = 3x and EC = 5x;
Since ΔABD and ΔACE are similar, AB : AC = 3 : 5;
∴ AB : BC = 3 : 2
∵ AC = 40
∴ BC = 2/5 × 40 = 16
⇒ BC = 3x + 5x = 16
⇒ x = 2
∴ BD = 3x = 6 and EC = 5x = 10.
ΔAEC is the right angle triangle;
AE2 = AC2 – EC2
AE2 = 1600 – 100 = 1500
AE = 10√15
Since AD : DE = 3 : 2
∴ DE = 2/5 × 10√15 = 4√15
Q6: If D and E are points on the sides AB and AC respectively of a triangle ABC such that DE||BC. If AD = x cm, DB = (x - 3) cm, AE = (x + 3) cm and EC = (x - 2) cm, then what is the value (in cm) of x?
(a) 3
(b) 3.5
(c) 4
(d) 4.5
Ans: (d)
The given triangle is shown below,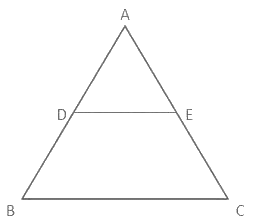 Considering similar triangles ∆ABC and ∆ADE,
Considering similar triangles ∆ABC and ∆ADE,
⇒ AB/AD = AC/AE
⇒ (AD + DB)/AD = (AE + EC)/AE
⇒ (x + x - 3)/x = (x + 3 + x - 2)/(x + 3)
⇒ (2x - 3)/x = (2x + 1)/(x + 3)
⇒ (2x - 3)(x + 3) = x(2x + 1)
⇒ 2x2 + 6x - 3x - 9 = 2x2 + x
⇒ 2x = 9
∴ x = 9/2 = 4.5
Q7: Circumcentre of ΔABC is O. If ∠BAC = 75° and ∠BCA = 80°, then what is the value (in degrees) of ∠OAC?
(a) 45
(b) 65
(c) 90
(d) 95
Ans: (b)
Given:
In ΔABC,
⇒ ∠BAC + ∠BCA + ∠ABC = 180°
⇒ ∠ABC = 180° – 75° - 80°
⇒ ∠ABC = 25°
Since O is the circumcentre
⇒ 2 × ∠ABC = ∠AOC
⇒ ∠AOC = 50°
In ΔAOC, AO = OC (radius of circle)
Hence, ΔAOC is an isosceles Δ
⇒ ∠OAC + ∠ACO + ∠AOC = 180°
⇒ ∠OAC + ∠ACO = 180° – 50°
⇒ 2 × ∠OAC = 130°
⇒ ∠OAC = 65°
∴ the correct option is 2)
Q8: In the given figure, ABC is a triangle. The bisectors of internal DB and external DC interest at D. If ∠BDC = 48°, then what is the value (in degrees) of ∠A?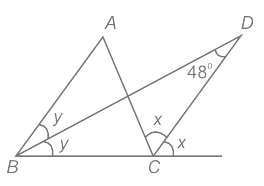 (a) 48
(a) 48
(b) 96
(c) 100
(d) 114
Ans: (b)
Given:
The bisectors of internal DB and external DC intersect at D.
∠BDC = 48°
Calculation: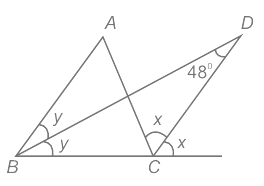
Using Exterior angle property in ΔBDC
⇒ y + 48 = x
⇒ x - y = 48° ......(i)
From ΔABC,
⇒ ∠ACB = 180 – 2y – ∠A ......(ii)
From ΔBCD,
⇒ ∠ACB = 180 – y – x – 48 ......(iii)
Comparing (ii) and (iii)
⇒ 180 – 2y – ∠A = 180 – y – x – 48
⇒ ∠A = x – y + 48
Using (i)
⇒ ∠A = 48 + 48 = 96°
∴ The value (in degrees) of ∠A is 96°.
Q9: Points P, Q, R, S and T lie in this order on a circle with centre O. If chord TS is parallel to diameter PR and ∠RQT= 58°, then find the measure (in degrees) of ∠RTS.
(a) 45
(b) 29
(c) 32
(d) 58
Ans: (c)
Given:
Points P, Q, R, S and T lie in this order on a circle with centre O
chord TS is parallel to diameter PR
∠RQT = 58°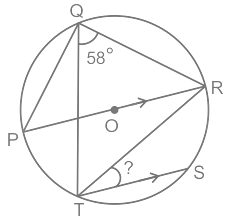 Calculation:
Calculation:
PR is a diameter
∠PTR = 90° .....(angle inscribe in a semicircle)
also ∠TPR = 58° .....(angle formed on same chord)
so, ∠PRT = 180° - ∠PTR – ∠TPR
⇒ ∠PRT = 180° - 90° - 58°
⇒ ∠PRT = 32°
∠PRT = ∠RTS = 32° (Alternate interior angle as chord TS is parallel to diameter PR)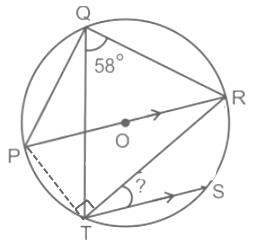 ∴ The measure of ∠RTS is 32.
∴ The measure of ∠RTS is 32.
Q10: In the given figure, a circle inscribed in ∆PQR touches its sides PQ, QR and RP at points S, T and U, respectively. If PQ = 15 cm, QR = 10 cm, and RP = 12 cm, then find the lengths of PS, QT and RU? (a) PS = 6.5 cm, QT = 8.5 cm and RU = 3.5 cm
(a) PS = 6.5 cm, QT = 8.5 cm and RU = 3.5 cm
(b) PS = 3.5 cm, QT = 6.5 cm and RU = 8.5 cm
(c) PS = 8.5 cm, QT = 6.5 cm and RU = 3.5 cm
(d) PS = 8.5 cm, QT = 3.5 cm and RU = 6.5 cm
Ans: (c)
Let PS be x cm, then QS = (15 – x) cm
PS = PU, QS = QT, RT = RU [tangents]
⇒ QT = (15 – x) cm
⇒ RT = 10 – (15 – x) = x – 5
⇒ RU = (x – 5)
⇒ PU = 12 – x + 5 = 17 – x
⇒ 17 – x = x
⇒ 2x = 17
⇒ x = 17/2
⇒ x = 8.5 cm
⇒ PS = 8.5
⇒ QT = 15 – 8.5 = 6.5
⇒ RU = 8.5 – 5 = 3.5
Q11: ΔABC, BE ⊥ AC, CD ⊥ AB and BE and CD intersect each other at O. The bisectors of ∠OBC and ∠OCB meet At P. If ∠BPC = 148°, then what is the measure of ∠A?
(a) 28°
(b) 32°
(c) 64°
(d) 56°
Ans: (c)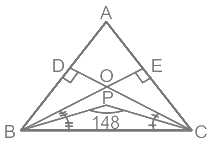 As we know,
As we know,
∠BPC = 90° + ∠BOC/2
⇒ 148° = 90° + ∠BOC/2
⇒ ∠BOC/2 = 148° – 90° = 58°
⇒ ∠BOC = 58° × 2 = 116°
⇒ ∠BOC = ∠DOE = 116° [opposite angle]
In quadrilateral ADOE
∠DAE + ∠ADO + ∠DOE + ∠OEA = 360
⇒ ∠DAE + 90° + 116° + 90° = 360°
⇒ ∠DAE = 360° – 296° = 64°
Q12: ABCD is a cyclic quadrilateral whose diagonals intersect at P. If AB = BC, ∠DBC = 70° and ∠BAC = 30°, then the measure of ∠PCD is:
(a) 50°
(b) 35°
(c) 55°
(d) 30°
Ans: (a)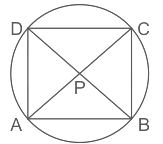
In ΔABC,
If AB = BC
then ∠BAC = ∠BCA = 30°
⇒ ∠BAC + ∠BCA + ∠ABC = 180°
⇒ ∠ABC = 180° – 30° – 30° = 120°
⇒ ∠ABC = ∠ABD + ∠DBC
⇒ 120° = ∠ABD + ∠DBC
⇒ ∠ABD = 50°
As we know,
⇒ ∠ABD = ∠ACD = 50° (angles drawn from the same base to the circumference of circle)
and we can write ∠ACD = ∠PCD
or ∠PCD = 50°
Q13: An equilateral triangle of area 300 cm2 is cut from its three vertices to form a regular hexagon. Area of hexagon is what percent of the area of triangle?(Each side of the regular hexagon is 1/3 rd the original side of equilateral triangle)
(a) 66.66%
(b) 33.33%
(c) 83.33%
(d) 56.41%
Ans: (a)
Each side of the regular hexagon is 1/3 rd the original side of equilateral triangle
⇒ Area of regular hexagon = (3√3/2) × (side)2
⇒ (3√3/2) × (side of triangle/3)2
⇒ (√3/6) × side of triangle2
⇒ (2/3) × (√3/4) × side of triangle2
⇒ 2/3 × Area of equilateral triangle = (2/3) × 100 = 66.66%
∴ Required percentage is 66.66%
Q14: ΔXYZ is similar to ΔPQR. If ratio of Perimeter of ΔXYZ and Perimeter of ΔPQR is 4 : 9 and if PQ = 27 cm, then what is the length of XY (in cm)?
(a) 9
(b) 12
(c) 16
(d) 15
Ans: (b)
Given that ΔXYZ is similar to ΔPQR
Since they are similar we know,
(Perimeter of ∆XYZ)/(perimeter of ∆PQR) = (length of XY)/(length of PQ)
Ratio of Perimeter of ΔXYZ and Perimeter of ΔPQR is 4 : 9
⇒ 4/9 = (length of XY)/27
⇒ Length of XY = 4/9 × 27= 12 cm
∴ Length of XY is 12 cm
Q15: In the given figure, triangle ABC is drawn such that AB is tangent to a circle at A whose radius is 10cm and BC passes through centre of the circle. Point C lies on the circle. If BC = 36cm and AB = 24cm, then what is the area (in cm2) of triangle ABC?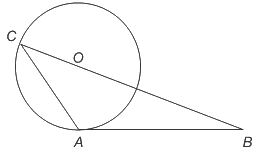 (a) 134.5
(a) 134.5
(b) 148
(c) 166.15
(d) 180
Ans: (c)
Join OA where OA = 10 cm
Here, AO is perpendicular to AB
⇒ Area of ∆ABC = Area of ∆OAB + Area of ∆AOC
⇒ Area of ∆ABC = 1/2(OA)(AB) + 1/2(OC)(OA)sin(∠AOC)
⇒ Area of ∆ABC = 1/2(10)(24) + 1/2(10)(10) sin(∠AOC)
⇒ Area of ∆ABC = 120 + 50 sin(∠AOC)
In right angled ∆OAB
⇒ tan(∠AOB) = 24/10 = 12/5
⇒ ∠AOB = 67.38°
So, ∠AOC = 180° – 67.38° = 112.62°
Hence, Area of ∆ABC = 120 + 50 (0.93) = 120 + 46.15 = 166.15
∴ The area (in cm2) of triangle ABC is 166.15.
|
207 videos|249 docs|138 tests
|
FAQs on Geometry: Solved Examples- 1 - CSAT Preparation - UPSC
| 1. What are the basic concepts of geometry? |  |
| 2. How is geometry used in real life? |  |
| 3. What are the different types of angles in geometry? |  |
| 4. How can geometry help in problem-solving? |  |
| 5. What are the different types of polygons in geometry? |  |

















