Mensuration: Volume, Surface Area & Solid Figures - CSAT Preparation - UPSC PDF Download

What is Mensuration?

Mensuration is the branch of mathematics concerned with measuring geometric quantities: lengths, areas and volumes. It covers 2-dimensional figures (where we measure length and area) and 3-dimensional solids (where we measure surface areas - curved, lateral and total - and volume). Mensuration gives formulae and methods to compute these quantities from given dimensions (lengths, radii, heights, slant heights, etc.).

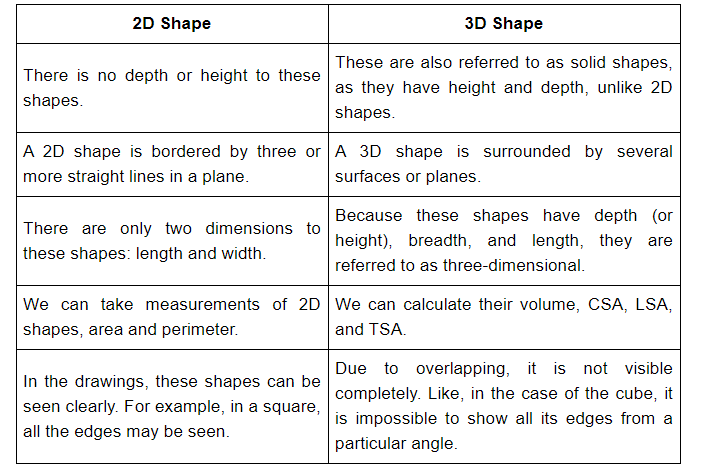
2D and 3D Shapes

Mensuration distinguishes between flat (plane) figures and solid (three-dimensional) figures. Plane figures include triangles, quadrilaterals, polygons and circles. Solid figures include prisms, cylinders, cones, pyramids, spheres and combinations of these.

Important Terms in Mensuration

• Area (A): The surface covered by a closed 2D shape, measured in square units.
• Perimeter (P): The total length of the boundary of a 2D shape, measured in linear units.
• Volume (V): The amount of space enclosed by a 3D object, measured in cubic units.
• Curved Surface Area (CSA): Area of the curved portion of a solid, excluding its base(s) and any flat faces.
• Lateral Surface Area (LSA): Sum of the areas of the vertical (or lateral) faces; for solids without curved faces, this excludes top and bottom faces.
• Total Surface Area (TSA): Sum of the areas of all outer faces of a closed solid.
• Square Unit: Area of a square with sides of one unit (e.g., m², cm²).
• Cubic Unit: Volume of a cube with sides of one unit (e.g., m³, cm³).

Tools Used for Mensuration

• Caliper: for accurate measurement of small diameters and thicknesses.
• Try square: to check squareness and straight edges in constructions.
• Meter stick / Tape: for measuring linear distances and lengths.
• Compass: to draw circles and arcs.
• Protractor: to measure and construct angles.

Key Formulas for Common Solids

SOLID	Total Surface Area	Lateral / Curved Surface Area	Volume	Leading Diagonal / Slant Height
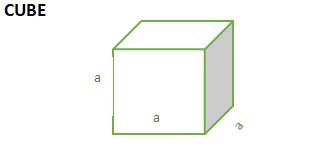	6a²	4a²	a³	√3 a
	2(LB + BH + HL)	2H (L + B)	LBH	√(L² + H² + B²)
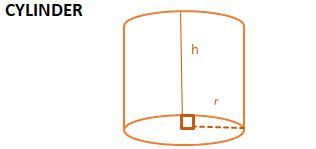	2πr (r + h)	2πrh	πr²h	No slant height / diagonal
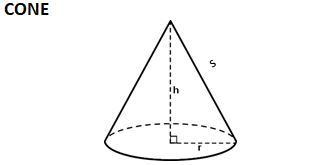	πr (r + l)	πrl	⅓ π r² h	√(h² + r²)
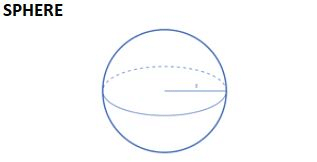	4πr²	4πr²	4/3 π r³	No slant height / diagonal
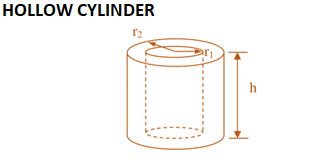	2π(r1 + r2) (r2 - r1 + h)	2πh(r1 + r2)	πh(r2² - r1²)	No slant height / diagonal
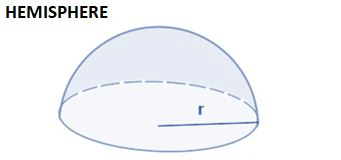	3πr²	2πr²	2/3 π r³	No slant height / diagonal

Prism

A prism is a solid with two congruent, parallel polygonal bases and parallelogram side faces. The cross-section parallel to the base is identical along the prism's length.

• Overview: The number of side faces equals the number of sides of the polygonal base.
• Base and Side Faces: The number of side faces on a prism corresponds to the number of sides in the polygonal base. For instance, if the base is triangular, the prism will have three side faces. Similarly, if the base is a quadrilateral, the prism will have four side faces, and so on.
• Right prism: side edges are perpendicular to the base; examples include cuboids (rectangular prism) and right triangular prisms.

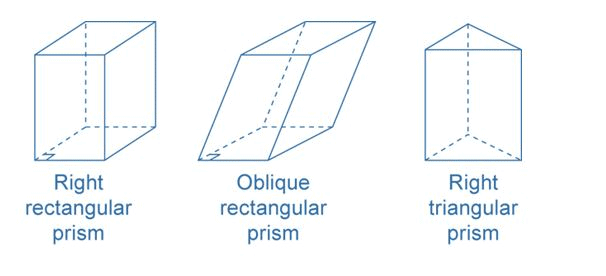
Mensuration of Prism

• Lateral Surface Area (LSA): LSA = (perimeter of base) × (height of prism).
• Total Surface Area (TSA): TSA = LSA + 2 × (area of base).
• Volume (V): V = (area of base) × (height).

Pyramids

A pyramid has a polygonal base and triangular faces that meet at a single apex. A right pyramid has the apex directly above the centroid of the base.

• A pyramid with an n-sided base has n + 1 vertices, n + 1 faces and 2n edges.
• Common example: a square-based right pyramid (like the Egyptian pyramids) has four triangular faces and one square base.

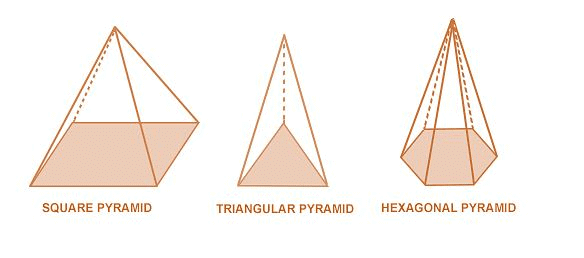
Mensuration of Pyramid

• Lateral surface area of a pyramid = (perimeter of base × slant height) / 2.
• Total surface area = lateral surface area + area of base.
• Volume = (1/3) × (area of base) × (vertical height).

Quadrilateral

To find the area of a general quadrilateral, one convenient method is to split it into two triangles along a diagonal and sum the areas of the triangles.

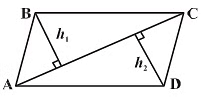
• Area of ABCD = Area of ∆ABC + Area of ∆ACD
  = (1/2) × AC × h₁ + (1/2) × AC × h₂

Thus, Area of Quadrilateral = (1/2) × d × (h1 + h2), where d is the common diagonal AC and h1, h2 are corresponding heights from the diagonal.

Rhombus

A rhombus is a quadrilateral with all sides equal. Its diagonals bisect each other at right angles.

Area of a rhombus = (1/2) × (product of diagonals) = ½ × d1 × d2.

Mensuration of Quadrilaterals

Use decomposition into triangles, trapezia or use formulae specific to rectangles, squares, rhombi, kites and trapeziums as applicable.

Circles

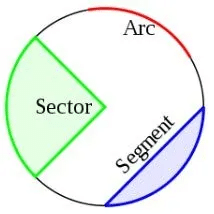
• Circumference of the circle = 2πr
• Area of the circle = πr²
• Length of arc = 
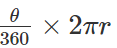
• Area of Sector = 
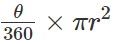
• Area of Segment = 

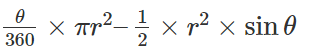
Triangles

• Formula of Perimeter of triangle (P) = a + b + c

  

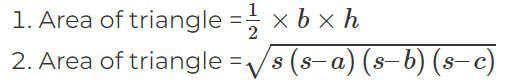
• Some advanced mensuration formulas for area of triangle are:
  

Polygons

Cuboid, Cube and Cylinder

• Surface Area: Use the net of the solid and add areas of faces; unit is square unit.
• Lateral / Curved Surface Area: Area excluding top and bottom faces; unit is square unit.

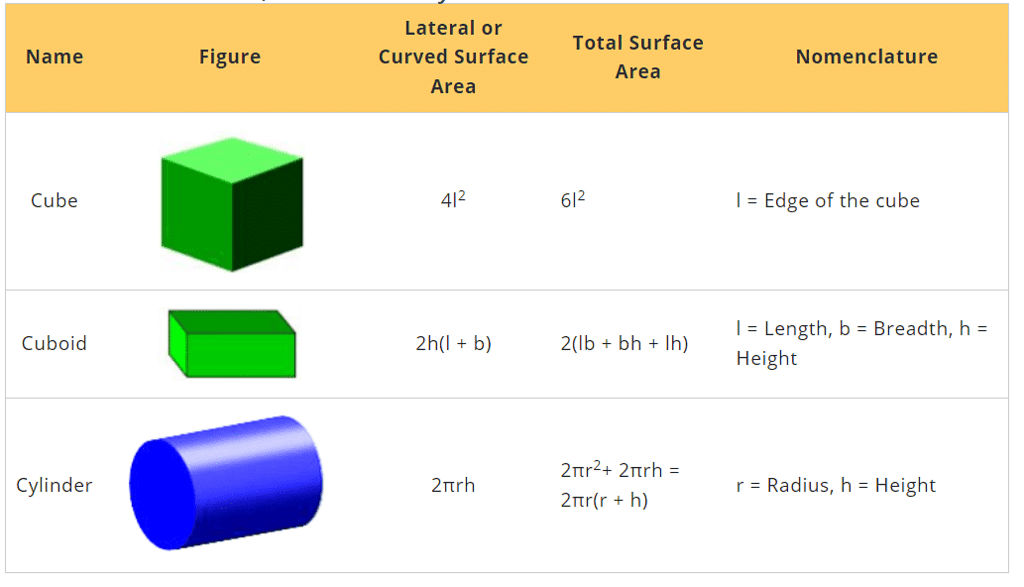
• Volume: Space occupied by the solid; units are cubic units.

Cone

• Curved Surface Area = π r l, where l is slant height.
• Total Surface Area = π r (r + l).
• Volume = (1/3) π r² h.

Sphere

• Total Surface Area = 4 π r².
• Volume = (4/3) π r³.

Hemisphere

• Curved Surface Area = 2 π r².
• Total Surface Area = 3 π r² (includes base circle).
• Volume = (2/3) π r³.

Practice Questions

Problem 1: The length of a garden is thrice its breadth. A playground measuring 180 sq. m occupies 1/15th of the total area of the garden. The length of the garden is

1. 60 m
2. 30 m
3. 90 m
4. 50 m

Sol: Correct Answer is Option 3

Let L be the length and B be the breadth of the garden.

L = 3B.

Total area of the garden = 180 × 15 = 2700 sq m.

Therefore, L × B = 2700.

Substitute L = 3B to get 3B² = 2700.

B² = 900.

B = 30 m.

Hence, L = 3 × 30 = 90 m.

Problem 2:  The perimeter of an equilateral triangle is 96√3 cm. Find its height.

1. 32 cm
2. 48 cm
3. 16 cm
4. 64 cm
5. 24 cm

Sol: Correct Answer is Option 2

Perimeter = 96√3 cm.

Each side = (96√3) / 3 = 32√3 cm.

Height of an equilateral triangle = (√3 / 2) × side.

Height = (√3 / 2) × 32√3 = (√3 × 32√3) / 2.

= (32 × 3) / 2.

= 48 cm.

Problem 3: If the ratio of radius of two spheres is 4:7, the ratio of their volume is

1. 4 : 7
2. 64 : 343
3. 49 : 16
4. 16 : 49
5. None of these

Sol: Correct Answer is  Option 2

Ratio of radii = 4 : 7.

Volume scales as the cube of the radius.

Therefore, volume ratio = 4³ : 7³ = 64 : 343.

Problem 4: The diameter (in metre) of a sphere whose volume is 268 (4/21) m³ is

1. 6
2. 12
3. 8
4. 24
5. 16

Sol: Correct Answer is Option 3

Given volume = 268 (4/21) m³ = 5632 / 21 m³.

Volume of a sphere = (4/3) π r³.

(4/3) π r³ = 5632 / 21.

Solve for r³: r³ = (5632 / 21) × (3 / 4) × (1 / π).

Using π = 22/7 gives r³ = (5632 / 21) × (3 / 4) × (7 / 22).

Compute simplified value to get r³ = 64.

Therefore r = 4 m.

Diameter = 2r = 8 m.

Problem 5:  The slant height of a right circular cone is 13 m and its height is 5 m. Find the area of the curved surface.

1. 490.28 m²
2. 288.28 m²
3. 450 m²
4. 200 m²
5. None of these

Sol: Correct Answer is Option 1

Curved surface area of a cone = π r l.

Given slant height l = 13 m and vertical height h = 5 m.

Use Pythagoras: r = √(l² - h²).

r = √(13² - 5²).

= √(169 - 25).

= √144 = 12 m.

Curved area = π × 12 × 13.

Using π = 22/7 gives area = (22/7) × 12 × 13 = 490.2857... ≈ 490.28 m².

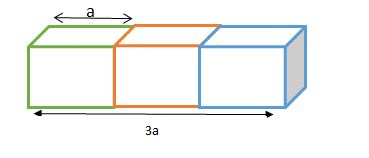
Problem 6: If three cubes are placed adjacently in a row, then the ratio of the total surface area of the new cuboid to the sum of the surface area of the three cubes will be

1. 1:3
2. 2:3
3. 5:9
4. 7:9

Correct Answer is Option (4)

Let each cube have side a.

When placed in a row, the resulting cuboid has dimensions 3a × a × a.

TSA of cuboid = 2(3a×a + a×a + 3a×a).

= 2(3a² + a² + 3a²).

= 2 × 7a² = 14a².

TSA of three separate cubes = 3 × 6a² = 18a².

Required ratio = 14a² : 18a² = 7 : 9.

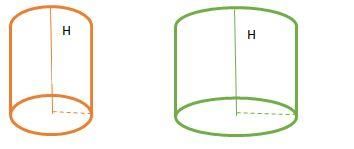
Problem 7: X and Y are two cylinders of the same height. The base of X has diameter that is half the diameter of the base of Y. If the height of X is doubled, the volume of X becomes
(1) Equal to the volume of Y
(2) Double the volume of Y
(3) Half the volume of Y
(4) Greater than the volume of Y

Correct Answer is Option (3)

Original solids:

Let radius of X be r and radius of Y be 2r (since diameter of X is half that of Y).

Volume of X initially = π r² H.

Volume of Y = π (2r)² H = 4 π r² H.

If height of X is doubled, new volume of X = π r² × 2H = 2 π r² H.

Compare with Y: 2 π r² H = (1/2) × 4 π r² H.

Therefore the new volume of X is half the volume of Y.

Problem 8: Water is poured into an empty cylindrical tank at a constant rate for 5 minutes. After the water has been poured into the tank, the depth of the water is 7 feet. The radius of the tank is 100 feet. Which of the following is the best approximation for the rate at which the water was poured into the tank

1. 140 cubic feet/sec
2. 440 cubic feet/sec
3. 733 cubic feet/sec
4. 2200 cubic feet/sec

Correct Answer is Option (3)

Volume of water in tank = π r² h.

= (22/7) × 100² × 7.

= (22/7) × 10,000 × 7.

= 22 × 10,000 = 220,000 ft³.

Time = 5 minutes = 300 seconds.

Rate = 220,000 / 300 = 733.333... ft³/sec.

Approximation = 733 ft³/sec.

Problem 9: A conical cavity is drilled in a circular cylinder of 15 cm height and 16 cm base diameter. The height and base diameter of the cone is the same as those of the cylinder. Determine the total surface area of the remaining solid?
(1) 215 Π cm²
(2) 376 Π cm²
(3) 440 Π cm²
(4) 542 Π cm²

Correct Answer is Option (3)

In this question, we are given a cylinder out of which a cone is removed and we need to find out the total surface area of the remaining solid given in the above figure.
Therefore, T.S.A of the remaining solid = C.S.A of cylinder + C.S.A of the cone + area of the base of cylinder
= 2Πrh + Πrl + Πr²
= Π(2 × 8 × 15 + 8 × 17 + 8²)
= Π(240 + 136 + 64)
= 440Π cm²

Problem 10: Base of a right prism is a rectangle; the ratio of whole length and breadth is 3:2. If the height of the prism is 12 cm and total surface area is 288 cm², then the volume of the prism is

1. 291 cm³
2. 288 cm³
3. 290 cm³
4. 286 cm³

Correct Answer is Option (2)

Since the prism has a rectangular base, the prism formed is a cuboid with the ratio of length and breadth as 3:2 and height is 12 cm. Therefore T.S.A of cuboid = 288 cm²
288 = 2(lb + bh + hl)
288 = 2(3x × 2x + 2x × 12 + 12 × 3x)
288 = 2(6x² + 24x + 36x)
144 = 6x² + 60x
x² + 10x – 24 = 0
x² + 12x – 2x – 24 = 0
(x + 12)(x – 2) = 0
x = 2
Therefore, length is 6 cm and breadth is 4 cm. Thus, volume of cuboid = l × b × h = 6 × 4 × 12 = 288 cm³

Problem 11: Five marbles of various sizes are placed in a conical funnel. Each marble is in contact with the adjacent marble(s). Also, each marble is in contact all around the funnel wall. The smallest marble has a radius of 8 mm. The largest marble has a radius of 18 mm. What is the radius (in mm) of the middle marble?

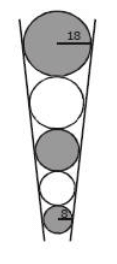1. 10
2. 11
3. 12
4. 15

Correct Answer is Option (3)

The marbles touch each other and the funnel wall in a manner that their radii form a geometric progression between 8 mm and 18 mm across five marbles.

General formula for geometric progression: r_n = r_1 × q^(n-1).

Here r_1 = 8, r_5 = 18 and n = 5.

So 18 = 8 × q^4.

q^4 = 18/8 = 9/4 = (3/2)².

Hence q^2 = 3/2 ⇒ q = √(3/2).

Middle marble is the 3rd term: r_3 = 8 × q² = 8 × (3/2) = 12 mm.

Problem 12: Three identical cones with base radius r are placed on their base so that each is touching the other two. The radius of the circle drawn through their vertices is 

1. Smaller than r
2. Equal to r
3. Larger than r
4. Depends on the height of the cones

Correct Answer is Option (3)

When three identical cones of base radius r are placed with their bases on the same plane and each base touching the other two, the centres of bases form an equilateral triangle of side 2r.

The circumradius R of an equilateral triangle of side s is R = s / √3.

With s = 2r, the circumradius = (2r) / √3 = (2/√3) r, which is greater than r (since 2/√3 ≈ 1.155 > 1).

Therefore the radius of the circle through the vertices is larger than r.