Square Roots and Cube Roots | Quantitative Aptitude (Quant) - CAT PDF Download
Square Roots and Cube Roots
To find the square root of a number, you want to find some number that when multiplied by itself gives you the original number. In other words, to find the square root of 25, you want to find the number that when multiplied by itself gives you 25. The square root of 25, then, is 5. The symbol for square root is √0. Following is a list of the first eleven perfect (whole number) square roots.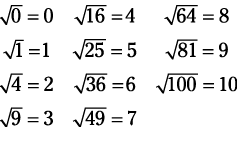
Special note: If no sign (or a positive sign) is placed in front of the square root, then the positive answer is required. Only if a negative sign is in front of the square root is the negative answer required. This notation is used in many texts and is adhered to in this book. Therefore,

Cube roots
To find the cube root of a number, you want to find some number that when multiplied by itself twice gives you the original number. In other words, to find the cube root of 8, you want to find the number that when multiplied by itself twice gives you 8. The cube root of 8, then, is 2, because 2 × 2 × 2 = 8. Notice that the symbol for cube root is the radical sign with a small three (called the index) above and to the left 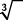 . Other roots are defined similarly and identified by the index given. (In square root, an index of two is understood and usually not written.) Following is a list of the first eleven perfect (whole number) cube roots.
. Other roots are defined similarly and identified by the index given. (In square root, an index of two is understood and usually not written.) Following is a list of the first eleven perfect (whole number) cube roots.
Approximating square roots
To find the square root of a number that is not a perfect square, it will be necessary to find an approximate answer by using the procedure given in Example.
Example 1
Approximate √42.
Since 62 = 36 and 72 = 49, then √42 is between √36 and √49.
Therefore, √42 is a value between 6 and 7. Since 42 is about halfway between 36 and 49, you can expect that √42 will be close to halfway between 6 and 7, or about 6.5. To check this estimation, 6.5 × 6.5 = 42.25, or about 42.
Square roots of nonperfect squares can be approximated, looked up in tables, or found by using a calculator. You may want to keep these two in mind:
Simplifying square roots
Sometimes you will have to simplify square roots, or write them in simplest form. In fractions, 2/4 can be reduced to 1/2. In square roots, √32 can be simplified to  .
.
There are two main methods to simplify a square root.
Method 1: Factor the number under the 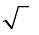 into two factors, one of which is the largest possible perfect square. (Perfect squares are 1, 4, 9, 16, 25, 36, 49, …)
into two factors, one of which is the largest possible perfect square. (Perfect squares are 1, 4, 9, 16, 25, 36, 49, …)
Method 2: Completely factor the number under the 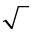 into prime factors and then simplify by bringing out any factors that came in pairs.
into prime factors and then simplify by bringing out any factors that came in pairs.
Example 2
Simplify √32.
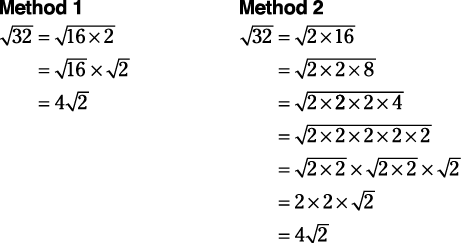
In Example , the largest perfect square is easy to see, and Method 1 probably is a faster method.
Example 3
Simplify √2016.
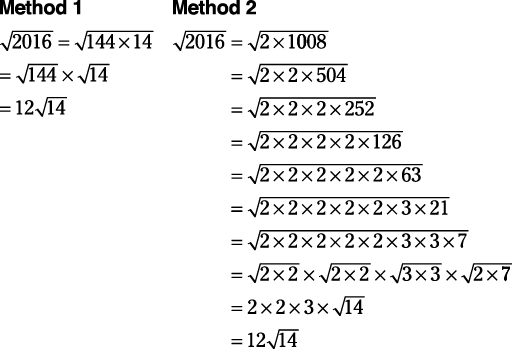
In Example , it is not so obvious that the largest perfect square is 144, so Method 2 is probably the faster method.
Many square roots cannot be simplified because they are already in simplest form, such as √7, √10, and √15.
Square, Cube, Square Root and Cubic Root for Numbers Ranging 0 - 100
| Number x | Square x2 | Cube x3 | Square Root x1/2 | Cubic Root x1/3 |
| 1 | 1 | 1 | 1 | 1 |
| 2 | 4 | 8 | 1.414 | 1.26 |
| 3 | 9 | 27 | 1.732 | 1.442 |
| 4 | 16 | 64 | 2 | 1.587 |
| 5 | 25 | 125 | 2.236 | 1.71 |
| 6 | 36 | 216 | 2.449 | 1.817 |
| 7 | 49 | 343 | 2.646 | 1.913 |
| 8 | 64 | 512 | 2.828 | 2 |
| 9 | 81 | 729 | 3 | 2.08 |
| 10 | 100 | 1000 | 3.162 | 2.154 |
| 11 | 121 | 1331 | 3.317 | 2.224 |
| 12 | 144 | 1728 | 3.464 | 2.289 |
| 13 | 169 | 2197 | 3.606 | 2.351 |
| 14 | 196 | 2744 | 3.742 | 2.41 |
| 15 | 225 | 3375 | 3.873 | 2.466 |
| 16 | 256 | 4096 | 4 | 2.52 |
| 17 | 289 | 4913 | 4.123 | 2.571 |
| 18 | 324 | 5832 | 4.243 | 2.621 |
| 19 | 361 | 6859 | 4.359 | 2.668 |
| 20 | 400 | 8000 | 4.472 | 2.714 |
| 21 | 441 | 9261 | 4.583 | 2.759 |
| 22 | 484 | 10648 | 4.69 | 2.802 |
| 23 | 529 | 12167 | 4.796 | 2.844 |
| 24 | 576 | 13824 | 4.899 | 2.884 |
| 25 | 625 | 15625 | 5 | 2.924 |
| 26 | 676 | 17576 | 5.099 | 2.962 |
| 27 | 729 | 19683 | 5.196 | 3 |
| 28 | 784 | 21952 | 5.292 | 3.037 |
| 29 | 841 | 24389 | 5.385 | 3.072 |
| 30 | 900 | 27000 | 5.477 | 3.107 |
| 31 | 961 | 29791 | 5.568 | 3.141 |
| 32 | 1024 | 32768 | 5.657 | 3.175 |
| 33 | 1089 | 35937 | 5.745 | 3.208 |
| 34 | 1156 | 39304 | 5.831 | 3.24 |
| 35 | 1225 | 42875 | 5.916 | 3.271 |
| 36 | 1296 | 46656 | 6 | 3.302 |
| 37 | 1369 | 50653 | 6.083 | 3.332 |
| 38 | 1444 | 54872 | 6.164 | 3.362 |
| 39 | 1521 | 59319 | 6.245 | 3.391 |
| 40 | 1600 | 64000 | 6.325 | 3.42 |
| 41 | 1681 | 68921 | 6.403 | 3.448 |
| 42 | 1764 | 74088 | 6.481 | 3.476 |
| 43 | 1849 | 79507 | 6.557 | 3.503 |
| 44 | 1936 | 85184 | 6.633 | 3.53 |
| 45 | 2025 | 91125 | 6.708 | 3.557 |
| 46 | 2116 | 97336 | 6.782 | 3.583 |
| 47 | 2209 | 103823 | 6.856 | 3.609 |
| 48 | 2304 | 110592 | 6.928 | 3.634 |
| 49 | 2401 | 117649 | 7 | 3.659 |
| 50 | 2500 | 125000 | 7.071 | 3.684 |
| 51 | 2601 | 132651 | 7.141 | 3.708 |
| 52 | 2704 | 140608 | 7.211 | 3.733 |
| 53 | 2809 | 148877 | 7.28 | 3.756 |
| 54 | 2916 | 157464 | 7.348 | 3.78 |
| 55 | 3025 | 166375 | 7.416 | 3.803 |
| 56 | 3136 | 175616 | 7.483 | 3.826 |
| 57 | 3249 | 185193 | 7.55 | 3.849 |
| 58 | 3364 | 195112 | 7.616 | 3.871 |
| 59 | 3481 | 205379 | 7.681 | 3.893 |
| 60 | 3600 | 216000 | 7.746 | 3.915 |
| 61 | 3721 | 226981 | 7.81 | 3.936 |
| 62 | 3844 | 238328 | 7.874 | 3.958 |
| 63 | 3969 | 250047 | 7.937 | 3.979 |
| 64 | 4096 | 262144 | 8 | 4 |
| 65 | 4225 | 274625 | 8.062 | 4.021 |
| 66 | 4356 | 287496 | 8.124 | 4.041 |
| 67 | 4489 | 300763 | 8.185 | 4.062 |
| 68 | 4624 | 314432 | 8.246 | 4.082 |
| 69 | 4761 | 328509 | 8.307 | 4.102 |
| 70 | 4900 | 343000 | 8.367 | 4.121 |
| 71 | 5041 | 357911 | 8.426 | 4.141 |
| 72 | 5184 | 373248 | 8.485 | 4.16 |
| 73 | 5329 | 389017 | 8.544 | 4.179 |
| 74 | 5476 | 405224 | 8.602 | 4.198 |
| 75 | 5625 | 421875 | 8.66 | 4.217 |
| 76 | 5776 | 438976 | 8.718 | 4.236 |
| 77 | 5929 | 456533 | 8.775 | 4.254 |
| 78 | 6084 | 474552 | 8.832 | 4.273 |
| 79 | 6241 | 493039 | 8.888 | 4.291 |
| 80 | 6400 | 512000 | 8.944 | 4.309 |
| 81 | 6561 | 531441 | 9 | 4.327 |
| 82 | 6724 | 551368 | 9.055 | 4.344 |
| 83 | 6889 | 571787 | 9.11 | 4.362 |
| 84 | 7056 | 592704 | 9.165 | 4.38 |
| 85 | 7225 | 614125 | 9.22 | 4.397 |
| 86 | 7396 | 636056 | 9.274 | 4.414 |
| 87 | 7569 | 658503 | 9.327 | 4.431 |
| 88 | 7744 | 681472 | 9.381 | 4.448 |
| 89 | 7921 | 704969 | 9.434 | 4.465 |
| 90 | 8100 | 729000 | 9.487 | 4.481 |
| 91 | 8281 | 753571 | 9.539 | 4.498 |
| 92 | 8464 | 778688 | 9.592 | 4.514 |
| 93 | 8649 | 804357 | 9.644 | 4.531 |
| 94 | 8836 | 830584 | 9.695 | 4.547 |
| 95 | 9025 | 857375 | 9.747 | 4.563 |
| 96 | 9216 | 884736 | 9.798 | 4.579 |
| 97 | 9409 | 912673 | 9.849 | 4.595 |
| 98 | 9604 | 941192 | 9.899 | 4.61 |
| 99 | 9801 | 970299 | 9.95 | 4.626 |
| 100 | 10000 | 1000000 | 10 | 4.642 |
|
167 videos|229 docs|95 tests
|
FAQs on Square Roots and Cube Roots - Quantitative Aptitude (Quant) - CAT
| 1. What are square roots and cube roots? |  |
| 2. How can I find the square root of a number? |  |
| 3. How can I find the cube root of a number? |  |
| 4. Are square roots and cube roots always positive? |  |
| 5. Can I find the square root or cube root of a negative number? |  |






















