Introduction to the Principle of Mathematical Induction | Mathematics for Airmen Group X - Airforce X Y / Indian Navy SSR PDF Download
Introduction to Mathematical Induction
Mathematical thinking is essential, as it helps in better understanding of problems thus letting us reach to solutions in a better way. Deductive reasoning and mathematical thinking are connected, as the former forms the basis of the latter. Deductive reasoning further is based on logic and understanding. See the example given underneath:
a. The German shepherd is a dog.
b. All dogs have an immaculate sense of hearing.
c. The German shepherd has an immaculate sense of hearing.
Now, if statements a) and b) are true then c) is also true. This theory of reasoning can be used mathematically as well, let’s see how?
a. Sixteen is divisible by Two.
b. Any number divisible by two is an even number.
c. Sixteen is an even number.
From the above example, we get a hint of deduction.
The deduction is the statement that needs to be proven and is generally called a theorem in mathematics. With the help of deductive steps, we prove or disprove theorems also called as conjectures that let us establish mathematical facts and principles. In a nutshell, the deduction is the application of general cases to a particular case.
Inductive reasoning is the opposite of deductive reasoning. Inductive reasoning depends on the study of a particular case and observing incidences leading to that case. This implies that in inductive reasoning we observe each and every case that lets us reach conclusions for a particular case.
Reasoning through induction forms the basis of scientific reasoning and if generally used in mathematics. Since collecting and analyzing information is a norm in scientific reasoning, mathematical induction also uses the same norms to generalize particular facts or cases.
The principle of mathematical induction is used in algebra or other streams of mathematics that involve the formulation of results or statements in terms of “n”. To prove the basic principle behind ‘n’, which is a positive integer, we use a set of well-established and well-suited principles in a specific format. The techniques used to prove statements with regard to “n” are known as principles of mathematical induction.
The Principle of Mathematical Induction
As a mathematical technique of proving things, mathematical induction is essentially used to prove the property of natural numbers (n). According to the principle of mathematical induction, a property X(n) holds to be same for all natural numbers, 0,1,2,3…… n. Let’s consider a given statement X(n) involving natural number n, so that
a. The statement is true for n = 1 i.e., X(1) is true, and
b. If the statement is true for n=k, where k is a positive integer, then the statement is also true for all cases of n= k+1 i.e., X(k) leads to the truth of X(k+1).
This means that X(n) is true for all the natural numbers, n.
Property a) mentioned above is simply a statement of a fact. In situations, where the statement is also true for all the cases of n≥5, then the step a) shall start from n=5 and we shall hence verify the result for n=5, i.e., X(5).
Property b) is a conditional property as it does not confirm that the given statement is true for n=k, but if it is true for n=k then it shall also be true for n=k+1.
Therefore to prove a property we need to first prove the conditional proposition. Proving a conditional proposition is referred to as inductive step of a theorem. The presumption that the given statement, is true, in this case, n=k is termed as the inductive hypothesis.
Example
Mathematics follows a pattern, one of the many patterns is given below
1 = 12 = 1
4 = 22= 1 + 3
9 = 32 = 1 + 3 + 5
16 = 42 = 1 + 3 + 5 + 7
25 = 52 = 1 + 3 + 5 + 7 + 9
From the above pattern example, we come to a conclusion that the square of the second natural number is equal to the sum of first two odd natural numbers. Likewise, the sum of first three odd natural numbers is equal to the square of the third natural number. From the above pattern we conclude that,
1 + 3 + 5 + 7 + … + (2n – 1) = n2 , or the square of n is equal to the sum of first n odd natural numbers. Now let us write this as,
X(n) = 1 + 3 + 5 + 7 + 9 +…….+ (2n-1) = n2
With the help of the principle of mathematical induction, we need to prove that X(n) is true for all the values of n. The first step in this process is to prove the value X(1) is true. This first step is called the base step or basic step, as it forms the basis of mathematical induction. 1 = 12 , X(1) therefore is true.
The next step following the base is called the inductive step. In this step we suppose that X(m) is true for any positive integer m, we also need to prove that X(m+1) is true. Since X(m) is true we have,
1 + 3 + 5 + 7…. + (2m-1) = m2 (1)
Now consider, 1 + 3 + 5 + 7 +….+ (2m-1) + {2(m+1)-1} (2)
Using (1), we get
= m2 + (2m + 1) = (m + 1)2
Therefore, X(m + 1) is also true thus completing our inductive proof step. This gives us that X(n) is true for all the natural numbers. Through the above example, we have proved that X(n) is true for all natural numbers n.
Solved Example For You
Question: Prove that m≥ 1 prove that, 12+ 22 + 32 +42 +……+ m2 = m(m + 1)(2m + 1)/6
Solution: Let the given statement be X(m), i.e.,
X(m) = 12+ 22 + 32 +42 +……+m2 = m(m + 1) (2m + 1) / 6
for m= 1 , X(1) = 1(1 + 1) (2 × 1 + 1) /6
= 1 × 2 × 3 / 6 = 1, which is true.
Now, lets take a positive integer, p, and assume X(p) to be true i.e.,
12+ 22 + 32 +42 +……+p2 = p(p+1) (2p+1) / 6 (1)
We shall now prove that X(p+1) is also true, so now we have,
12+ 22 + 32 +42 +……+p2 + (p+1)2
= p(p+1)(2p+1) / 6 + (p+1)2
= p(p+1)(2p+1)+6(p+1)2 / 6
= (p+1) {( 2p2 + p) + 6(p+1)} /6
= (p+1) (2p2 +7p+6)/6
= (p+1) (p+1+1) {2(p+1) +1 /6
Thus X(p + 1) is true, whenever X(p) is true for all natural numbers.
Principle of Mathematical Induction Examples
Question 1 :By the principle of mathematical induction, prove that, for n ≥ 1
1.2 + 2.3 + 3.4 + · · · + n.(n + 1) = n(n + 1)(n + 2)/3
Solution :
Let p(n) = 1.2 + 2.3 + 3.4 + · · · + n.(n + 1) = n(n + 1)(n + 2)/3
Step 1 :
put n = 1
p(1) = 1.2 + 2.3 + 3.4 + · · · + 1.(1 + 1) = 1(1 + 1)(1 + 2)/3
1 = 1
Hence p(1) is true.
Step 2 :
Let us assume that the statement is true for n = k
p(k) = 1.2 + 2.3 + · · · + k.(k + 1) = k(k + 1)(k + 2)/3 ----(1)
We need to show that P(k + 1) is true. Consider,
Step 3 :
Let us assume that the statement is true for n = k + 1
p(k+1)
1.2 + 2.3 + · · · k(k + 1) + (k+1).(k + 2) = (k+1)(k+2)(k+3)/3
By applying (1) in this step, we get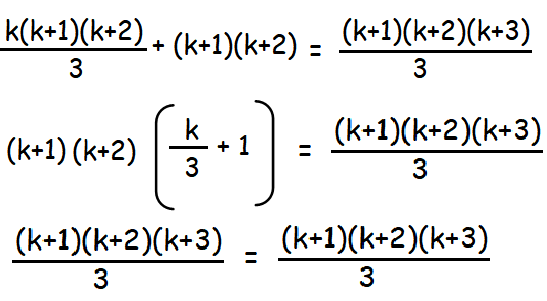
Hence, by the principle of mathematical induction for n ≥ 1
1.2 + 2.3 + 3.4 + · · · + n.(n + 1) = n(n + 1)(n + 2)/3
Question 2 : Using the Mathematical induction, show that for any natural number n ≥ 2
(1 − 1/22) (1 − 1/32)(1 − 1/42) ...............(1 − 1/n2) =(n + 1)/2n
Solution :
Let p(n) = (1 − 1/22) (1 − 1/32)(1 − 1/42) ...............(1 − 1/n2)
Step 1 :
(1 − 1/22) (1 − 1/32)(1 − 1/42) ...............(1 − 1/n2) =(n + 1)/2n
put n = 2
p(2) = (3/4) = 3/4
Hence p(2) is true.
Step 2 :
Let us assume that the statement is true for n = k
(1 − 1/22) (1 − 1/32) ..................(1 − 1/k2) =(k + 1)/2k --(1)
We need to show that P(k + 1) is true. Consider,
Step 3 :
Let us assume that the statement is true for n = k + 1
p(k+1)
(1 − 1/22) (1 − 1/32) ................(1 − 1/k2) + (1 − 1/(k+1)2)
= (k + 2)/2(k + 1)
By applying (1) in this step, we get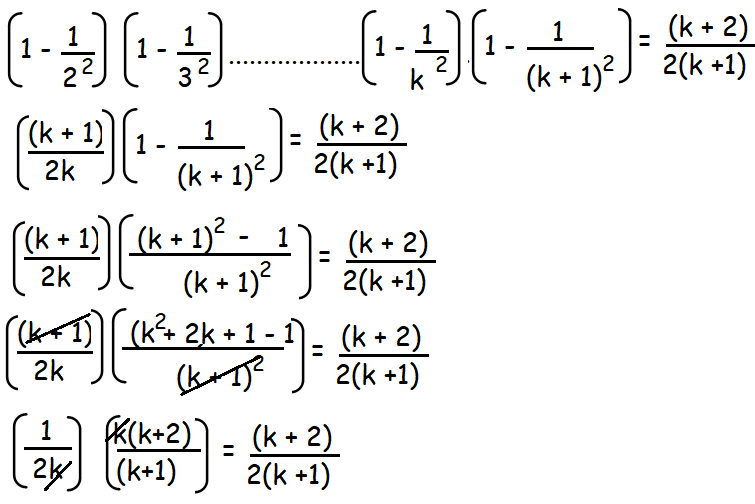
(k + 2)/2(k + 1) = (k + 2)/2(k + 1)Hence, by the principle of mathematical induction natural number n ≥ 2,
(1 − 1/22) (1 − 1/32)(1 − 1/42) ...............(1 − 1/n2) =(n + 1)/2n
|
149 videos|192 docs|197 tests
|
FAQs on Introduction to the Principle of Mathematical Induction - Mathematics for Airmen Group X - Airforce X Y / Indian Navy SSR
| 1. What is the principle of mathematical induction? |  |
| 2. How does mathematical induction work? |  |
| 3. Can you provide an example of mathematical induction? |  |
| 4. What are the key steps in applying mathematical induction? |  |
| 5. How is mathematical induction different from other proof techniques? |  |

|
Explore Courses for Airforce X Y / Indian Navy SSR exam
|

|

















