Various Forms of the Equation of Line | Mathematics (Maths) for JEE Main & Advanced PDF Download
A line is a set of all possible points lying on it. An equation of a line shows the relationship between the various points of the lines. Does this mean that any point can lie on the line? An equation of line sets the conditions for the points to satisfy. The equation of line is algebraic in nature consisting of variables x and y. By the equation of line, we can do some future estimation and can get to know about the types of lines.
Vertical Line
The equation of a vertical line at a distance v from the y-axis is either x = v or x = −v. Sign depends upon the position of the line.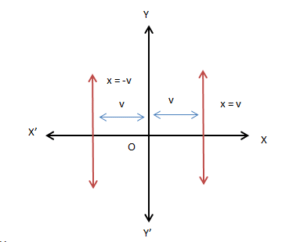
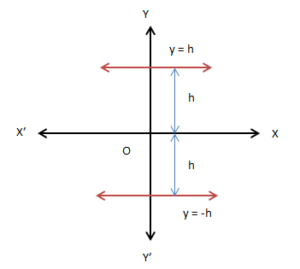
Horizontal Line
The equation of a horizontal line at a distance h from the x-axis is either y = h or y = −h. Sign depends upon the position of the line.
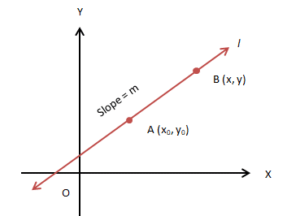
Point-Slope Form
This form of the equation gives the condition for a point to lie on the line. Suppose A (x0, y0) be a fixed point on the line l of slope m. Consider any other point, say B (x, y). The point B (x, y) will lie on the line l if and only if, its coordinates satisfy the equation
m = (y − y0) / (x − x0) (from the definition of slope)
i.e., y − y0 = m (x − x0)
What if two points are given? Let’s find out.
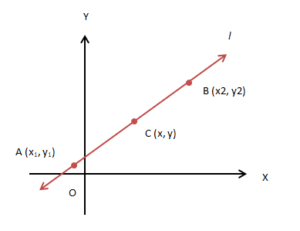
Two–Points Form
Imagine a line l passing through two points A (x1, y1) and B (x2, y2). Consider a point, say C (x, y). This point will satisfy the condition to lie on l if they satisfy the condition of collinearity.
Slope of AC = Slope of BC = Slope of AC
i.e., (y − y1) / (x − x1) = (y2 − y1) / (x2 − x1) or, (y − y1) = (x − x1) (y2 − y1) / (x2 − x1) is the required equation of the line.
Slope-Intercept Form
What is an intercept? A y-intercept is a distance at which the line intersects the y-axis. An x-intercept is a distance at which the line cuts the x-axis. Suppose a line l with slope m intersects the y-axis at a distance ‘c’ from the origin. The equation of line l passing through the point (0, c) is given by:
m = (y − c) / (x − 0) or, y = mx + c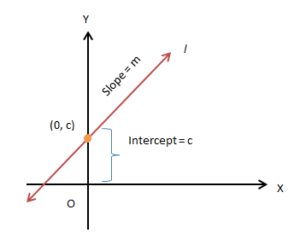
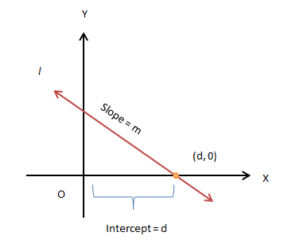
Consider a line l with slope m intersects the x-axis at a distance ‘d’ from the origin. The equation of line l passing through the point (d, 0) is given by:
m = (y − 0) / (x − d) or, y = m(x − d)
If the line l intersects both the axes what will be the equation of the line?
Intercept Form
Suppose a line l with slope m intersect the y-axis at a distance ‘c’ from the origin and x-axis at a distance of ‘d’ from the origin. The equation of line l passing through point (0, c) and (d, 0) is:
(y − y1) / (x − x1) = (y2 − y1) / (x2 − x1) or, (y − 0) / (x − d) = (c − 0) / (0 − d)
Solving we get, y/c + x/d = 1.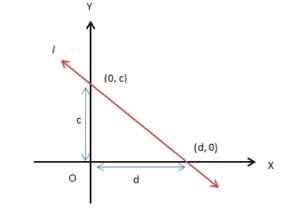
Normal Form
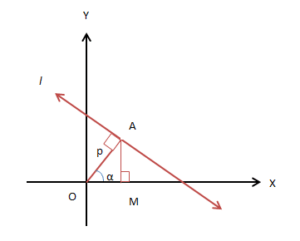
Suppose we have a line l in XY-plane. The perpendicular distance (normal) from origin to the line is known and the angle with the positive direction of the x-axis.
Here, length of normal OA = p and it makes an angle α with the x-axis. The coordinates of A will be (p cosα, p sinα). OA is perpendicular to l. Slope of line l = −1 / slope of OA = −1 / tan α. Solving we have the required equation of the line, x cos α + y sin α = p. Till now, we have seen that the equations of the line are linear equations in x and y and can be generalized.
General Equation of Line
The general equation for any line is Ax + By + C = 0, where x and y are variables; A and B are not zero simultaneously. It is interesting to know that the general equation of a line can be reduced into any form of the equations.
Slope–Intercept Form
If B ≠ 0, then Ax + By + C = 0 can be reduced to y = − (A/B) x − C/B (of the form y = mx + c). Here, the slope of the line, m = − A/B, and y-intercept, c = −C/B. If B = 0, x = −C/A is the x-intercept.
Intercept Form
If C ≠ 0, then Ax + By + C = 0 can be reduced to (x/ (− C/A)) + (y/ (− C/B)) = 1 (of the form x/a + y/b = 1). Here, x-intercept = −C/A, and y-intercept = −C/B. If C = 0, Ax + By = 0 ⇒ A = B = 0. It shows a line passing through origin.
Normal Form
The normal form of equation is x cosα + y sinα = p. Reducing it in the form of Ax + By + C = 0, we have cosα = ±A/(A2 + B2)1/2; sin α = ±B/(A2 + B2)1/2 and p = ±C /(A2+ B2)1/2.
Solved Example
Problem: Find the slope and the x and y-intercepts from the equation 4x + 5y − 8 = 0.
Solution: Given equation 4x + 5y − 8 = 0 can be re-written as y = − (4/5) x + 8/5.
Comparing with y = mx + c, we have slope,
m = − 4/5, y–intercept, c = 8/5.
Comparing with y = m(x − d), we have
y = − 4/5(x − 2). So, x-intercept = 2.
|
172 videos|503 docs|154 tests
|
FAQs on Various Forms of the Equation of Line - Mathematics (Maths) for JEE Main & Advanced
| 1. What are the different forms of the equation of a line? |  |
| 2. How can I convert a line equation from slope-intercept form to point-slope form? |  |
| 3. What is the general form of a line equation and how is it derived? |  |
| 4. How can I convert a line equation from point-slope form to slope-intercept form? |  |
| 5. Can I convert a line equation directly from general form to slope-intercept form? |  |