Scientific Notation & Significant Figures | Physics Class 11 - NEET PDF Download
| Table of contents |

|
| Introduction |

|
| Scientific Notation |

|
| What are Significant Figures? |

|
| Multiplication and Division |

|
| Order of Magnitude |

|
| Rounding |

|
Introduction
There are effective methods for managing numbers and presenting data in a clear and accurate way, such as:
- Scientific Notation: This is a way to express very large or very small numbers using powers of ten, which makes calculations easier and more manageable.
- Significant Figures: This concept helps in determining which digits in a number are meaningful and contribute to its precision, ensuring that measurements are reported accurately.
- Dimensional Analysis: This technique involves converting units from one measurement to another in a systematic way, ensuring that calculations are consistent and correct.
Scientific Notation
- Scientific Notation is a way of expressing numbers that are too big or too small to be conveniently written in decimal form.
- In which any number can be represented in form N × 10n (where n is an exponent having positive or negative values and N can vary between 1 to 10).
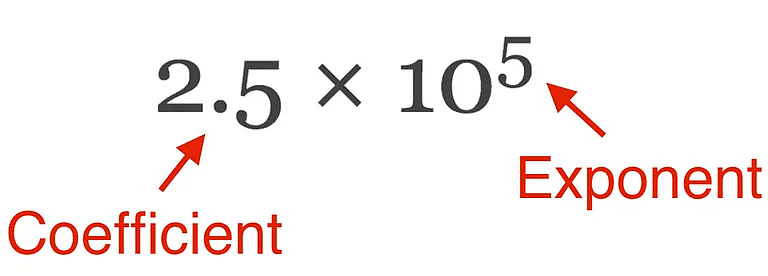 Scientific Notation
Scientific Notation
Example: We can write 232.508 as 2.32508 × 102 in scientific notation. Similarly, 0.00016 can be written as 1.6 × 10–4.
Thus, we can write 232.508 as 2.32508 × 102 in scientific notation. Note that while writing it, the decimal had to be moved to the left by two places and the same is the exponent (2) of 10 in the scientific notation.
Similarly, 0.00016 can be written as 1.6 × 10–4. Here the decimal has to be moved four places to the right and (– 4) is the exponent in the scientific notation.
Multiplication and Division for Exponential Numbers
- These two operations follow the same rules which are there for exponential numbers, i.e.
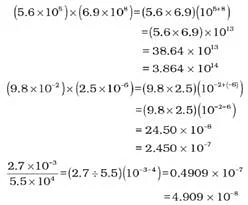
Addition and Subtraction for Exponential Numbers
- For these two operations, first, the numbers are written in such a way that they have the same exponent. After that, the coefficients (digit terms) are added or subtracted as the case may be.
- Thus, for adding 6.65 × 104 and 8.95 × 103, the exponent is made the same for both numbers. Thus, we get (6.65 × 104) + (0.895 × 104).
Examples:
Q.1. Which of the following options is not correct?
(a) 8008 = 8.008 x 103
(b) 208 = 3
(c) 5000 = 5.0 x 103
(d) 2.0034 = 4
Ans: (d)
Solution:
2.0034 = 4
Q.2. Exponential notation in which any number can be represented in the form, Nx 10n here N is termed as
(a) non –digit term
(b) digit term
(c) numeral
(d) base term
Ans: (b)
Solution:
In exponential notation N × 10n, N is a number called digit term which varies between 1.000 and 9.000….
What are Significant Figures?
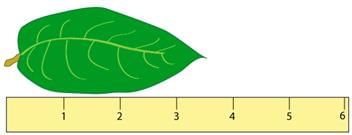
- The accuracy of a measurement depends on how it is taken. For instance, measuring the length of a leaf with a ruler that has markings every centimeter (cm) leads to different estimations compared to a ruler with millimeter (mm) markings.
- When using a cm ruler, one might estimate the leaf's length as 3.5 cm, indicating the measurement's precision.
- However, a mm ruler allows for a more precise estimation, such as 3.52 cm, showcasing the ruler's ability to capture finer details.
- The number of digits in a measurement reflects its maximum accuracy, which is why they are called significant digits or significant figures.
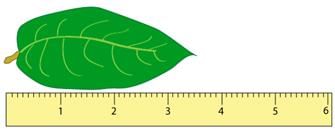
Using the second ruler, it’s possible to estimate that the leaf is 3.52 cm long, but it is not possible to measure that accurately with the first ruler. In this way, the number of digits in the measured value gives us an idea of the maximum accuracy of the measurement. These are called significant digits or significant figures.
Rules for Significant Figures
- All non-zero numbers are significant. For example, the number 33.2 has three significant figures because all the digits are non-zero.
- Zeros between two non-zero digits are significant. The number 2051 has four significant figures, as the zero is between 2 and 5.
- Leading zeros are not significant. They serve as "placeholders." For instance, 0.54 has only two significant figures. Similarly, 0.0032 also has two significant figures, as all the zeros are leading.
- Trailing zeros to the right of the decimal are significant. For example, 92.00 contains four significant figures. This indicates a measurement to the nearest hundredth of a millilitre, unlike 92, which is only accurate to the nearest millilitre. It's crucial to understand that "zero" signifies information, not just absence.
- Trailing zeros in a whole number with the decimal shown are significant. By convention, a decimal at the end indicates that the trailing zero is significant. For example, "540." shows there are three significant figures.
- Trailing zeros in a whole number with no decimal shown are not significant. Writing just "540" means the zero is not significant, giving only two significant figures.
- Exact numbers have an infinite number of significant figures. This applies to defined quantities. For example, 1 metre has infinite significant figures. For rounding 1000.3 to four significant figures, we see that 1000.3 has five significant figures. Thus, we drop the final 3, leaving us with 1000 as the four-significant-figure answer.
- For a number in scientific notation: N × 10 x , all digits in N are significant by the first six rules; "10" and "x" are not significant. For instance, 5.02 × 10 4 has three significant figures: "5.02." The "10" and "4" do not count. To express 1100 with three significant figures, we can write it as 1.10 × 10 3 , which reflects three significant figures.
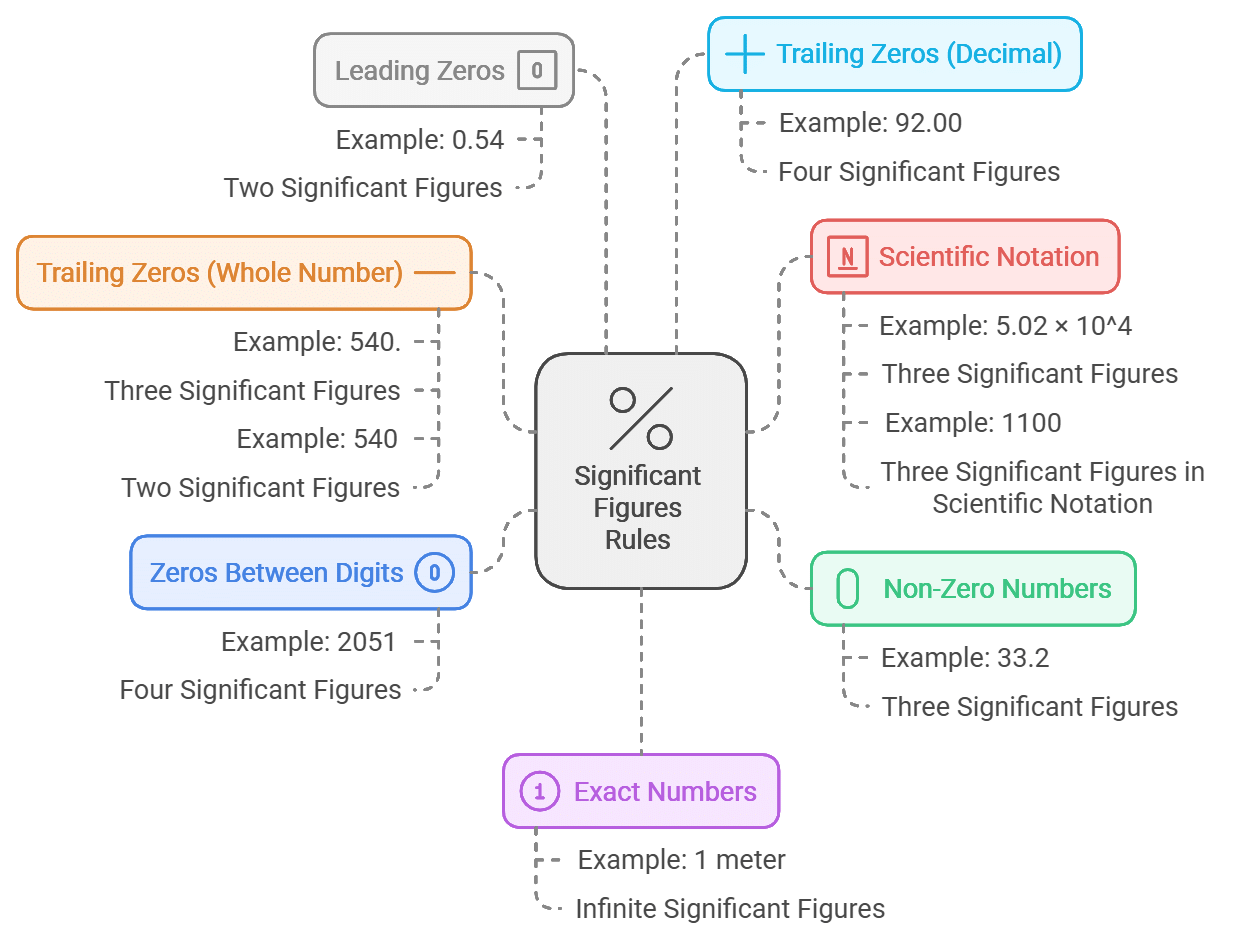
Addition and Subtraction
When it comes to calculations involving significant figures, the approach differs depending on whether you're adding, subtracting, multiplying, or dividing. Let's focus on addition and subtraction first.
Rule for Addition and Subtraction:
Limit the final answer to the rightmost column where all the numbers being added or subtracted have significant figures.
Example: Adding 1.2 and 4.71
- 1.2 has significant figures in the tenths column.
- 4.71 has significant figures in the hundredths column.
Since 1.2 is the limiting factor, we round the final answer to the tenths column.
Rounding Rule:
Round up if the first dropped digit is 5 or greater, and round down if it is less than 5.

Multiplication and Division
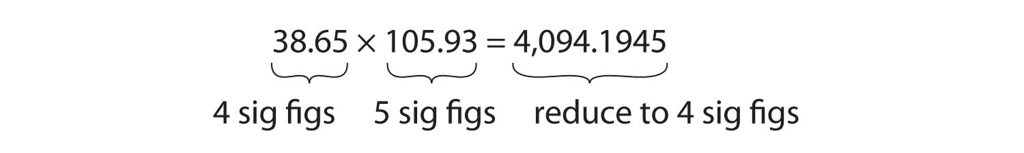
When multiplying or dividing numbers, it's important to consider the number of significant figures in each number. The final answer should have the same number of significant figures as the number with the fewest significant figures.
Example:
- If you multiply 12.11 (which has four significant figures. by 1.2 (which has two significant figures ), the result should be rounded to two significant figures because 1.2 has the fewer significant figures.
- The calculation 12.11 × 1.2 = 14.5532, but rounded to two significant figures, it becomes 15.
Example 2:
- If you multiply 12.11 (four significant figures) by 1.20 (three significant figures), the result should be rounded to three significant figures.
- The calculation 12.11 × 1.20 = 14.5532, but rounded to three significant figures, it becomes 14.6.
Scientific notation is a helpful method to express significant figures clearly:
- The number 450 has two significant figures and is written as 4.5 × 10 2 .
- In contrast, 450.0 has four significant figures and is written as 4.500 × 10 2 .
Scientific notation ensures that all significant figures are clearly represented.
Order of Magnitude
- The order of magnitude of a quantity is a way to express its size using powers of ten. To determine this, you round the value to the nearest power of ten. The rounding rule is simple: if the last digit is less than 5, you leave it as is; if it's 5 or greater, you round up.
- When you divide a number by 10 raised to its order of magnitude, the result will always be between 0.5 and 5. This means you can express the number as 0.5 < x="">< 5="">, where x is the order of magnitude.
Example: Let's look at some examples to understand the order of magnitude better:
(a) 49 can be written as 4.9 × 10 1 , so the order of magnitude is 1.
(b) 51 is 5.1 × 10 1 , which gives an order of magnitude of 2.
(c) 0.049 is 4.9 × 10 -2 , so the order is -2.
(d) 0.050 is 5.0 × 10 -2 , leading to an order of -1.
(e) 0.051 is 5.1 × 10 -2 , resulting in an order of -1 as well.
Rounding
When doing calculations using significant figures, you will find it necessary to round your answer to the nearest significant digit. There are therefore a few rules of rounding that help retain as much accuracy as possible in the final answer.
- Complete all sequential calculations BEFORE doing any rounding, since rounding early reduces the number of significant figures available for subsequent calculations.
- If the last significant digit is followed by a 6, 7, 8, or 9, round up.
Example: 5.677, rounded to three significant digits, is 5.68
- If the last significant digit is followed by a 0, 1, 2, 3, or 4, simply drop the trailing digits.
Example: 561200, rounded to three significant digits, is 561000
- If the last significant digit is EVEN, and is followed by a 5, drop the trailing digits.
Example: 45850, rounded to three significant digits, is 45800
- If the last significant digit is ODD, and is followed by a 5, round up.
Example: 3.47588, rounded to three significant digits, is 3.48
AMBIGUOUS ZEROS
So what happens if your calculation or measurement ends in a zero? For example, what if you measured a branch that was 200 cm (not 199 or 201 cm) long? The zeros in a measured value of 200 cm in this case appear ambiguous, since it could suggest that there is only one significant digit.
One way to reduce this ambiguity is to use significant figures with scientific notation.
|
96 videos|367 docs|98 tests
|
FAQs on Scientific Notation & Significant Figures - Physics Class 11 - NEET
| 1. What is scientific notation and why is it used? |  |
| 2. How do I determine the number of significant figures in a measurement? |  |
| 3. How do I apply significant figures when multiplying or dividing? |  |
| 4. What is order of magnitude and how is it calculated? |  |
| 5. How do I properly round numbers in scientific notation? |  |
















