JAMB Exam > JAMB Notes > Physics for JAMB > Relation between Electric Field, Potential & Potential Energy of a System of Charges
Relation between Electric Field, Potential & Potential Energy of a System of Charges | Physics for JAMB PDF Download
Introduction
- Electric Potential: The potential energy per unit charge at a point in a static electric field; voltage.
- Electric Field: A region of space around a charged particle, or between two voltages; it exerts a force on charged objects in its vicinity.
- For a uniform field, the relationship between electric field (E), potential difference between points A and B (Δ), and distance between points A and B (d) is: E = - Δϕ/d
- If the field is not uniform, calculus is required to solve. Potential is a property of the field that describes the action of the field upon an object.
Relation Between Electric Field and Electric Potential
- The relationship between electric potential and field is similar to that between gravitational potential and field in that the potential is a property of the field describing the action of the field upon an object.
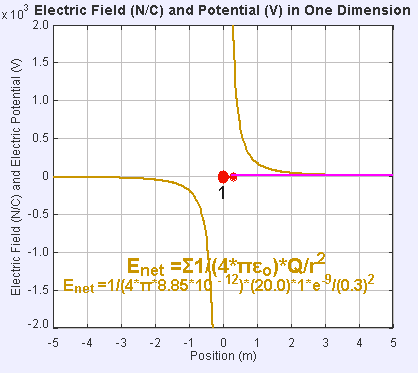 Electric Field and Potential in one Dimension
Electric Field and Potential in one Dimension - The presence of an electric field around the static point charge (large red dot) creates a potential difference, causing the test charge (small red dot) to experience a force and move.
- The electric field is like any other vector field—it exerts a force based on a stimulus, and has units of force times inverse stimulus. In the case of an electric field the stimulus is charge, and thus the units are NC-1. In other words, the electric field is a measure of force per unit charge.
- The electric potential at a point is the quotient of the potential energy of any charged particle at that location divided by the charge of that particle. Its units are JC-1. Thus, the electric potential is a measure of energy per unit charge.
- In terms of units, electric potential and charge are closely related. They share a common factor of inverse Coulombs (C-1), while force and energy only differ by a factor of distance (energy is the product of force times distance).
- Thus, for a uniform field, the relationship between electric field (E), potential difference between points A and B (Δ), and distance between points A and B (d) is:
E = - Δϕ/d - The -1 coefficient arises from repulsion of positive charges: a positive charge will be pushed away from the positively charged plate, and towards a location of higher-voltage.
- The above equation is an algebraic relationship for a uniform field. In a more pure sense, without assuming field uniformity, electric field is the gradient of the electric potential in the direction of x:
Ex = − dx/dV . - This can be derived from basic principles. Given that ∆P=W (change in the energy of a charge equals work done on that charge), an application of the law of conservation of energy, we can replace ∆P and W with other terms. ∆P can be substituted for its definition as the product of charge (q) and the differential of potential (dV). We can then replace W with its definition as the product of q, electric field (E), and the differential of distance in the x direction (dx):
qdV = −qExdx.
Potential Energy of A System of Charges
- Consider the charges q1 and q2 initially at infinity and determine the work done by an external agency to bring the charges to the given locations.
- Suppose, charge q1 is brought from infinity to the point r1. There is no external field against which work needs to be done, so work done in bringing q1 from infinity to r1 is zero. This charge produces a potential in space given by
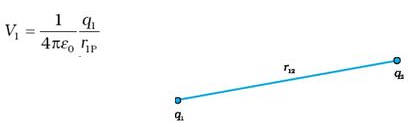
where r1P is the distance of a point P in space from the location of q1. - From the definition of potential, work done in bringing charge q2 from infinity to the point r2 is q times the potential at r2 due to q1:
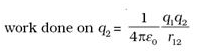
where r12 is the distance between points 1 and 2. - If q1q2 > 0, Potential energy is positive. For unlike charges (q1 q2 < 0), the electrostatic force is attractive.
- Potential energy of a system of three charges q1, qand q located at r1, r2, r, respectively. To bring q first from infinity to r1, no work is required. Next bring q2 from infinity to r2. As before, work done in this step is

- The total work done in assembling the charges at the given locations is obtained by adding the work done in different steps,
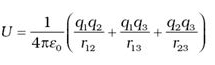
The document Relation between Electric Field, Potential & Potential Energy of a System of Charges | Physics for JAMB is a part of the JAMB Course Physics for JAMB.
All you need of JAMB at this link: JAMB
|
263 videos|252 docs|237 tests
|
FAQs on Relation between Electric Field, Potential & Potential Energy of a System of Charges - Physics for JAMB
| 1. What is the relationship between electric field and electric potential? |  |
Ans. The electric field is related to the electric potential by the equation E = -∇V, where E is the electric field vector, V is the electric potential, and ∇ is the gradient operator. This means that the electric field is the negative gradient of the electric potential.
| 2. How is potential energy related to a system of charges? |  |
Ans. The potential energy of a system of charges is related to the electric potential by the equation U = qV, where U is the potential energy, q is the charge, and V is the electric potential. This equation implies that the potential energy of a charge is equal to the product of its charge and the electric potential at its location.
| 3. What is the significance of electric potential in a system of charges? |  |
Ans. The electric potential in a system of charges determines the potential energy of the charges. It provides information about the distribution of electric potential throughout the system, which in turn affects the behavior of the charges and the electric field. By studying the electric potential, we can understand the forces and interactions between charges in the system.
| 4. How does the electric field affect the electric potential? |  |
Ans. The electric field determines the rate of change of electric potential in a system. If the electric field is stronger, the electric potential changes more rapidly, indicating a larger change in potential energy. Conversely, a weaker electric field leads to a slower change in electric potential. The electric field and electric potential are closely related, with the electric field being the negative gradient of the electric potential.
| 5. Can the electric potential exist without an electric field? |  |
Ans. No, the electric potential cannot exist without an electric field. The electric potential is a scalar quantity that is derived from the electric field. It represents the electric potential energy per unit charge at a given point in space. Without an electric field, there would be no electric potential as there would be no force or potential energy associated with the charges. The electric field is necessary to create and sustain the electric potential.
Related Searches





















