DC Pandey Solutions: Measurement & Errors | Physics Class 11 - NEET PDF Download
| Table of contents |

|
| Single Correct Option |

|
| More than One Correct Options |

|
| Assertion and Reason |

|
| Match the Columns |

|
The DC Pandey Solutions for Physics is a crucial book for Class 11 and 12 students. In the JEE physics community, DC Pandey is well-known among writers like HC Verma and Igor Irodov. Toppers of JEE exam also recommend this book. The book is divided into theory and numerical sections with solved examples and various practice questions. However, this book's primary emphasis is on the numerical side, and students are given a variety of practice problems to choose from. Additionally, every chapter of this book has problems of varying degrees of difficulty. EduRev provides solutions for all chapters of DC Pandey.
Single Correct Option
Q1. The percentage error in the measurement of mass and speed are 2% and 3% respectively. The error in the estimate of kinetic energy obtained by measuring mass and speed will be
(a) 12%
(b) 10%
(c) 8%
(d) 2%
Ans. (c)
We know that,
Kinetic energy
Fractional error in estimating Kinetic energy can be written as
ΔK / K=Δm / m + 2Δv / v
From this , Percentage error in estimating kinetic energy can be written as,
ΔK / K × 100=(Δm / m × 100) + 2(Δv / v × 100))
In words, we can say that,
Percentage error in estimating Kinetic energy = Percentage error in measuring mass + 2 × Percentage error in measuring speed.
∴ From the data given in the question,
Maximum error in estimating Kinetic energy =2 + 2(3) = 8%
∴ Maximum error = 2% + 2 (3%)
In the estimate of, kinetic energy (K) = 8%
Q2: The density of a cube is measured by measuring its mass and the len h of its sides. If the maximum error in the measurement of mass and length are 4% and 3% respectively, the maximum error in the measurement of density will be
(a) 7%
(b) 9%
(c) 12%
(d) 13%
Ans. (d)
- We first need to know about the relative error and the maximum error. Then we can easily solve this type of problem.
- Relative error is the ratio of the magnitude of error to the actual value of the physical quantity. Like relative error in mass is given by Δm / m where Δm is the magnitude of the error that is Δm = m(actual) - m(measured)
- Now, maximum error means that whenever two relative errors are together, they will be added but not subtracted.
∴
= 4% + 3(3%)
= 13%
Q3: Let g be the acceleration due to gravity at the earth’s surface and K the rotational kinetic energy of the earth. Suppose the earth’s radius decreases by 2%. Keeping all other quantities constant, then
(a) g increases by 2% and K increases by 2%
(b) g increases by 4% and K increases by 4%
(c) g decreases by 4% and K decrease by 2%
(d) g decreases by 2% and K decrease by 4%
Ans. (b)
∴ Decrease in R (radius) by 2% woud increase g by 4% and decrease K (rotational kinetic energy) by 4%.
Q4: By what percentage should the pressure of a given mass of gas be increased, so atorease its volume by 10% at a constant temperature?
(a) 11.1%
(b) 10.1%
(c) 9.1%
(d) 8.1%
Ans. (a)
According to Boyle's law, p1V1 = p2V2
⇒
∴ Percentage increase in pressure = 100/9
= 11.1
Q5: If the error in the measurement of the momentum of a particle is (+100%) Then, the error in the measurement of kinetic energy is
(a) 400%
(b) 300%
(c) 100%
(d) 200%
Ans. (b)
Since error in measurement of momentum is + 100%.
∴ p1 = p, p2 = 2p

Q6: The number of significant figures in 3400 is
(a) 7
(b) 6
(c) 12
(d) 2
Ans. (d)
Trailing zeros in a whole number with no decimal shown are NOT significant.
∴ Number of significant figures = 2
Q7: The length and breadth of a metal sheet are 3.124 m and 3.002 m respectively. The area of this sheet upto correct significant figure is
(a) 9.378 m2
(b) 9.37 m2
(c) 9.378248 m2
(d) 9.3782 m2
Ans. (a)
A = l x b = 3.124 m x 3.002 m
= 9.378248 m2When multiplying or dividing two or more numbers, count the significant figures in each of the original numbers. Take the smallest of the numbers of significant figures. The product or quotient will have that minimum number of significant figures. The number of significant figures in 3.124 is 4 and in 3.002 is also 4. Therefore, the minimum number of significant figures is 4.
Rounding off 9.378248 to 4 significant figures = 9.378 m2
Q8: The length, breadth, and thickness of a block are given by l = 12 cm, b = 6 cm and t =2.45 cm. The volume of the block according to the idea of significant figures should be
(a) 1 x 102 cm3
(b) 2 x 102 cm3
(c) 1.763 x 102 cm3
(d) None of these
Ans. (b)
V = l x b x t
V = 12 cm x 6 cm x 2.45 cmV = 176.4 cm2
= 1.764 x 102 cm3
When multiplying or dividing two or more numbers, count the significant figures in each of the original numbers. Take the smallest of the numbers of significant figures. The product or quotient will have that minimum number of significant figures. The number of significant figures in 12 is 2, 6 is 1 and 2.45 is 3. Therefore, the minimum number of significant figures is 1.
Rounding off 1.764 x 102 cm3 to 1 significant figure = 2 x 102 cm3.
Q9: If the separation between the screen and point source is increased by 2%. What would be the effect on the intensity?
(a) increases by 4%
(b) increases by 2%
(c) decreases by 2%
(d) decreases by 4%
Ans. (d)
Intensity formula,
i.e., Ir2 = constant
i.e., if 'r' is increased by 2%,
the intensity will decrease by 4%.
Q.10: The significant figures in the number 6.0023 are
(a) 2
(b) 5
(c) 4
(d) 1
Ans. (b)
Number of significant figures in 6.0023 are 5 because all the zeroes between two non zero digit are counted towards significant figures.
Q11: If the error in the measurement of the radius of a sphere is 1%, what will be the error in the measurement of volume?
(a) 1%
(b) 1/3 %
(c) 3%
(d) 10%
Ans. (c)
= 3(1%)
= 3%
Q12: The volume of a cube in m3 is equal to the surface area of the cube in m2. The volume of the cube is
(a) 64 m3
(b) 216 m3
(c) 512 m3
(d) 196 m3
Ans. (b)
Let a be the side of the cube.
Therefore, Volume of cube = a3
Surface area of the cube = 6a2
Now volume of the cube = surface area of the cube
a3 = 6a2 (given)
∴ a = 6
⇒ V = 63 = 216 m3
Q13: Charge on the capacitor is given by  where α and β are constants, t = time, I = current, ΔV = potential difference. The dimensions of β/α are same as the dimensions of
where α and β are constants, t = time, I = current, ΔV = potential difference. The dimensions of β/α are same as the dimensions of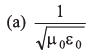
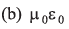
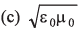
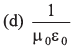
Ans. (a)
(given)
We know that
Q = It
⇒
Q14: A physical quantity A is dependent on the other four physical quantities p, q, r, and s as given by 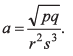 The percentage error of measurement in p, q, r, and s are 1%, 3%, 0.5%, and 0.33% respectively, then the maximum percentage error in A is
The percentage error of measurement in p, q, r, and s are 1%, 3%, 0.5%, and 0.33% respectively, then the maximum percentage error in A is
(a) 2%
(b) 0%
(c) 4%
(d) 3%
Ans. (c)
Q15: The distance moved by the screw of a screw gauge is 2 mm in four rotations and there are 50 divisions on its cap. When nothing is put between its jaws, the 30th division of circular scale coincides with the reference line, with zero of the circular scale lying above the reference line. When a plate is placed between the jaws, the main scale reads 2 divisions and the the circular scale reads 20 divisions. The thickness of the plate is
(a) 0.9 mm
(b) 1.2 mm
(c) 1.4 mm
(d) 1.5 mm
Ans. (d)
Least count of main scale
= 2mm/4 = 0.5 mm
= 0.1 mm Zero error = - 30 x 0.01 mm = -0.3 mm
(–ive sign, zero of circular scale is lying above observed reading of plate thick)
= 2 MSR + 20 CSR
= (2 × 0.5 mm) + (20 × 0.01 mm) = 1 mm + 0.2 mm = 1.2 mm.
Plate thickness (corrected reading)
= observed reading - zero error = 1.2 mm + 0.3 mm = 1.5 mm
More than One Correct Options
Q.1. Given, 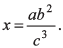 If the percentage errors in a, b and c are + 1%, ± 4%, and + 2% respectively.
If the percentage errors in a, b and c are + 1%, ± 4%, and + 2% respectively.
(a) The percentage error in x can be +13%
(b) The percentage error in x can be +7%
(c) The percentage error in x can be +18%
(d) The percentage error in x can be +19%
Ans. (a) & (b)
Maximum percentage error in x:
= 1 (% error in a) + 2 (% error in b) +3 (% error in c)
= 15%
Assertion and Reason
Directions: Choose the correct option.
(a) If both Assertion and Reason are true and the Reason is the correct explanation of the Assertion.
(b) If both Assertion and Reason are true but Reason is not the correct explanation of Assertion.
(c) If Assertion is true, but the Reason is false.
(d) If the Assertion is false but the Reason is true.
Assertion: A screw gauge having a smaller value of pitch has greater accuracy.
Reason: The least count of screw gauge is directly proportional to the number of divisions on a circular scale.
Ans. (a)
► Least count of screw gauge
► Less the value of pitch, less will be least count of screw gauge leading to len uncertainty that is more accuracy in the measurement.
Thus, assertion is true.
► From the above relation we conclude that least count of screw gauge is inversely proportional to the number of divisions of circular scale.
Thus reason is false.
Match the Columns
Q.1. Match the following two columns.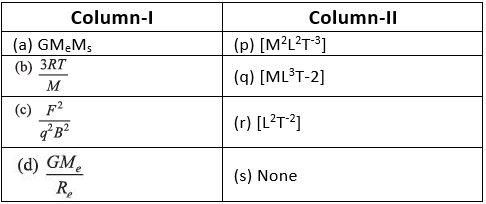
Ans. (a) → q (b) → r (c) → r (d) → r
(d)
⇒
= [L2 T–2]
∴ (d) → (r)
|
97 videos|378 docs|103 tests
|
FAQs on DC Pandey Solutions: Measurement & Errors - Physics Class 11 - NEET
| 1. What are the fundamental concepts of measurement in physics? |  |
| 2. How do systematic and random errors differ in measurements? |  |
| 3. What is the importance of significant figures in measurement? |  |
| 4. How can one minimize errors in experimental measurements? |  |
| 5. What role does the concept of uncertainty play in measurement? |  |

|
Explore Courses for NEET exam
|

|












 (given)
(given)

































