Section - 1
For each of the following pairs of fractions, decide which fraction is larger.
Ques 1: 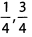
Ans: The denominators are the same, but the numerator of 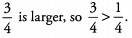
Ques 2: 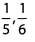
Ans: The numerators are the same, but the denominator of 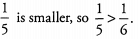
Ques 3: 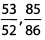
Ans: In the first fraction,53/52 , the numerator is bigger than the denominator, so the fraction is greater than 1. In the second fraction, 85/16 , the denominator is bigger than the numerator, so the fraction is less than 1. 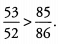
Section - 2
Add or subtract the following fractions. Fractions should be in their most simplified form.
Ques 4:
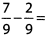
Ans:
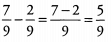
Ques 5:
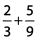
Ans:
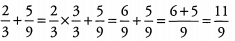
Ques 6:
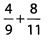
Ans:
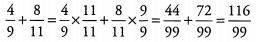
Ques 7: 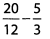
Ans:
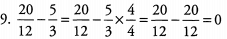
Ques 8: 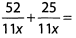
Ans: Because the denominators are the same, add the numerators and reduce.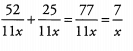
Ques 9: 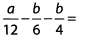
Ans: Find a common denominator and subtract. Because both 6 and 4 are factors of 12, 12 is the lowest common denominator.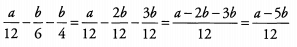
Ques 10: 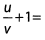
Ans: The common denominator of u/v and 1 is v.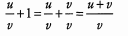
Section - 3
Convert the following improper fractions to mixed numbers.
Ques 11: 9/4
Ans: 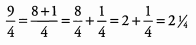
Ques 12: 31/7
Ans: 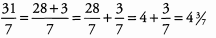
Ques 13: 47/15
Ans:
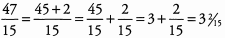
Ques 14: 70/20.
Ans: 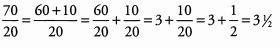
Section - 4
Convert the following mixed numbers to improper fractions.
Ques 15: 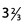
Ans: 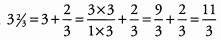
Ques 16: 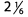
Ans: 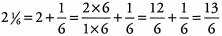
Ques 17: 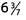
Ans: 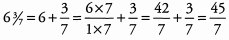
Ques 18: 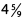
Ans:
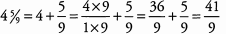
Ques 19: 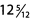
Ans:
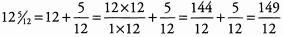
Section - 5
Simplify the following expressions.
Ques 20: 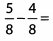
Ans: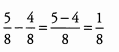
Ques 21: 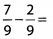
Ans: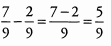
Ques 22: 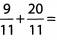
Ans: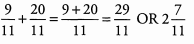
Ques 23: 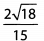
Ans: We begin by simplifying the square root in the numerator. When simplifying a square root, always look for factors that are perfect squares; in this example, we have 18 = 2 x 9 = 2 x 32. Therefore: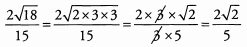
Ques 24: 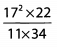
Ans:
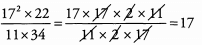
Ques 25: 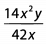
Ans:
Ques 26: 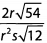
Ans: To begin, we simplify the square roots in the numerator and denominator by looking for factors that have pairs: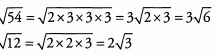
Because the numbers remaining inside the square roots have a factor of 3 in common, we can simplify even further: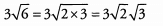
Therefore: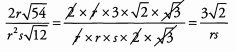
Ques 27: 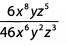
Ans: There are several good ways to simplify a fraction with variables raised to powers. One approach is to use exponent rules to rewrite the expression so that the cancelations are more clear: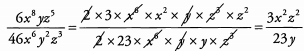
Alternatively, we can consider only one variable at a time and use other exponent rules to simplify: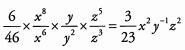
To combine these into one fraction, we can put x2 and z1 in the numerator, 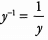
Place y in the denominator.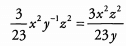
Section - 6
Multiply or divide the following fractions. Fractions should be in their most simplified form.
Ques 28: 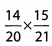
Ans: 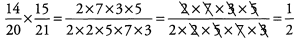
Ques 29: 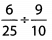
Ans: 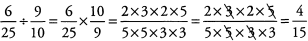
Ques 30: 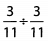
Ans: 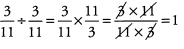
Ques 31: 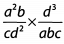
Ans: Before multiplying the fractions, look to cancel common factors.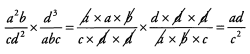
Ques 32: 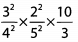
Ans: Before multiplying the fractions, look to cancel common factors.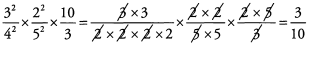
Ques 33: 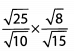
Ans: Begin by simplifying the roots.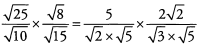
√2 can be canceled from the numerator and denominator. Also note that √5 appears twice in the denominator, and 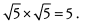

Ques 34: 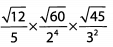
Ans: Begin by simplifying the roots.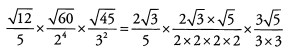
Look to cancel common factors before multiplying. Remember you can cancel across fractions because they are being multiplied.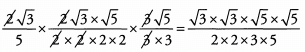
Now we can combine the roots in the numerator.
Section - 7
Simplify the following fractions.
Ques 35: 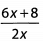
Ans: When the numerator of a fraction consists of two or more terms added together, but the denominator is a single term, we can split the fraction into two fractions with a common denominator and then simplify further: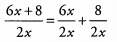
Now we need to simplify both fractions.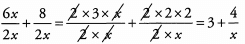
If you left the expressions as one fraction, then you could have factored a 2 out of each term in the expression: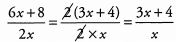
Either version is correct.
Ques 36: 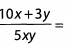
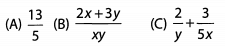
Ans: We can split this fraction into two fractions with a common denominator of 5xy and then simplify further: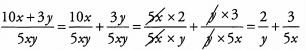
Now we have a match. The correct answer is (C).
Ques 37: 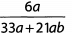
Ans: We must be careful when dealing with addition or subtraction in the denominator; the best we can do is identify factors common to all terms and cancel these. Every term within the fraction contains 3a as a factor: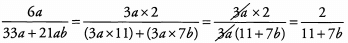
Ques 38: 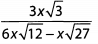
Ans: We begin by simplifying the square roots in the denominator: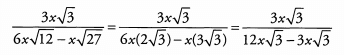
Because the subtraction is taking place in the denominator, we must identify common factors and cancel. These terms have a common factor of 3x√3 . Factor 3x√3 out of the denominator.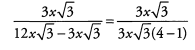
Now we can cancel 3x√3 from the numerator and denominator.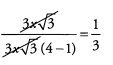
Section - 8
Simplify the following expressions. Final answers should be in their most simplified forms.Ques 39:
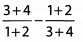
Ans: Begin by simplifying each fraction.

Because 3 and 7 share no common factors, the least common denominator is 3 x 7 = 21.
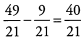
Ques 40:
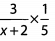
Ans:
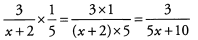
Ques 41:
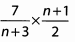
Ans:
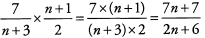
Ques 42:
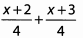
Ans:
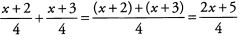
Ques 43:
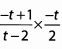
Ans:
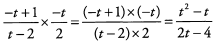
Ques 44:

Ans: When subtracting fractions with more than one term in the numerator, put the subtracted term in parentheses to remind yourself to distribute the negative:
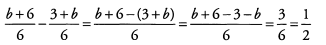
Section - 9
Match the following expressions to their simplified forms.Ques 45:

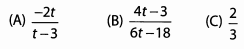
Ans: Begin by breaking down the fractions so that we can reduce common factors before we multiply. Remember that you can cancel across fractions because they’re multiplied.
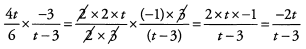
The answer is (A).
Ques 46:
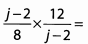
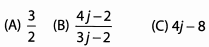
Ans: Begin by looking for common factors to cancel before we multiply.

Because (j - 2) is a factor of both the numerator and denominator, we can cancel it along with other common factors.
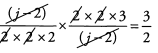
The answer is (A).
Ques 47:
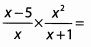

Ans: Break down each fraction and look for common denominators.
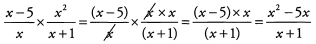
The answer is A.
Section - 10:
Simplify the following complex fractions.Ques 48:
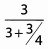
Ans: Begin by simplifying the denominator.
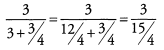
Dividing by (15/4) is the same as multiplying by (4/15).
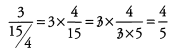
Ques 49:
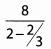
Ans: Begin by simplifying the denominator.
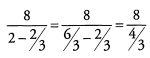
Now we can divide 8 by the fraction (4/3), which is the same as multiplying by (3/4).
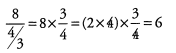
Ques 50:
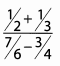
Ans: To begin, simplify the numerator and the denominator.
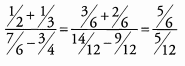
Now we can divide.
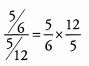
Simplify before you multiply.
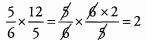
FAQs on Fractions: Solved Examples - GRE
| 1. What are fractions? |  |
| 2. How do you add fractions? |  |
| 3. Can fractions be added if they have different denominators? |  |
| 4. How do you simplify fractions? |  |
| 5. Can fractions be multiplied and divided? |  |














