ICAI Notes- Equations and Matrices- 2 | Quantitative Aptitude for CA Foundation PDF Download
MATRICES
LEARNING OBJECTIVES :
At the end of this chapter, you will be able to:
- Definition of Matrix
- Types of Matrix
- Addition and Subtraction of Matrix
- Multiplication of Matrices
- Transpose of Matrix
- Inverse of a Square Matrix
- Adjoint of a Square Matrix
- System of Linear Equations
- Cramer’s Rule (Determinant Method)
INTRODUCTION
Matrices applications are used in Business, Finance and Economics. Matrices applications are helpful to solve the linear equations with the help of this cost estimation, sales projection, etc., can be predicted. In this chapter, we shall find it interesting fundamental applications of matrices.
Matrix:
Ram, Sita and Laxman are three friends. Ram has 5 books, 3 pencils and 2 pens. Sita has 10 books, 8 pencils and 5 pens. Laxman has 15 books, 10 pencils and 2 pens. The above information about three friends can be represented in the following form:
| Books | Pencil | Pen | |
| Ram | 5 | 3 | 2 |
| Sita | 10 | 8 | 5 |
| Laxman | 5 | 10 | 2 |
We can express the above information in the following form: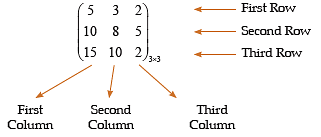
An arrangement or display of information in the above form is called a matrix.
Matrix (Definition)
A rectangular array of numbers (real/complex) denoted by: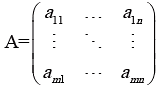
A is rectangular matrix with m rows and n columns. The numbers aij, i = 1,2 ……..m; j = 1,2,…..n of this array are called its elements aij, is associated. We shall denote a matrix either using by using brackets
[ ]; or ( ).
Notes:
- It is to be noted that a matrix is just an arrangement of elements without any value in rows and columns.
- The plural matrix is matrices.
- It is to be noted that a matrix is just an arrangement of elements without any value in rows and columns.
Order of a Matrix: A matrix A with m rows and n columns is called a matrix of order (m, n) or m × n (read as m by n).
Consider the matrix 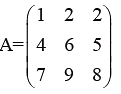
It is a matrix of order 3 × 3. Here the 9 occurs in the third row and second column. The elements 5 occurs in the second row and third column. Thus in notations we may write: a32 = 9 and a23 = 5.
TYPES OF MATRICES
Row Matrix:
A matrix which has only one row is called a row matrix or row vector.
The matrices of the type [a1, a2, a3 ……..,an]; [1, 2, 5] are examples of row matrices.
Column Matrix:
A matrix which has only one column is called a column matrix or a column vector.
The matrices are of the types 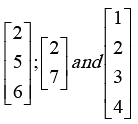 are examples of column.
are examples of column.
Zero Matrix or Null Matrix:
If every element of a m × n matrix is zero, the matrix is called zero matrix or null matrix of order (m, n) and it is denoted by : Omn. Thus [0, 0]; 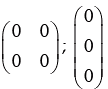 are all zero matrices, but all of matrices,
are all zero matrices, but all of matrices,
Square Matrix and Rectangular Matrix: If the number of rows and columns in a matrix are same, such a matrix is called a square matrix; otherwise it is called a rectangular matrix.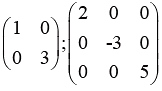 are examples of square matrix are zero except on the leading diagonal, then it is called diagonal matrix.
are examples of square matrix are zero except on the leading diagonal, then it is called diagonal matrix.
Thus, if 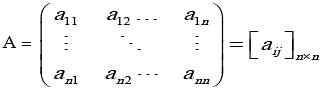
Is an n × n matrix, then the diagonal matrix obtained from it will be following type:
Diagonal Matrix = 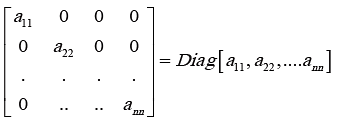
Scalar Matrix:
A diagonal matrix whose leading diagonal elements are all equal is called a scalar matrix, for example,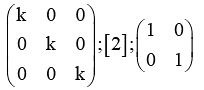
Unit Matrix:
A scalar matrix whose diagonal elements are equal to unity is called unit matrix and it is denoted by In×n, if it is order of order n .For example,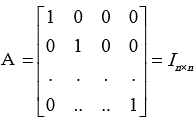
Upper triangle matrix:
A matrix is known as upper triangular matrix if all the elements below the leading diagonal are zero.
For example.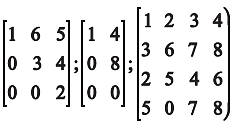
Lower Triangular Matrix:
A matrix is known as lower triangular matrix if all the elements above the leading diagonal are zero.
For example.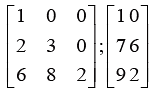
Sub Matrix:
The matrix obtained by deleting one or more rows or columns or both of a matrix is called its sub matrix. For example
The sub matrix is obtained by deleting second row and the second column from matrix A.
Equal Matrices:
Two matrices A=[aij] and B=[bij] are said to be equal if they satisfy the following two conditions.
(i) The order of both the matrices is same;
(ii) Corresponding elements in both the matrices are equal i.e.,
aij = bij (i = 1,2,…..m and j=1,2…….n)
ALGEBRA OF MATRICES
Addition and Subtraction of matrices: Let A and B be two matrices of the same order. Then the addition of A and B, denoted by A+B, is the matrix obtained by adding corresponding entries of A and similarly to subtract two matrices we just subtract their corresponding elements.
Thus, if A = (aij)m×n and B = (bij)m×n, then
A+B= (aij + bij)m×n
Remark: We can add two matrices of the same order. If they are of the same order, we say they are comfortable for addition. Also, the order of the matrices is the same as that of the two original matrices.
Property: If A, B, C are matrices of same order, then
(i) A + B = B + A (Commutative Law)
(ii) (A + B) + C = A + (B + C) (Associative Law)
(iii) K (A + B) = K.A + K.B, where m is constant
Example 1:
Negative of a Matrix: If A is any matrix, the negative of A is denoted by
Scalar Multiplication
The multiplication of a matrix by scalar k implies the multiplication of every element.
Example 2:
Solution: Then k 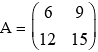
Multiplication of two matrices.
The product A B of two matrices A and B defined only if the number of columns in Matrix A is equal to the number of rows in Matrix B.
Properties of matrix Multiplication:
(i) Matrix multiplication is not commutative in general, i.e. AB ≠ BA.
(ii) Matrix multiplication is associative (AB) C = A(BC), where both sides are defined.
(iii) Multiplication distributes over addition of Matrices i.e.,
(a) A (B + C) = AB + AC
(b) (A + B) C = AC + BC
(iv) If A, B and C are three matrices such that AB = AC , then the general B ≠ C.
(v) If A is m×n matrix and O is an n × p null matrix, then AO = O, A= O
(vi) If A is a square matrix and I is a unit matrix of the same order, then AI = IA = O
(vii) Product of the two no-zero matrices is non zero matrix.
Example: 3 if 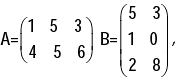 find AB
find AB
Solution: 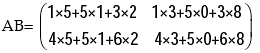
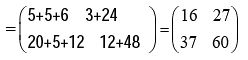
Example 4: The annual sale volume of three products X , Y , Z whose sale prices per unit are ₹ 3.50, ₹2.75 , ₹ 1.50 respectively. In two different market I and II are shown below.
| Market | Product | ||
| X | Y | Z | |
| I | 6000 | 9000 | 13000 |
| II | 12000 | 6000 | 17000 |
Find the total revenue in each market with the help of matrices.
Solution: Let P denotes the column matrix of prices and S denote the rectangular matrix of sale of volumes of three different commodities at three different markets. Then,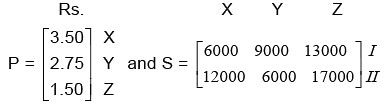
Total revenue in markets I and II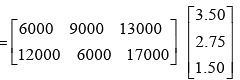

Transpose of Matrix: The matrix is obtained by interchanging rows and columns of a matrix A is called its transpose. Transpose of a matrix by AT or A’.
Symbolically, if A=[aij] and A’=[bij]
Then aij=bij
Example:
Let A= 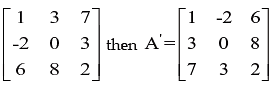
Properties of transpose of a Matrix:
(1) A matrix is transpose of its matrix i.e. A = (A’)’.
(2) The transpose of the sum of the two matrices is the sum of their transpose matrices, i.e.
(A + B)’= A’ + B’
(3) Transpose of a multiplication of a matrix and constant number is equal to the multiplication of the constant number by the transpose of matrix, i.e. (KA)’ = K.A’
(4) The transpose of the two matrices are equal to the product of their transpose in reverse order, i.e., (AB)’ = B’. A’
Symmetric Matrix: In any matrix if A is called symmetric then A’ = A.
Example 5: Let A = 
Here A’= A, A is called symmetric matrix.
Solution: Skew Symmetric matrix: Any matrix A is called skew symmetric. If A’=-A,
for a skew symmetric matric A = [aij], aij = – aij
Example 6: Find A2 , if 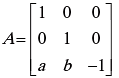
Solution: A2 = A.A = 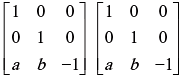
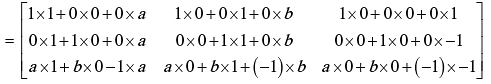

Example 7: (a) Show that the matrix 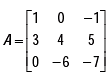 satisfi es the equation:
satisfi es the equation:
A3 + 2A2 - A- 20 I = 0 .
Solution: 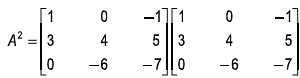
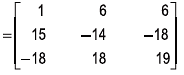
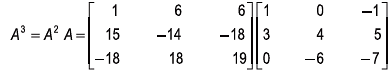

Now A3+2A2- A - 20I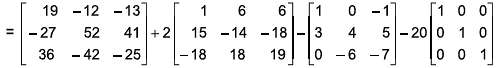
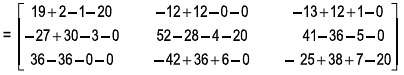

(b) If A = 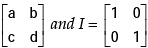 then show that A2 -(a+d)A = (bc - ad)I
then show that A2 -(a+d)A = (bc - ad)I
Solution: We may write,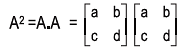
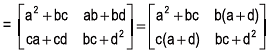
L.H.S. of the given equation = A2−(a+d)A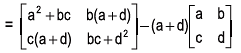
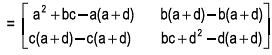
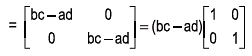
= (bc−ad) I = R.H.S.
Hence, A2 – (a + d) A = (bc–ad) I.
Example 8: If 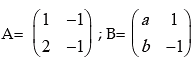 and (A+B)2 =A2 + B2, find the value of a and b
and (A+B)2 =A2 + B2, find the value of a and b
Solution:
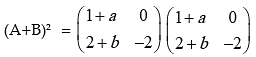
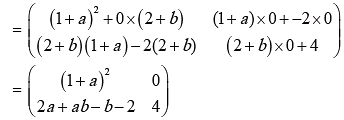
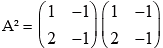
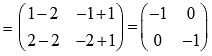
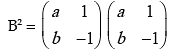
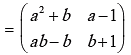
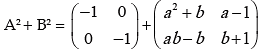
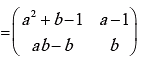
Now (A + B)2 = A2 + B2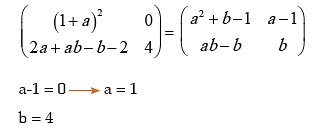
Example 9: A company employs 60 labourers from either of party A and B, comprising of persons in different age groups as under:
| Category | I (20-25 years) | II (26-30 years) | III (31-40 years) |
| Party A | 25 | 25 | 15 |
| Party B | 20 | 30 | 10 |
| Category | Rates |
| I | 1200 |
| II | 1000 |
| III | 600 |
Rate of Labour applicable to categories I, II and III are ₹1,200, ₹ 1,000 and ₹ 600 respectively. Using matrices, find which party is economically preferable over the other.
Solution:
| Category | I (20-25 years) | II (26-30 years) | III (31-40 years) |
| Party A | 25 | 25 | 15 |
| Party B | 20 | 30 | 10 |
Rates :
| Category | Rates |
| I | 1200 |
| II | 1000 |
| III | 600 |
Labour charges payble ton each party can be given by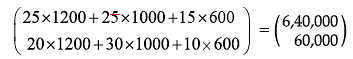
Therefore, Party B is more economical as compared to Party A.
Example 10: In a certain city there are 5 colleges and 20 schools. Each school has 3 peons, 1 clerk and 1 head-clerk, where a college has 5 peons, 3 clerks, 1 head. clerk and additional staff of a caretaker. The monthly salary of a employee is as follows.
| Peon | ₹ 1100 |
| Clerk | ₹ 1700 |
| Head-clerk | ₹ 3000 |
| Caretaker | ₹ 2500 |
Using matrix method, find the total monthly bill of each college.
Solution: Let us put the information in tabular form:
| Peon | Clerk | Head-clerk | Caretaker | |
| School | 3 | 1 | 1 | 0 |
| College | 5 | 3 | 1 | 1 |
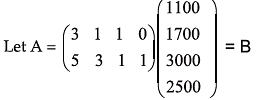
Therfore, The monthly bill for a school and a college is given as: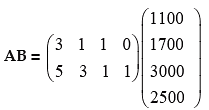
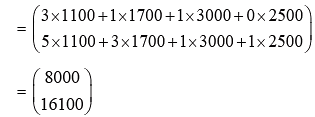
Therefore, the monthly bill for a school is ₹8,000 and for a college is ₹16,100
Example 11: There are two families A and B .There are 4 men, 6 women and 2 Children in a Family A and 2 men, 2 women, and 4 children in Family B .The recommended requirement of calories in Man: 2400, Woman : 1900, Child : 1800 and for proteins in Man: 55 gm, Woman: 45 gm and Child: 33 gm.
Solution: Represent the above information by matrices in using matrix multiplication method
Solution: The members of the two families can be represented by the 2 × 3 matrix.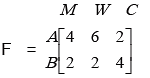
And the recommended daily requirement of calories and proteins for each member can be represented by the 3 × 2 matrix: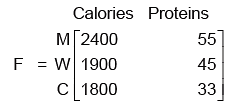
The total requirements of calories and proteins for each of the families is given by matrix multiplication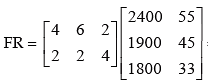
= 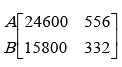
Hence finally A requires 24,600 calories and 556 gm proteins and Family B requires 15,800 calories and 332 gm proteins.
Example 12: Three firms A, B and C supplied 40, 35 and 25 truckloads of stones and 5, 8 truckloads of sand respectively to a contractor. If the costs of stone and sand are ₹1200 and ₹500 per truck load respectively, find total amount paid by the contractor to each of these firms, buy using matrix method.
Solution: The amount of stone and sand supplied to a contractor by three firms A, B and C can represented by using matrix method.
The cost per truck load of stone and stand can be represented by the column matrix.
Thus, the total amount paid by the contractor to each of these firms is given by the matrix product.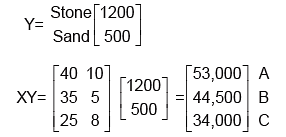
Hence the amount paid to firms A = ₹53,000; B = ₹44,500 and C = ₹ 34,000
DETERMINANTS
The determinant of a square matrix is a number which is associated with the square matrix. This number may be positive, negative or zero > the determinant of a square matrix A commonly denoted by det A or | A| or Δ. The matrices which are not square do not have determinants.
Determinants are quite useful to solving a system of linear equations. They are also equations. They are also helpful in expressing certain formulas.
The determinant of a (2 × 2) matrix A 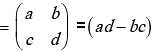
The determinant of (3 × 3) matrix, A 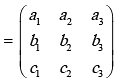
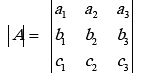
And its defined as 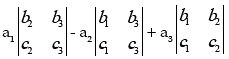
= a1 (b2c3-b3c2) – a2(b1c3-b3c1) + a3(b1c2-b2c1)
Minors and Cofactors of a Determinant:
Minor of the element of a determinant is the determinant of Mij by deleting ith row and jth column in which element is existing.
Cofactor of matrix A = (-1)i+j Mij , Where Mij = Minor of the element ith row and jth column.
Minors: Let us consider the determinant 
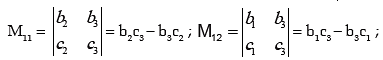
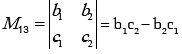

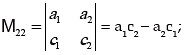
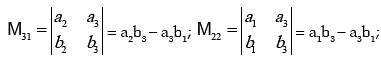
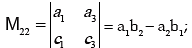
Cofactors
C11= (-1)1+1M11= M11, C12= (-1)1+2M12= -M21 ; C13= (-1)1+3M13= M13
C21= (-1)2+1M21= - M21 , C22= (-1)2+2M22= M22 ; C23= (-1)2+3M23= -M23
C31= (-1) 3+1M31= M31 , C32= (-1)3+2M32= -M32 ; C33= (-1)3+3M33= M33
The value of determinant can be defined in terms of cofactor matrix as
Δ = a11 c11 + a12 c12 + a13c13
or
Δ = a11 c11 + a21 c12 + a31 c13
Properties of Determinants:
1) The value of determinant remains unaltered interchanged if its rows or columns
interchanged.
2) The value of determinant change signs if any two rows (or columns) interchanges.
3) The value of determinant is zero if any two rows (any columns) then value of determinant
is equal to zero.
4) The value determinant becomes k times (where k is constant) if any row or columns
multiplied by k the value of determinant also multiplied by k.
5) The value of determinant is zero if any two rows (or column) are proportional then the
value of determinant is equal to zero.
6) If each element of any row (or column) is a sum of two numbers, the determinant can be
expressed as the sum of the determinants.
7) The value of determinant remains same if to any (or column) multiple of row (or column) is added or subtracted.
Singular and Non-Singular Matrices: Any Square Matrix A is singular, if | A | = 0 . The matrix is non-singular, if | A | ≠ 0 .
Example 13: If 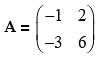 Prove that A is a singular matrix.
Prove that A is a singular matrix.
Solution: 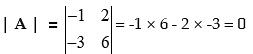
A is singular matrix.
Example 14: Find the determinant value of the following matrices.
Solution by definition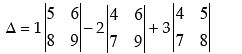
= 1(45 – 48) –2(36 – 42) + 3(32 – 35)
= -3 + 12 - 9 = 0
Adjoint Matrix: Adjoint of A Matrix is the transpose of the Cofactor Matrix
Example 15: Find the Adjoint of the Matrix.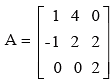
Solution:
The Co-factors of elements of 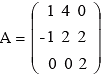 are calculated below
are calculated below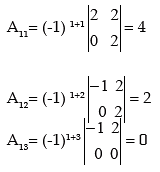
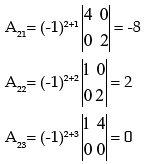
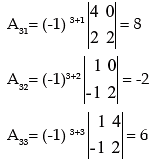

INVERSE OF A MATRIX
If A is a Square matrix and A ≠ 0 then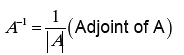
Example 16:
Solve the following system of equations by matrix inversion method :
2x + 8y + 5z = 5
X + y + z = (-2)
X + 2y – z = -2
Solution: The given system of equations can be written in the form, AX = B.
Where (A) = 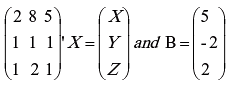
det (A)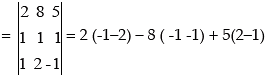
= -6 + 16 + 5
= 15 ≠ 0
Hence, the system has a unique solution as A is non-singular. The solution is given by
X = A-1B
To find A-1, we find the cofactors.
A11 = -3; A12 = + 2; A13 = 1, A21 = + 18; A22 =-7; A23 + 4; A31 = 3; A22 = +3; A33 = -6
Co-factor of 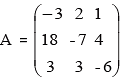
Adj: A = (co-factor A)T = 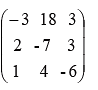
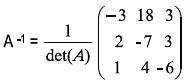
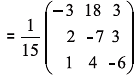
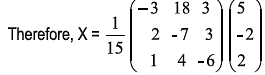

Hence, x = -3; y = 2 and z = -1
Example 17: Show that the matrix 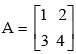 satisfies the equation
satisfies the equation
A2 –5A –2I = 0
Hence, deduce the value of A-1
Solution: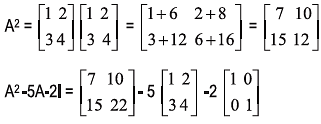
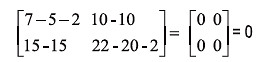
Since A2 – 5A – 2I = 0,
⇒A-1 (A2 – 5A – 2I) = 0
⇒ A-5I – 2A-1 = 0
⇒ 2A-1 = A – 5I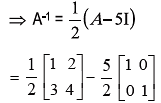
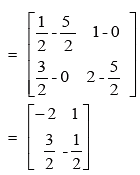
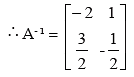
Example 18:
Fine the inverse of the matrix.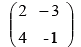
Solution: Hence, solve the system of equations.
2x – 3y = 3
4x – 11y = 11
Hence, Inverse of 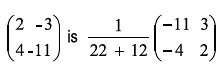

The given system of equations cab be written as
AX = B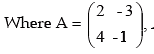
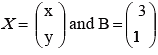
Therefore,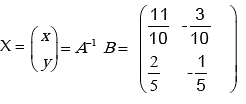

Hence x = 0, y = -1
Example 19: Using the inverse of the coef cient matrix, solve the following system of equations:
x + y + z = 3
x + 2y + 3z =4
x + 4y + 9z = 6
Solution: The given equation can be written as AX = B. Where 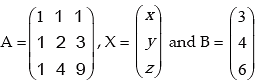
Since,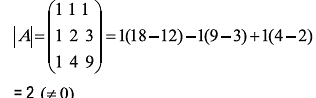
∴ The given equations are consistent, and the solution is given by X =A-1 B.
Let us find the cofactors:
A11 = 6; A12= -6; A13= 2; A21 = -5; A22 = 8; A23 = -3
A31 = 1; A32 = - 2 and A33 = 1
Then Cof.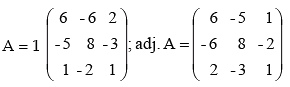
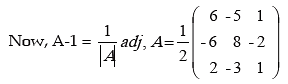
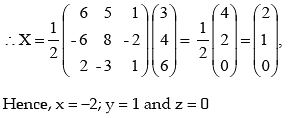
SOLUTION OF LINEAR EQUATIONS IN THREE VARIABLES (CRAMER’S RULE)
The solution of equations
a11 + a12y + a13z = d1
a21 + a22y + a23z = d2
a31 + a32y + a33z = d3
is give by 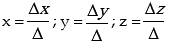
provided Δ≠0, and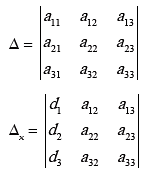
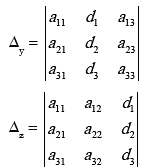
Notes : 1) If Δ = 0; and Δx = 0, Δy = 0 , Δz= 0; then the given equations will have in nite solutions and equations will be dependent.
2) If Δ = 0; and at least Δx , Δy = 0 , Δz; is not zero then the equations will have solution and the equations have no solution and the equations are said to be inconsistent.
Example 20: Solve the equations:
1) 2x – y + z = 4
X + 3y + 2z = 12
3x + 2y + 3z = 16
Solution: Considering the equations:
2x – y + z = 4
X + 3y + 2z = 12
3x + 2y + 3z = 16
By using Cramer’s Rule, the solution of the equations are given below: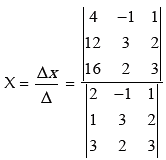
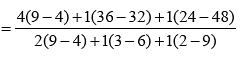
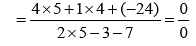
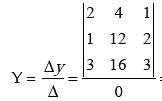
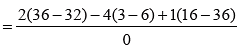
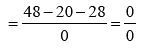
Since Δ = 0; Δx= 0, Δy= 0 and Δz= 0,
There the equations are dependent and will have infinite solutions;
Example 21:
x + y + 3z = 6
x – 3y – 3z = –4
5x – 3y + 3z = 8
Solution: By applying Cramer’s rule, we get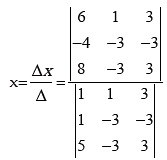
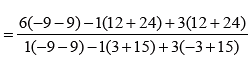
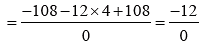
Since Δx ≠ 0 and Δ = 0, therefore the system of equations are inconsistent.
Example 22: The given equations are:
x + y – z = –2
3x + 2y + 3z =13
2x + 7y + 4z = 31
Solution: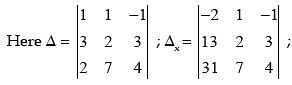
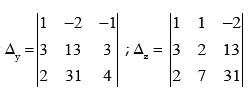
Δ = 1 (8 – 21) –1 (12 – 6) –1(21 – 4) = –13–6–17= –36
Δx = –2 (8 – 21) –1 (52 – 93) –1(91 – 62) = 26 + 41 – 29 = 38
Δy = 1 (52 – 93) +2 (12 – 6) –1(93 – 26) =–14 + 12 – 67= –96
Δz = 1 (62 – 91) –1 (93 – 26) –1(21 – 4) = –13 – 6 – 17 = –36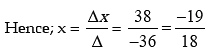
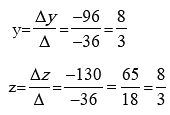
|
114 videos|164 docs|98 tests
|
FAQs on ICAI Notes- Equations and Matrices- 2 - Quantitative Aptitude for CA Foundation
| 1. What are the basic operations that can be performed on matrices? |  |
| 2. How do you determine the order of a matrix? |  |
| 3. How are equations solved using matrices? |  |
| 4. What is the determinant of a matrix? |  |
| 5. How does matrix multiplication work? |  |
|
114 videos|164 docs|98 tests
|

|
Explore Courses for CA Foundation exam
|

|

















