ICAI Notes: Time Value of Money- 3 - CA Foundation PDF Download
PERPETUITY
Perpetuity is an annuity in which the periodic payments or receipts begin on a fixed date and continue indefinitely or perpetually. Fixed coupon payments on permanently invested
(irredeemable) sums of money are prime examples of perpetuities.
The formula for evaluating perpetuity is relatively straight forward. Two points which are
important to understand in this regard are:.
(a) The value of the perpetuity is finite because receipts that are anticipated far in the future have extremely low present value (today’s value of the future cash flows).
(b) Additionally, because the principal is never repaid, there is no present value for the
principal.
Therefore, the price of perpetuity is simply the coupon amount over the appropriate discount rate or yield.
4.11.1 Calculation of multi period perpetuity:
The formula for determining the present value of multi-period perpetuity is as follows: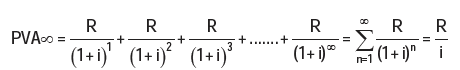
Where:
R = the payment or receipt each period
i = the interest rate per payment or receipt period
Example 41: Ramesh wants to retire and receive ₹ 3,000 a month. He wants to pass this
monthly payment to future generations after his death. He can earn an interest of 8%
compounded annually. How much will he need to set aside to achieve his perpetuity goal?
Solution:
R = ₹3,000
i = 0.08/12 or 0.00667
Substituting these values in the above formula, we get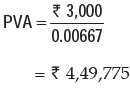
If he wanted the payments to start today, he must increase the size of the funds to handle the first payment. This is achieved by depositing ₹ 4,52,775 (PV of normal perpetuity + perpetuity received in the beginning = 4,49,775 + 3,000) which provides the immediate payment of ₹3,000 and leaves ₹4,49,775 in the fund to provide the future ₹3,000 payments.
4.11.2 Calculation of Growing Perpetuity:
A stream of cash flows that grows at a constant rate forever is known as growing perpetuity.
The formula for determining the present value of growing perpetuity is as follows: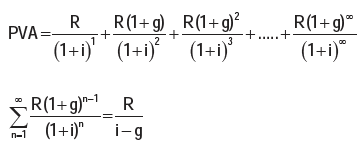
Example 42: Assuming that the discount rate is 7% per annum, how much would you pay to receive ₹50, growing at 5%, annually, forever?
Solution: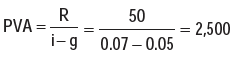
Calculating Rate of Return:
1) Calculating the rate of return provides important information that can be used for future
investments. For example, if you invested in a stock that showed a substantial gain after
several months of performance, you may decide to purchase more of that stock. If the
stock showed a continual loss, it may be wise to conduct research to find a better-performing stock.
2) calculating the rate of return is that it allows you to gauge your investment and decision making skills. Investments that create a gain or profit are great. However, if you continually make investments at a loss, then you may want to change your investment strategies. A great attribute of successful business people is knowing how and when to make investments, as is knowing when to change strategies. With a firm grasp of calculating the rate of return, you can manage and monitor your investments at various stages to determine the outcome of your investments. This leads to a higher level of confidence and the skills necessary to be a savvy investor.
Net Present Value Technique (NPV): The net present value technique is a discounted cash flow method that considers the time value of money in evaluating capital investments. An investment has cash flows throughout its life, and it is assumed that a rupee of cash flow in the early years of an investment is worth more than a rupee of cash flow in a later year.
The net present value method uses a specified discount rate to bring all subsequent net cash inflows after the initial investment to their present values (the time of the initial investment is year 0).
Determining Discount Rate
Theoretically, the discount rate or desired rate of return on an investment is the rate of return the firm would have earned by investing the same funds in the best available alternative investment that has the same risk. Determining the best alternative opportunity available is difficult in practical terms so rather that using the true opportunity cost, organizations often use an alternative measure for the desired rate of return. An organization may establish a minimum rate of return that all capital projects must meet; this minimum could be based on an industry average or the cost of other investment opportunities. Many organizations choose to use the overall cost of capital or Weighted Average Cost of Capital (WACC) that an organization has incurred in raising funds or expects to incur in raising the funds needed for an investment.
The net present value of a project is the amount, in current value of rupees, the investment
earns after paying cost of capital in each period.
NET PRESENT VALUE
Net present value = Present value of net cash inflow – Total net initial investment
Since it might be possible that some additional investment may also be required during the life time of the project then appropriate formula shall be:
Net present value = Present value of cash inflow – Present value of cash outflow
The steps to calculating net present value are:-
1. Determine the net cash inflow in each year of the investment.
2. Select the desired rate of return or discounting rate or Weighted Average Cost of Capital.
3. Find the discount factor for each year based on the desired rate of return selected.
4. Determine the present values of the net cash flows by multiplying the cash flows by
respective the discount factors of respective period called Present Value (PV) of Cash
flows
5. Total the amounts of all PVs of Cash Flows
Decision Rule:
If NPV ≥ 0 Accept the Proposal
If NPV ≤ 0 Reject the Proposal
Example 43: Compute the net present value for a project with a net investment of
₹1,00,000 and net cash flows year one is ₹55,000; for year two is ₹80,000 and for year
three is ₹15,000. Further, the company’s cost of capital is 10%?
[PVIF @ 10% for three years are 0.909, 0.826 and 0.751]
Solution:
| Year | Net Cash Flows | PVIF @ 10% | Discounted Cash Flows |
| 0 | (1,00,000) | 1.000 | (1,00,000) |
| 1 | 55000 | 0.909 | 49995 |
| 2 | 80000 | 0.826 | 66080 |
| 3 | 15000 | 0.751 | 11265 |
| Net Present Value | 27340 | ||
Recommendation: Since the net present value of the project is positive, the company should accept the project.
NOMINAL RATE OF RETURN
The nominal rate is the stated interest rate. If a bank pays 5% annually on a savings account, then 5% is the nominal interest rate. So if you deposit ₹ 100 for 1 year, you will receive ₹5 in interest. However, that ₹ 5 will probably be worth less at the end of the year than it would have been at the beginning. This is because inflation lowers the value of money. As goods, services, and assets, such as real estate, rise in price.
The nominal interest rate is conceptually the simplest type of interest rate. It is quite simply the stated interest rate of a given bond or loan. It is also defined as a stated interest rate. This interest works according to the simple interest and does not take into account the compounding periods.
Real Rate of Return: The real interest rate is so named because it states the “real” rate that
the lender or investor receives after inflation is factored in; that is, the interest rate that exceeds the inflation rate.
A comparison of real and nominal interest rates can therefore be summed up in this equation:
Nominal Rate of Return – Inflation = Real Rate of Return
Nominal Interest Rate = Real Interest Rate + Inflation
Effective Rate:
It is the actual equivalent annual rate of interest at which an investment grows in value when interest is credited more often than once a year. If interest is paid m times in a year it can be found by calculating: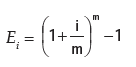
The chief advantage to knowing the difference between nominal, real and effective rates is
that it allows consumers to make better decisions about their loans and investments. A loan with frequent compounding periods will be more expensive than one that compounds annually
A bond that only pays a 1% real interest rate may not be worth investors’ time if they seek to grow their assets over time. These rates effectively reveal the true return that will be posted by a fixed-income investment and the true cost of borrowing for an individual or business. Effective and nominal interest rates allow banks to use the number that looks most advantageous to the consumer. When banks are charging interest, they advertise the nominal rate, which is lower and does not reflect how much interest the consumer would owe on the balance after a full year of compounding. On the other hand, with deposit accounts where banks are paying interest, they generally advertise the effective rate because it is higher than the nominal rate.
COMPOUND ANNUAL GROWTH RATE (CAGR)
Compounded Annual Growth Rate (CAGR) is a business and investing specific term for the
smoothed annualized gain of an investment over a given time periodic is not an accounting term, but remains widely used, particularly in growth industries or to compare the growth rates of two investments because CAGR dampens the effect of volatility of periodic returns that can render arithmetic means irrelevant. CAGR is often used to describe the growth over a period of time of some element of the business, for example revenue, units delivered, registered users, etc.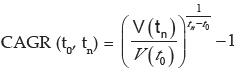
Where V(t0 ) = Beginning Period ; V( tn ) = End Period
Example: Suppose the revenues of a company for four years, V(t) in the above formula, have been
| Year | 2013 | 2014 | 2015 | 2016 |
| Revenues | 100 | 120 | 160 | 210 |
Calculate Compound annual Growth Rate.
Solution:
tn -t0 = 2016 - 2013 = 3
The CAGR revenues over the three-year period from the end of 2013 to the end of 20016 is CAGR (0, 3) 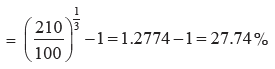
Applications: These are some of the common CAGR applications:
- Calculating average returns of investment funds.
- Demonstrating and comparing the performance of investment advisors.
- Comparing the historical returns of stocks with bonds or with a savings account.
- Forecasting future values based on the CAGR of a data series.
- Analyzing and communicating the behavior, over a series of years, of different business measures such as sales, market share, costs, customer satisfaction, and performance.
SUMMARY
- Time value of money: Time value of money means that the value of a unity of money is different in different time periods. The sum of money received in future is less valuable than it is today. In other words the present worth of money received after some time will be less than a money received today.
- Interest: Interest is the price paid by a borrower for the use of a lender’s money. If you borrow (or lend) some money from (or to) a person for a particular period you would pay (or receive) more money than your initial borrowing (or lending).
- Simple interest: is the interest computed on the principal for the entire period of borrowing.
I = Pit
A = P + I
I = A – P
Here, A = Accumulated amount (final value of an investment)
P = Principal (initial value of an investment)
i = Annual interest rate in decimal.
I = Amount of Interest
t = Time in years
Compound interest as the interest that accrues when earnings for each specified period
of time added to the principal thus increasing the principal base on which subsequent
interest is computed.
Formula for compound interest:
An = P ( 1 + i)n
where, i = Annual rate of interest
n = Number of conversion periods per year
Interest = An – P = P ( 1 + i )n – P
n is total conversions i.e. t x no. of conversions per year
Effective Rate of Interest: The effective interest rate can be computed directly by
following formula:
E = (1 + i)n– 1
Where E is the effective interest rate
i = actual interest rate in decimal
n = number of conversion period
⇒ Future value of a single cash flow can be computed by above formula. Replace A by
future value (F) and P by single cash flow (C.F.) therefore
F = C.F. (1 + i)n
⇒ Annuity can be defined as a sequence of periodic payments (or receipts) regularly over
a specified period of time.
Annuity may be of two types:
(i) Annuity regular: In annuity regular first payment/receipt takes place at the end of
first period.
(ii) Annuity Due or Annuity Immediate: When the first receipt or payment is made today
(at the beginning of the annuity) it is called annuity due or annuity immediate.
⇒ If A be the periodic payments, the future value A(n, i) of the annuity is given by
⇒Future value of an Annuity due/Annuity immediate = Future value of annuity regular
x (1+i) where i is the interest rate in decimal.
⇒ The present value P of the amount An due at the end of n period at the rate of i per
interest period may be obtained by solving for P the below given equation
⇒ Present value of annuity due or annuity immediate: Present value of annuity due/immediate for n years is the same as an annuity regular for (n-1) years plus an initial
receipt or payment in beginning of the period. Calculating the present value of annuity
due involves two steps.
Step 1: Compute the present value of annuity as if it were a annuity regular for one
period short.
Step 2: Add initial cash payment/receipt to the step 1 value.
⇒ Sinking Fund: It is the fund credited for a specified purpose by way of sequence of
periodic payments over a time period at a specified interest rate. Interest is compounded
at the end of every period. Sizeof the sinking fund deposit is computed from A = P.A(n,
i) where A is the amount to be saved the periodic payment, n the payment period
Annuity applications:
(a) Leasing: Leasing is a financial arrangement under which the owner of the asset
(lessor) allows the user of the asset (lessee) to use the asset for a defined period of
time (lease period) for a consideration (lease rental) payable over a given period of
time. This is a kind of taking an asset on rent.
(b) Capital Expenditure (investment decision): Capital expenditure means purchasing an asset (which results in outflows of money) today in anticipation of benefits (cash inflow) which would flow across the life of the investment.
(c) Valuation of Bond: A bond is a debt security in which the issuer owes the holder a
debt and is obliged to repay the principal and interest. Bonds are generally issued for
a fixed term longer than one year.
FAQs on ICAI Notes: Time Value of Money- 3 - CA Foundation
| 1. What is the concept of time value of money? |  |
| 2. How does time value of money affect investment decisions? |  |
| 3. What are the key components of time value of money? |  |
| 4. How can the time value of money be applied in personal finance? |  |
| 5. What are the limitations of the time value of money concept? |  |

|
Explore Courses for CA Foundation exam
|

|


















