Taylor's and Laurent Series | Basic Physics for IIT JAM PDF Download
A Taylor series is a series expansion of a function about a point. A one-dimensional Taylor series is an expansion of a real function f(x) about a point x=a is given by
f(x) = 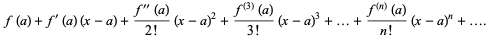 (1)
(1)
If a=0, the expansion is known as a Maclaurin series.
Taylor's theorem (actually discovered first by Gregory) states that any function satisfying certain conditions can be expressed as a Taylor series.
The Taylor (or more general) series of a function f(x) about a point  up to order
up to order  may be found using Series[f, {x, a, n}]. The nth term of a Taylor series of a function f can be computed in the Wolfram Language using Series Coefficient[f, {x, a, n}] and is given by the inverse Z-transform
may be found using Series[f, {x, a, n}]. The nth term of a Taylor series of a function f can be computed in the Wolfram Language using Series Coefficient[f, {x, a, n}] and is given by the inverse Z-transform
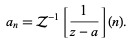 (2)
(2)
Taylor series of some common functions include
To derive the Taylor series of a function f(x), note that the integral of the (n+1)st derivative f(n+1) of f(x) from the point x0 to an arbitrary point x is given by
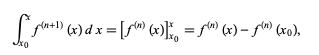 (9)
(9)
where f(n) (x0) is the nth derivative of f(x) evaluated at x0, and is therefore simply a constant. Now integrate a second time to obtain
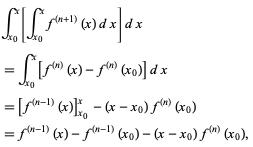 (10)
(10)
where f(k) (x0) is again a constant. Integrating a third time,
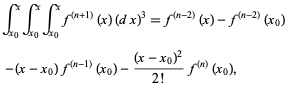 (11)
(11)
and continuing up to n+1 integrations then gives
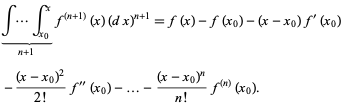 (12)
(12)
Rearranging then gives the one-dimensional Taylor series
Here, Rn is a remainder term known as the Lagrange remainder, which is given by
 (15)
(15)
Rewriting the repeated integral then gives
 (16)
(16)
Now, from the mean-value theorem for a function g(x), it must be true that
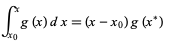 (17)
(17)
for some 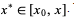 Therefore, integrating n+1 times gives the result
Therefore, integrating n+1 times gives the result
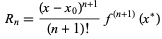 (18)
(18)
If f(z) is analytic throughout the annular region between and on the concentric circles K1 and k2 centered at z=a and of radii r1 and r2<r1 respectively, then there exists a unique series expansion in terms of positive and negative powers of (z-a),
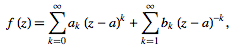 (19)
(19)
where
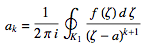 (20)
(20)
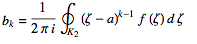 (21)
(21)
(Korn and Korn 1968, pp. 197-198).
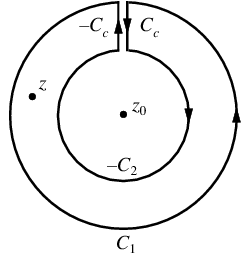
Let there be two circular contours c2 and c1, with the radius of c1 larger than that of c2. Let z0 be at the center of c1 and c2, and 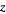 be between c1 and c2. Now create a cut line cc between c1 and c2, and integrate around the path
be between c1 and c2. Now create a cut line cc between c1 and c2, and integrate around the path 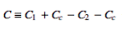 , so that the plus and minus contributions of cc cancel one another, as illustrated above. From the Cauchy integral formula,
, so that the plus and minus contributions of cc cancel one another, as illustrated above. From the Cauchy integral formula,
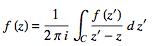 (22)
(22)
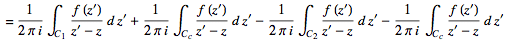 (23)
(23)
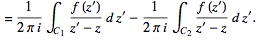 (24)
(24)
Now, since contributions from the cut line in opposite directions cancel out,
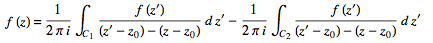 (25)
(25)
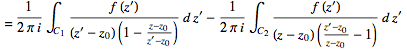 (26)
(26)
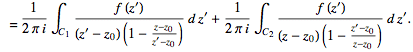 (27)
(27)
For the first integral,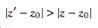 . For the second,
. For the second, 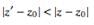 . Now use the Taylor series (valid for
. Now use the Taylor series (valid for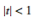 )
)
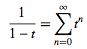 (28)
(28)
to obtain
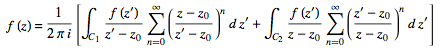 (29)
(29)
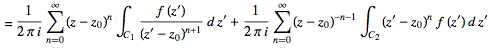 (30)
(30)
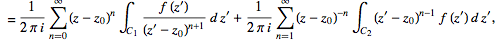 (31)
(31)
where the second term has been re-indexed. Re-indexing again,
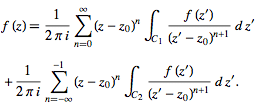 (32)
(32)
Since the integrands, including the function f(z), are analytic in the annular region defined by c1 and c2, the integrals are independent of the path of integration in that region. If we replace paths of integration c1 and c2 by a circle c of radius r with 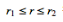 , then
, then
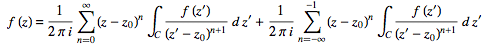 (33)
(33)
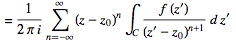 (34)
(34)
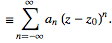 (35)
(35)
Generally, the path of integration can be any path ϒ that lies in the annular region and encircles z0 once in the positive (counterclockwise) direction.
The complex residues an are therefore defined by 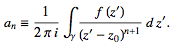 (36)
(36)
Note that the annular region itself can be expanded by increasing r1 and decreasing r2 until singularities of f(z) that lie just outside c1 or just inside c2 are reached. If f(x) has no singularities inside c2, then all the bk terms in (◇) equal zero and the Laurent series of (◇) reduces to a Taylor series with coefficients ak.
|
210 videos|156 docs|94 tests
|
FAQs on Taylor's and Laurent Series - Basic Physics for IIT JAM
| 1. What is a Taylor series? |  |
| 2. What is a Laurent series? |  |
| 3. Why are Taylor and Laurent series important in mathematics? |  |
| 4. What is the difference between a Taylor series and a Laurent series? |  |
| 5. How are Taylor and Laurent series used in the IIT JAM exam? |  |

|
Explore Courses for Physics exam
|

|

















