Work, energy and power | Basic Physics for IIT JAM PDF Download
Energy has a precise meaning in physics that does not always correspond to everyday language, and yet a precise definition is somewhat elusive. The word is derived from the Greek word ergon, meaning work, but the term work itself acquired a technical meaning with the advent of Newtonian mechanics. For example, a man pushing on a car may feel that he is doing a lot of work, but no work is actually done unless the car moves. The work done is then the product of the force applied by the man multiplied by the distance through which the car moves. If there is no friction and the surface is level, then the car, once set in motion, will continue rolling indefinitely with constant speed. The rolling car has something that a stationary car does not have—it has kinetic energy of motion equal to the work required to achieve that state of motion. The introduction of the concept of energy in this way is of great value in mechanics because, in the absence of friction, energy is never lost from the system, although it can be converted from one form to another. For example, if a coasting car comes to a hill, it will roll some distance up the hill before coming to a temporary stop. At that moment its kinetic energy of motion has been converted into its potential energy of position, which is equal to the work required to lift the car through the same vertical distance. After coming to a stop, the car will then begin rolling back down the hill until it has completely recovered its kinetic energy of motion at the bottom. In the absence of friction, such systems are said to be conservative because at any given moment the total amount of energy (kinetic plus potential) remains equal to the initial work done to set the system in motion.
As the science of physics expanded to cover an ever-wider range of phenomena, it became necessary to include additional forms of energy in order to keep the total amount of energy constant for all closed systems (or to account for changes in total energy for open systems). For example, if work is done to accelerate charged particles, then some of the resultant energy will be stored in the form of electromagnetic fields and carried away from the system as radiation. In turn the electromagnetic energy can be picked up by a remote receiver (antenna) and converted back into an equivalent amount of work. With his theory of special relativity, Albert Einstein realized that energy (E) can also be stored as mass (m) and converted back into energy, as expressed by his famous equation E = mc2, where c is the velocity of light. All of these systems are said to be conservative in the sense that energy can be freely converted from one form to another without limit. Each fundamental advance of physics into new realms has involved a similar extension to the list of the different forms of energy. In addition to preserving the first law of thermodynamics, also called the law of conservation of energy, each form of energy can be related back to an equivalent amount of work required to set the system into motion.
Thermodynamics encompasses all of these forms of energy, with the further addition of heat to the list of different kinds of energy. However, heat is fundamentally different from the others in that the conversion of work (or other forms of energy) into heat is not completely reversible, even in principle. In the example of the rolling car, some of the work done to set the car in motion is inevitably lost as heat due to friction, and the car eventually comes to a stop on a level surface. Even if all the generated heat were collected and stored in some fashion, it could never be converted entirely back into mechanical energy of motion. This fundamental limitation is expressed quantitatively by the second law of thermodynamics.
The role of friction in degrading the energy of mechanical systems may seem simple and obvious, but the quantitative connection between heat and work, as first discovered by Count Rumford, played a key role in understanding the operation of steam engines in the 19th century and similarly for all energy-conversion processes today.
Power
The quantity work has to do with a force causing a displacement. Work has nothing to do with the amount of time that this force acts to cause the displacement. Sometimes, the work is done very quickly and other times the work is done rather slowly. For example, a rock climber takes an abnormally long time to elevate her body up a few meters along the side of a cliff. On the other hand, a trail hiker (who selects the easier path up the mountain) might elevate her body a few meters in a short amount of time. The two people might do the same amount of work, yet the hiker does the work in considerably less time than the rock climber. The quantity that has to do with the rate at which a certain amount of work is done is known as the power. The hiker has a greater power rating than the rock climber.
Power is the rate at which work is done. It is the work/time ratio. Mathematically, it is computed using the following equation.
Power = Work / time
or
P = W / t
The standard metric unit of power is the Watt. As is implied by the equation for power, a unit of power is equivalent to a unit of work divided by a unit of time. Thus, a Watt is equivalent to a Joule/second. For historical reasons, the horsepower is occasionally used to describe the power delivered by a machine. One horsepower is equivalent to approximately 750 Watts.
Most machines are designed and built to do work on objects. All machines are typically described by a power rating. The power rating indicates the rate at which that machine can do work upon other objects. Thus, the power of a machine is the work/time ratio for that particular machine. A car engine is an example of a machine that is given a power rating. The power rating relates to how rapidly the car can accelerate the car. Suppose that a 40-horsepower engine could accelerate the car from 0 mi/hr to 60 mi/hr in 16 seconds. If this were the case, then a car with four times the horsepower could do the same amount of work in one-fourth the time. That is, a 160-horsepower engine could accelerate the same car from 0 mi/hr to 60 mi/hr in 4 seconds. The point is that for the same amount of work, power and time are inversely proportional. The power equation suggests that a more powerful engine can do the same amount of work in less time.
A person is also a machine that has a power rating. Some people are more power-full than others. That is, some people are capable of doing the same amount of work in less time or more work in the same amount of time. A common physics lab involves quickly climbing a flight of stairs and using mass, height and time information to determine a student's personal power. Despite the diagonal motion along the staircase, it is often assumed that the horizontal motion is constant and all the force from the steps is used to elevate the student upward at a constant speed. Thus, the weight of the student is equal to the force that does the work on the student and the height of the staircase is the upward displacement.Suppose that Ben Pumpiniron elevates his 80-kg body up the 2.0-meter stairwell in 1.8 seconds. If this were the case, then we could calculate Ben's power rating. It can be assumed that Ben must apply an 800-Newton downward force upon the stairs to elevate his body. By so doing, the stairs would push upward on Ben's body with just enough force to lift his body up the stairs. It can also be assumed that the angle between the force of the stairs on Ben and Ben's displacement is 0 degrees. With these two approximations, Ben's power rating could be determined as shown below.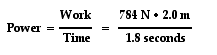
power = 871 Watts
Ben's power rating is 871 Watts. He is quite a horse.
Another Formula for Power
The expression for power is work/time. And since the expression for work is force*displacement, the expression for power can be rewritten as (force*displacement)/time. Since the expression for velocity is displacement/time, the expression for power can be rewritten once more as force*velocity. This is shown below.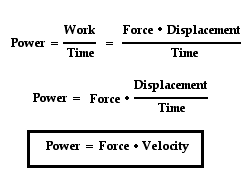
This new equation for power reveals that a powerful machine is both strong (big force) and fast (big velocity). A powerful car engine is strong and fast. A powerful piece of farm equipment is strong and fast. A powerful weightlifter is strong and fast. A powerful lineman on a football team is strong and fast. A machine that is strong enough to apply a big force to cause a displacement in a small mount of time (i.e., a big velocity) is a powerful machine.
|
210 videos|156 docs|94 tests
|
FAQs on Work, energy and power - Basic Physics for IIT JAM
| 1. What is work in the context of physics? |  |
| 2. How is energy related to work? |  |
| 3. What is the difference between kinetic energy and potential energy? |  |
| 4. How does power relate to work and energy? |  |
| 5. Can you give an example of how work, energy, and power are applied in everyday life? |  |

|
Explore Courses for Physics exam
|

|

















