Patterns in Spectra Reveal More Quantization | Modern Physics for IIT JAM PDF Download
High-resolution measurements of atomic and molecular spectra show that the spectral lines are even more complex than they first appear. In this section, we will see that this complexity has yielded important new information about electrons and their orbits in atoms.
In order to explore the substructure of atoms (and knowing that magnetic fields affect moving charges), the Dutch physicist Hendrik Lorentz (1853–1930) suggested that his student Pieter Zeeman (1865–1943) study how spectra might be affected by magnetic fields. What they found became known as the Zeeman effect, which involved spectral lines being split into two or more separate emission lines by an external magnetic field. For their discoveries, Zeeman and Lorentz shared the 1902 Nobel Prize in Physics.
Zeeman splitting is complex. Some lines split into three lines, some into five, and so on. But one general feature is that the amount the split lines are separated is proportional to the applied field strength, indicating an interaction with a moving charge. The splitting means that the quantized energy of an orbit is affected by an external magnetic field, causing the orbit to have several discrete energies instead of one. Even without an external magnetic field, very precise measurements showed that spectral lines are doublets (split into two), apparently by magnetic fields within the atom itself.
The Zeeman effect is the splitting of spectral lines when a magnetic field is applied. The number of lines formed varies, but the spread is proportional to the strength of the applied field.
(a) Two spectral lines with no external magnetic field.
(b) The lines split when the field is applied.
(c) The splitting is greater when a stronger field is applied.

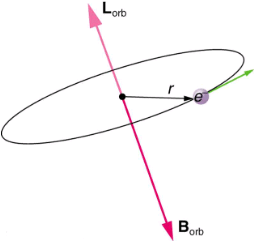
Bohr’s theory of circular orbits is useful for visualizing how an electron’s orbit is affected by a magnetic field. The circular orbit forms a current loop, which creates a magnetic field of its own, Borb as seen in. Note that the orbital magnetic field Borb and the orbital angular momentum Lorb are along the same line. The external magnetic field and the orbital magnetic field interact; a torque is exerted to align them. A torque rotating a system through some angle does work so that there is energy associated with this interaction. Thus, orbits at different angles to the external magnetic field have different energies. What is remarkable is that the energies are quantized—the magnetic field splits the spectral lines into several discrete lines that have different energies. This means that only certain angles are allowed between the orbital angular momentum and the external field, as seen in.
The approximate picture of an electron in a circular orbit illustrates how the current loop produces its own magnetic field, called Borb. It also shows how Borb is along the same line as the orbital angular momentum Lorb.
Only certain angles are allowed between the orbital angular momentum and an external magnetic field. This is implied by the fact that the Zeeman effect splits spectral lines into several discrete lines. Each line is associated with an angle between the external magnetic field and magnetic fields due to electrons and their orbits.
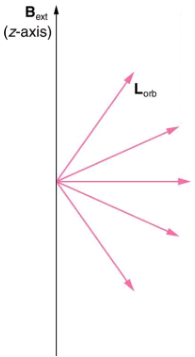
We already know that the magnitude of angular momentum is quantized for electron orbits in atoms. The new insight is that the direction of the orbital angular momentum is also quantized. The fact that the orbital angular momentum can have only certain directions is called space quantization. Like many aspects of quantum mechanics, this quantization of direction is totally unexpected. On the macroscopic scale, orbital angular momentum, such as that of the moon around the earth, can have any magnitude and be in any direction.
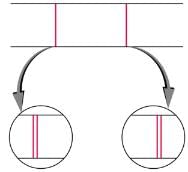
Detailed treatment of space quantization began to explain some complexities of atomic spectra, but certain patterns seemed to be caused by something else. As mentioned, spectral lines are actually closely spaced doublets, a characteristic called fine structure. The doublet changes when a magnetic field is applied, implying that whatever causes the doublet interacts with a magnetic field. In 1925, Sem Goudsmit and George Uhlenbeck, two Dutch physicists, successfully argued that electrons have properties analogous to a macroscopic charge spinning on its axis. Electrons, in fact, have an internal or intrinsic angular momentum called intrinsic spin S. Since electrons are charged, their intrinsic spin creates an intrinsic magnetic field Bint, which interacts with their orbital magnetic field Borb. Furthermore, electron intrinsic spin is quantized in magnitude and direction, analogous to the situation for orbital angular momentum. The spin of the electron can have only one magnitude, and its direction can be at only one of two angles relative to a magnetic field, as seen in. We refer to this as spin up or spin down for the electron. Each spin direction has a different energy; hence, spectroscopic lines are split into two. Spectral doublets are now understood as being due to electron spin.
Fine structure. Upon close examination, spectral lines are doublets, even in the absence of an external magnetic field. The electron has an intrinsic magnetic field that interacts with its orbital magnetic field.
The intrinsic magnetic field Bint of an electron is attributed to its spin, S, roughly pictured to be due to its charge spinning on its axis. This is only a crude model, since electrons seem to have no size. The spin and intrinsic magnetic field of the electron can make only one of two angles with another magnetic field, such as that created by the electron’s orbital motion. Space is quantized for spin as well as for orbital angular momentum.
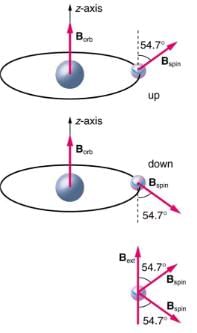
These two new insights—that the direction of angular momentum, whether orbital or spin, is quantized, and that electrons have intrinsic spin—help to explain many of the complexities of atomic and molecular spectra. In magnetic resonance imaging, it is the way that the intrinsic magnetic field of hydrogen and biological atoms interact with an external field that underlies the diagnostic fundamentals.
Section Summary:
- The Zeeman effect—the splitting of lines when a magnetic field is applied—is caused by other quantized entities in atoms.
- Both the magnitude and direction of orbital angular momentum are quantized.
- The same is true for the magnitude and direction of the intrinsic spin of electrons.
|
52 videos|44 docs|15 tests
|
FAQs on Patterns in Spectra Reveal More Quantization - Modern Physics for IIT JAM
| 1. What are patterns in spectra? |  |
| 2. How do patterns in spectra reveal quantization? |  |
| 3. What information can be obtained from analyzing spectra patterns? |  |
| 4. How can quantization be observed in a spectrum? |  |
| 5. What are the applications of studying patterns in spectra? |  |

|
Explore Courses for Physics exam
|

|

















