Kinetic Theory: Atomic and Molecular Explanation of Pressure and Temperature | Basic Physics for IIT JAM PDF Download
We have developed macroscopic definitions of pressure and temperature. Pressure is the force divided by the area on which the force is exerted, and temperature is measured with a thermometer. We gain a better understanding of pressure and temperature from the kinetic theory of gases, which assumes that atoms and molecules are in continuous random motion.
When a molecule collides with a rigid wall, the component of its momentum perpendicular to the wall is reversed. A force is thus exerted on the wall, creating pressure.
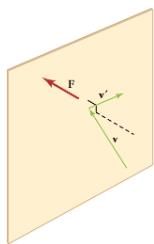
It shows an elastic collision of a gas molecule with the wall of a container, so that it exerts a force on the wall (by Newton’s third law). Because a huge number of molecules will collide with the wall in a short time, we observe an average force per unit area. These collisions are the source of pressure in a gas. As the number of molecules increases, the number of collisions and thus the pressure increase. Similarly, the gas pressure is higher if the average velocity of molecules is higher. The actual relationship is derived in the Things Great and Small feature below. The following relationship is found: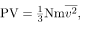
where P is the pressure (average force per unit area), V is the volume of gas in the container, N is the number of molecules in the container, m is the mass of a molecule, and 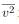 is the average of the molecular speed squared.
is the average of the molecular speed squared.
What can we learn from this atomic and molecular version of the ideal gas law? We can derive a relationship between temperature and the average translational kinetic energy of molecules in a gas. Recall the previous expression of the ideal gas law:
PV = NkT
Equating the right-hand side of this equation with the right-hand side of PV = 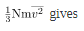
Making Connections: Things Great and Small—Atomic and Molecular Origin of Pressure in a Gas.
shows a box filled with a gas. We know from our previous discussions that putting more gas into the box produces greater pressure, and that increasing the temperature of the gas also produces a greater pressure. But why should increasing the temperature of the gas increase the pressure in the box? A look at the atomic and molecular scale gives us some answers, and an alternative expression for the ideal gas law.
The figure shows an expanded view of an elastic collision of a gas molecule with the wall of a container. Calculating the average force exerted by such molecules will lead us to the ideal gas law, and to the connection between temperature and molecular kinetic energy. We assume that a molecule is small compared with the separation of molecules in the gas, and that its interaction with other molecules can be ignored. We also assume the wall is rigid and that the molecule’s direction changes, but that its speed remains constant (and hence its kinetic energy and the magnitude of its momentum remain constant as well). This assumption is not always valid, but the same result is obtained with a more detailed description of the molecule’s exchange of energy and momentum with the wall.
Gas in a box exerts an outward pressure on its walls. A molecule colliding with a rigid wall has the direction of its velocity and momentum in the x-direction reversed. This direction is perpendicular to the wall. The components of its velocity momentum in the y– and z-directions are not changed, which means there is no force parallel to the wall.
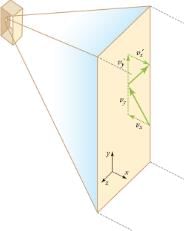
If the molecule’s velocity changes in the x-direction, its momentum changes from -mvx to +mvx. Thus, its change in momentum is mv = +mvx -(-mvx) = 2mvx. The force exerted on the molecule is given by
F = p/t = 2mvx/t
There is no force between the wall and the molecule until the molecule hits the wall. During the short time of the collision, the force between the molecule and wall is relatively large. We are looking for an average force; we take t to be the average time between collisions of the molecule with this wall. It is the time it would take the molecule to go across the box and back (a distance 2l right) at a speed of vx. Thus t = 2l/vx, and the expression for the force becomes
This force is due to one molecule. We multiply by the number of molecules N and use their average squared velocity to find the force
where the bar over a quantity means its average value. We would like to have the force in terms of the speed v, rather than the x-component of the velocity. We note that the total velocity squared is the sum of the squares of its components, so that
Because the velocities are random, their average components in all directions are the same:
Thus,
or
Substituting into the expression for F gives
The pressure is F/A, so that we obtain
where we used V=Al for the volume. This gives the important result.
This equation is another expression of the ideal gas law.
We can get the average kinetic energy of a molecule, 1/2mv2, from the left-hand side of the equation by canceling N and multiplying by 3/2. This calculation produces the result that the average kinetic energy of a molecule is directly related to absolute temperature.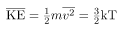
The average translational kinetic energy of a molecule,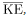 is called thermal energy. The equation
is called thermal energy. The equation 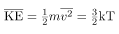 is a molecular interpretation of temperature, and it has been found to be valid for gases and reasonably accurate in liquids and solids. It is another definition of temperature based on an expression of the molecular energy.
is a molecular interpretation of temperature, and it has been found to be valid for gases and reasonably accurate in liquids and solids. It is another definition of temperature based on an expression of the molecular energy.
It is sometimes useful to rearrange 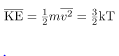 , and solve for the average speed of molecules in a gas in terms of temperature,
, and solve for the average speed of molecules in a gas in terms of temperature,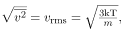
where vrms stands for root-mean-square (rms) speed.
Distribution of Molecular Speeds
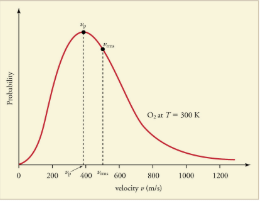
The motion of molecules in a gas is random in magnitude and direction for individual molecules, but a gas of many molecules has a predictable distribution of molecular speeds. This distribution is called the Maxwell-Boltzmann distribution, after its originators, who calculated it based on kinetic theory, and has since been confirmed experimentally.The distribution has a long tail, because a few molecules may go several times the rms speed. The most probable speed  is less than the rms speed vrms. shows that the curve is shifted to higher speeds at higher temperatures, with a broader range of speeds.
is less than the rms speed vrms. shows that the curve is shifted to higher speeds at higher temperatures, with a broader range of speeds.
The Maxwell-Boltzmann distribution of molecular speeds in an ideal gas. The most likely speed vp is less than the rms speed vrms. Although very high speeds are possible, only a tiny fraction of the molecules have speeds that are an order of magnitude greater than vrms.
The distribution of thermal speeds depends strongly on temperature. As temperature increases, the speeds are shifted to higher values and the distribution is broadened.
The Maxwell-Boltzmann distribution is shifted to higher speeds and is broadened at higher temperatures.
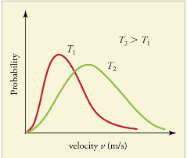
What is the implication of the change in distribution with temperature shown in [link] for humans? All other things being equal, if a person has a fever, he or she is likely to lose more water molecules, particularly from linings along moist cavities such as the lungs and mouth, creating a dry sensation in the mouth.
This photograph of Apollo 17 Commander Eugene Cernan driving the lunar rover on the Moon in 1972 looks as though it was taken at night with a large spotlight. In fact, the light is coming from the Sun. Because the acceleration due to gravity on the Moon is so low (about 1/6 that of Earth), the Moon’s escape velocity is much smaller. As a result, gas molecules escape very easily from the Moon, leaving it with virtually no atmosphere. Even during the daytime, the sky is black because there is no gas to scatter sunlight.

Check Your Understanding
If you consider a very small object such as a grain of pollen, in a gas, then the number of atoms and molecules striking its surface would also be relatively small. Would the grain of pollen experience any fluctuations in pressure due to statistical fluctuations in the number of gas atoms and molecules striking it in a given amount of time?
Yes. Such fluctuations actually occur for a body of any size in a gas, but since the numbers of atoms and molecules are immense for macroscopic bodies, the fluctuations are a tiny percentage of the number of collisions, and the averages spoken of in this section vary imperceptibly. Roughly speaking the fluctuations are proportional to the inverse square root of the number of collisions, so for small bodies they can become significant. This was actually observed in the 19th century for pollen grains in water, and is known as the Brownian effect.
Section Summary
- Kinetic theory is the atomistic description of gases as well as liquids and solids.
- Kinetic theory models the properties of matter in terms of continuous random motion of atoms and molecules.
- The ideal gas law can also be expressed as
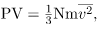 where P is the pressure (average force per unit area), V is the volume of gas in the container, N is the number of molecules in the container, m is the mass of a molecule, and
where P is the pressure (average force per unit area), V is the volume of gas in the container, N is the number of molecules in the container, m is the mass of a molecule, and 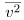 is the average of the molecular speed squared.
is the average of the molecular speed squared. - Thermal energy is defined to be the average translational kinetic energy
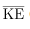 of an atom or molecule.
of an atom or molecule. - The temperature of gases is proportional to the average translational kinetic energy of atoms and molecules.
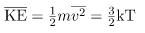 or
or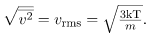
- The motion of individual molecules in a gas is random in magnitude and direction. However, a gas of many molecules has a predictable distribution of molecular speeds, known as the Maxwell-Boltzmann distribution.
|
217 videos|156 docs|94 tests
|
















