Complex Number With Examples | Algebra - Mathematics PDF Download
Complex Numbers
In the radicals section we noted that we won’t get a real number out of a square root of a negative number. For instance, √-9 isn’t a real number since there is no real number that we can square and get a NEGATIVE 9.
Now we also saw that if aa and bb were both positive then√ab = √a√b For a second let’s forget that restriction and do the following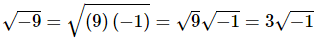
Now, √-1 is not a real number, but if you think about it we can do this for any square root of a negative number. For instance,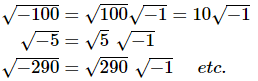
So, even if the number isn’t a perfect square we can still always reduce the square root of a negative number down to the square root of a positive number (which we or a calculator can deal with) times √-1.So, if we just had a way to deal with √-1 we could actually deal with square roots of negative numbers. Well the reality is that, at this level, there just isn’t any way to deal with √-1 so instead of dealing with it we will “make it go away” so to speak by using the following definition.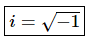
Note that if we square both sides of this we get,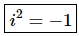
It will be important to remember this later on. This shows that, in some way, ii is the only “number” that we can square and get a negative value.Using this definition all the square roots above become,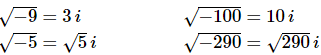
these are all examples of complex numbers.The natural question at this point is probably just why do we care about this? The answer is that, as we will see in the next chapter, sometimes we will run across the square roots of negative numbers and we’re going to need a way to deal with them. So, to deal with them we will need to discuss complex numbers.So, let’s start out with some of the basic definitions and terminology for complex numbers. The standard form of a complex number is
a + bi
Where a and b are real numbers and they can be anything, positive, negative, zero, integers, fractions, decimals, it doesn’t matter. When in the standard form aa is called the real part of the complex number and bb is called the imaginary part of the complex number.
Here are some examples of complex numbers.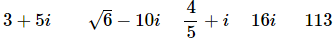
The last two probably need a little more explanation. It is completely possible that aa or bb could be zero and so in 16i the real part is zero. When the real part is zero we often will call the complex number a purely imaginary number. In the last example (113) the imaginary part is zero and we actually have a real number. So, thinking of numbers in this light we can see that the real numbers are simply a subset of the complex numbers.
The conjugate of the complex number a+bi is the complex number a−bi. In other words, it is the original complex number with the sign on the imaginary part changed. Here are some examples of complex numbers and their conjugates.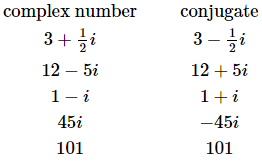
Notice that the conjugate of a real number is just itself with no changes.
Now we need to discuss the basic operations for complex numbers. We’ll start with addition and subtraction. The easiest way to think of adding and/or subtracting complex numbers is to think of each complex number as a polynomial and do the addition and subtraction in the same way that we add or subtract polynomials.
Example 1: Perform the indicated operation and write the answers in standard form.
(a) (−4+7i)+(5−10i)
(b) 4+12i)−(3−15i)
(c) 5i−(−9+i)
Solution: There really isn’t much to do here other than add or subtract. Note that the parentheses on the first terms are only there to indicate that we’re thinking of that term as a complex number and in general aren’t used.
(a) (−4+7i)+(5−10i)=1−3i
(b) (4+12i)−(3−15i)=4+12i−3+15i=1+27i
(c) 5i−(−9+i)=5i+9−i=9+4i
Next let’s take a look at multiplication. Again, with one small difference, it’s probably easiest to just think of the complex numbers as polynomials so multiply them out as you would polynomials. The one difference will come in the final step as we’ll see.
Example 2: Multiply each of the following and write the answers in standard form.
(a) 7i(−5+2i)
(b) (1−5i)(−9+2i)
(c) (4+i)(2+3i)
(d) (1−8i)(1+8i)
Solution: (a) (−4+7i)+(5−10i)=1−3i
So all that we need to do is distribute the 7i through the parenthesis.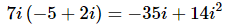
Now, this is where the small difference mentioned earlier comes into play. This number is NOT in standard form. The standard form for complex numbers does not have an i2 in it. This however is not a problem provided we recall that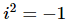
Using this we get,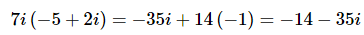
We also rearranged the order so that the real part is listed first.
(b) (1−5i)(−9+2i)
In this case we will FOIL the two numbers and we’ll need to also remember to get rid of the i2.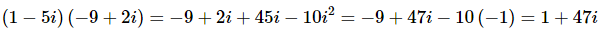
(c) (4+i)(2+3i)
Same thing with this one.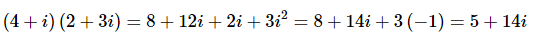
(d) (1−8i)(1+8i)
Here’s one final multiplication that will lead us into the next topic.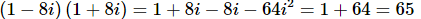
Don’t get excited about it when the product of two complex numbers is a real number. That can and will happen on occasion.
In the final part of the previous example we multiplied a number by its conjugate. There is a nice general formula for this that will be convenient when it comes to discussing division of complex numbers.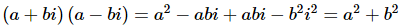
So, when we multiply a complex number by its conjugate we get a real number given by,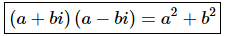
Now, we gave this formula with the comment that it will be convenient when it came to dividing complex numbers so let’s look at a couple of examples.
Example 3: Write each of the following in standard form.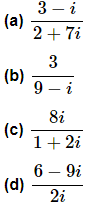
Solution: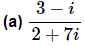
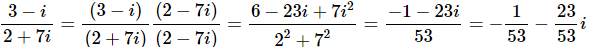
Notice that to officially put the answer in standard form we broke up the fraction into the real and imaginary parts.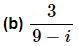
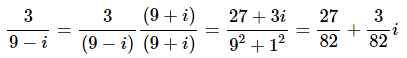
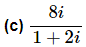
This one is a little different from the previous ones since the denominator is a pure imaginary number. It can be done in the same manner as the previous ones, but there is a slightly easier way to do the problem.
First, break up the fraction as follows.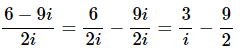
Now, we want the i out of the denominator and since there is only an i in the denominator of the first term we will simply multiply the numerator and denominator of the first term by an i.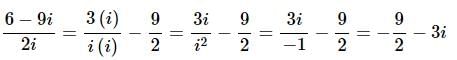
The next topic that we want to discuss here is powers of i. Let’s just take a look at what happens when we start looking at various powers of i.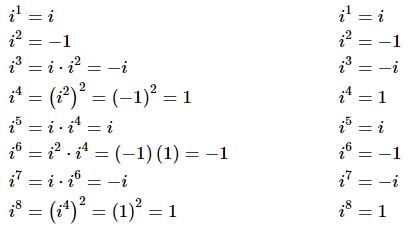
Can you see the pattern? All powers if i can be reduced down to one of four possible answers and they repeat every four powers. This can be a convenient fact to remember.
We next need to address an issue on dealing with square roots of negative numbers. From the section on radicals we know that we can do the following.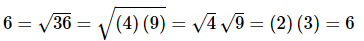
In other words, we can break up products under a square root into a product of square roots provided both numbers are positive.
It turns out that we can actually do the same thing if one of the numbers is negative. For instance,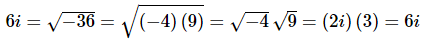
However, if BOTH numbers are negative this won’t work anymore as the following shows.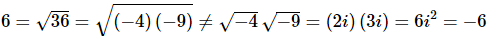
We can summarize this up as a set of rules. If a and b are both positive numbers then,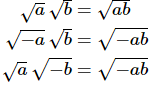
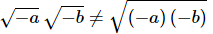
Why is this important enough to worry about? Consider the following example.
Example 4: Multiply the following and write the answer in standard form.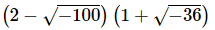
Solution:
The rule of thumb given in the previous example is important enough to make again. When faced with square roots of negative numbers the first thing that you should do is convert them to complex numbers.
There is one final topic that we need to touch on before leaving this section. As we noted back in the section on radicals even though √9 = 3 there are in fact two numbers that we can square to get 9. We can square both 3 and -3.
The same will hold for square roots of negative numbers. As we saw earlier √9 = 3i.
As with square roots of positive numbers in this case we are really asking what did we square to get -9? Well it’s easy enough to check that 3i is correct.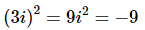
However, that is not the only possibility. Consider the following,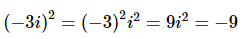
and so if we square -3i we will also get -9. So, when taking the square root of a negative number there are really two numbers that we can square to get the number under the radical. However, we will ALWAYS take the positive number for the value of the square root just as we do with the square root of positive numbers.
|
181 videos|58 docs
|
FAQs on Complex Number With Examples - Algebra - Mathematics
| 1. What are complex numbers? |  |
| 2. How do complex numbers differ from real numbers? |  |
| 3. What is the significance of the imaginary unit (i) in complex numbers? |  |
| 4. Can complex numbers be represented graphically? |  |
| 5. How are complex numbers used in practical applications? |  |
















