Problems for practice | Algebra - Mathematics PDF Download
1. For problems 1 – 3 perform an index shift so that the series starts at n=3.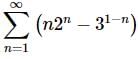
Solution. There really isn’t all that much to this problem. Just remember that, in this case, we’ll need to increase the initial value of the index by two so it will start at n=3 and this means all the n’s in the series terms will need to decrease by the same amount (two in this case…).
Doing this gives the following series.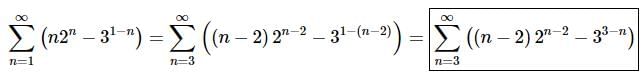
Be careful with parenthesis, exponents, coefficients and negative signs when “shifting” the n’s in the series terms. When replacing n with n−2 make sure to add in parenthesis where needed to preserve coefficients and minus signs.
2. Perform an index shift so that the following series starts at n = 3 .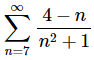
Solution. There really isn’t all that much to this problem. Just remember that, in this case, we’ll need to decrease the initial value of the index by four so it will start at n=3 and this means all the n’s in the series terms will need to increase by the same amount (four in this case…).
Doing this gives the following series.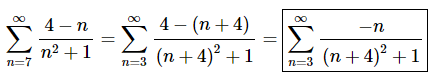
Be careful with parenthesis, exponents, coefficients and negative signs when “shifting” the n’s in the series terms. When replacing n with n+4 make sure to add in parenthesis where needed to preserve coefficients and minus signs.
3. Perform an index shift so that the following series starts at n = 3 .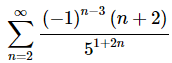
Solution. There really isn’t all that much to this problem. Just remember that, in this case, we’ll need to increase the initial value of the index by one so it will start at n=3 and this means all the n’s in the series terms will need to decrease by the same amount (one in this case…).
Doing this gives the following series.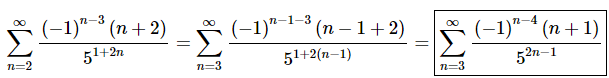
Be careful with parenthesis, exponents, coefficients and negative signs when “shifting” the n’s in the series terms. When replacing n with n−1 make sure to add in parenthesis where needed to preserve coefficients and minus signs.
4. Strip out the first 3 terms from the series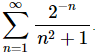
Solution. Remember that when we say we are going to “strip out” terms from a series we aren’t really getting rid of them. All we are doing is writing the first few terms of the series as a summation in front of the series.
So, for this series stripping out the first three terms gives,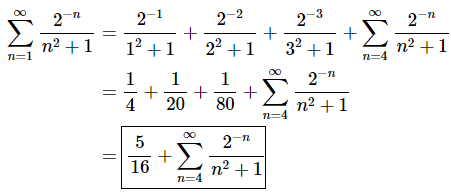
This first step isn’t really all that necessary but was included here to make it clear that we were plugging in n=1, n=2 and n=3 (i.e. the first three values of n) into the general series term. Also, don’t forget to change the starting value of n to reflect the fact that we’ve “stripped out” the first three values of n or terms.
5. Given that 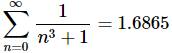 determine the value of
determine the value of 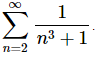
Solution. First notice that if we strip out the first two terms from the series that starts at n=0 the result will involve a series that starts at n=2.
Doing this gives,
Now, for this situation we are given the value of the series that starts at n=0 and are asked to determine the value of the series that starts at n=2. To do this all we need to do is plug in the known value of the series that starts at n=0 into the “equation” above and “solve” for the value of the series that starts at n=2.
This gives,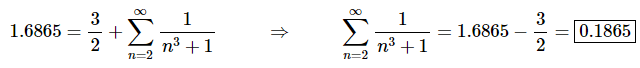
For problems 6 & 7 compute the first 3 terms in the sequence of partial sums for the given series.
6. 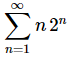
Solution. Remember that nth term in the sequence of partial sums is just the sum of the first n terms of the series. So, computing the first three terms in the sequence of partial sums is pretty simple to do.
Here is the work for this problem.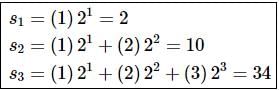
7. 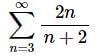
Solution. Remember that nth term in the sequence of partial sums is just the sum of the first n terms of the series. So, computing the first three terms in the sequence of partial sums is pretty simple to do.
Here is the work for this problem.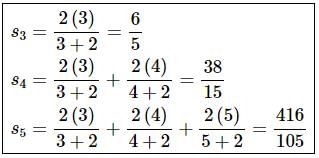
For problems 8 & 9 assume that the nth term in the sequence of partial sums for the series 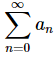 is given below. Determine if the series
is given below. Determine if the series 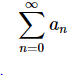 is convergent or divergent. If the series is convergent determine the value of the series.
is convergent or divergent. If the series is convergent determine the value of the series.
8. 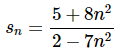
Solution. There really isn’t all that much that we need to do here other than to recall,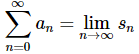
So, to determine if the series converges or diverges, all we need to do is compute the limit of the sequence of the partial sums. The limit of the sequence of partial sums is,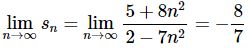
Now, we can see that this limit exists and is finite (i.e. is not plus/minus infinity). Therefore, we now know that the series,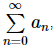 converges and its value is,
converges and its value is,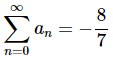
If you are unfamiliar with limits at infinity then you really need to go back to the Calculus I material and do some review of limits at infinity and L’Hospital’s Rule as we will be doing quite a bit of these kinds of limits off and on over the next few sections.
9. 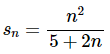
Solution. There really isn’t all that much that we need to do here other than to recall,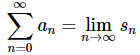
So, to determine if the series converges or diverges, all we need to do is compute the limit of the sequence of the partial sums. The limit of the sequence of partial sums is,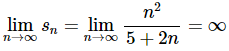
Now, we can see that this limit exists and is infinite. Therefore, we now know that the series,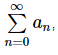 diverges.
diverges.
If you are unfamiliar with limits at infinity then you really need to go back to the Calculus I material and do some review of limits at infinity and L’Hospital’s Rule as we will be doing quite a bit of these kinds of limits off and on over the next few sections.
For problems 10 & 11 show that the series is divergent.
10. 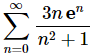
Solution. First let’s note that we’re being asked to show that the series is divergent. We are not being asked to determine if the series is divergent. At this point we really only know of two ways to actually show this.
The first option is to show that the limit of the sequence of partial sums either doesn’t exist or is infinite. The problem with this approach is that for many series determining the general formula for the nth term of the sequence of partial sums is very difficult if not outright impossible to do. That is true for this series and so that is not really a viable option for this problem.
Luckily enough for us there is actually an easier option to simply show that a series is divergent. All we need to do is use the Divergence Test.
The limit of the series terms is,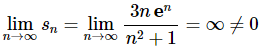
The limit of the series terms is not zero and so by the Divergence Test we know that the series in this problem is divergence.
11. 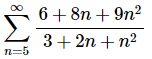
Solution. First let’s note that we’re being asked to show that the series is divergent. We are not being asked to determine if the series is divergent. At this point we really only know of two ways to actually show this.
The first option is to show that the limit of the sequence of partial sums either doesn’t exist or is infinite. The problem with this approach is that for many series determining the general formula for the nth term of the sequence of partial sums is very difficult if not outright impossible to do. That is true for this series and so that is not really a viable option for this problem.
Luckily enough for us there is actually an easier option to simply show that a series is divergent. All we need to do is use the Divergence Test.
The limit of the series terms is,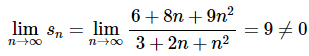
The limit of the series terms is not zero and so by the Divergence Test we know that the series in this problem is divergence.
|
161 videos|58 docs
|
FAQs on Problems for practice - Algebra - Mathematics
| 1. What are the different types of angles in mathematics? |  |
| 2. How do you find the area of a triangle? |  |
| 3. What is the Pythagorean theorem? |  |
| 4. How do you solve linear equations? |  |
| 5. What is the difference between mean, median, and mode in statistics? |  |

|
Explore Courses for Mathematics exam
|

|

















