Computing Indefinite Integrals | Calculus - Mathematics PDF Download
Computing Indefinite Integral
In the previous section we started looking at indefinite integrals and in that section we concentrated almost exclusively on notation, concepts and properties of the indefinite integral. In this section we need to start thinking about how we actually compute indefinite integrals. We’ll start off with some of the basic indefinite integrals.
The first integral that we’ll look at is the integral of a power of x.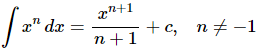
The general rule when integrating a power of xx we add one onto the exponent and then divide by the new exponent. It is clear (hopefully) that we will need to avoid n=−1 in this formula. If we allow n=−1 in this formula we will end up with division by zero. We will take care of this case in a bit.
Next is one of the easier integrals but always seems to cause problems for people.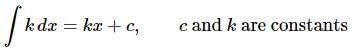
If you remember that all we’re asking is what did we differentiate to get the integrand this is pretty simple, but it does seem to cause problems on occasion.
Let’s now take a look at the trig functions.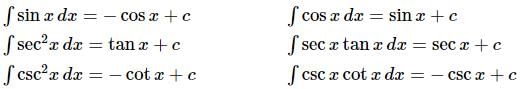
Notice that we only integrated two of the six trig functions here. The remaining four integrals are really integrals that give the remaining four trig functions. Also, be careful with signs here. It is easy to get the signs for derivatives and integrals mixed up. Again, remember that we’re asking what function we differentiated to get the integrand.
We will be able to integrate the remaining four trig functions in a couple of sections, but they all require the Substitution Rule.
Now, let’s take care of exponential and logarithm functions.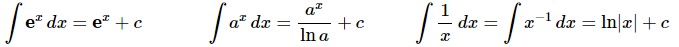
Integrating logarithms requires a topic that is usually taught in Calculus II and so we won’t be integrating a logarithm in this class. Also note the third integrand can be written in a couple of ways and don’t forget the absolute value bars in the xx in the answer to the third integral.
Finally, let’s take care of the inverse trig and hyperbolic functions.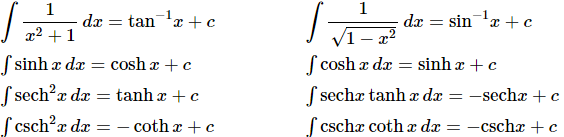
As with logarithms integrating inverse trig functions requires a topic usually taught in Calculus II and so we won’t be integrating them in this class. There is also a different answer for the second integral above. Recalling that since all we are asking here is what function did we differentiate to get the integrand the second integral could also be,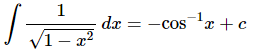
Traditionally we use the first form of this integral.
Okay, now that we’ve got most of the basic integrals out of the way let’s do some indefinite integrals. In all of these problems remember that we can always check our answer by differentiating and making sure that we get the integrand.
Example 1: Evaluate each of the following indefinite integrals.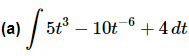
Ans: There’s not really a whole lot to do here other than use the first two formulas from the beginning of this section. Remember that when integrating powers (that aren’t -1 of course) we just add one onto the exponent and then divide by the new exponent.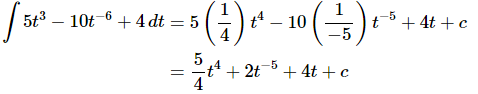
Be careful when integrating negative exponents. Remember to add one onto the exponent. One of the more common mistakes that students make when integrating negative exponents is to “add one” and end up with an exponent of “-7” instead of the correct exponent of “-5”.
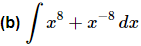
Ans: This is here just to make sure we get the point about integrating negative exponents.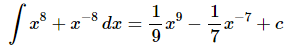
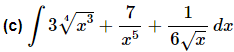
Ans: In this case there isn’t a formula for explicitly dealing with radicals or rational expressions. However, just like with derivatives we can write all these terms so they are in the numerator and they all have an exponent. This should always be your first step when faced with this kind of integral just as it was when differentiating.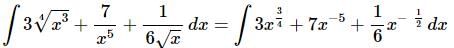
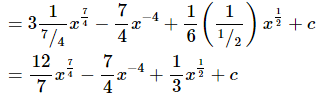
When dealing with fractional exponents we usually don’t “divide by the new exponent”. Doing this is equivalent to multiplying by the reciprocal of the new exponent and so that is what we will usually do.
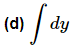
Ans. Don’t make this one harder than it is…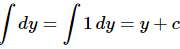
In this case we are really just integrating a one!
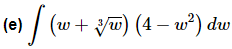
Ans. We’ve got a product here and as we noted in the previous section there is no rule for dealing with products. However, in this case we don’t need a rule. All that we need to do is multiply things out (taking care of the radicals at the same time of course) and then we will be able to integrate.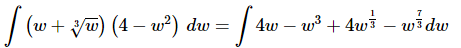
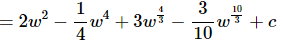
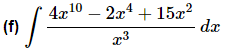
Ans. As with the previous part it’s not really a problem that we don’t have a rule for quotients for this integral. In this case all we need to do is break up the quotient and then integrate the individual terms.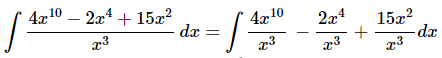
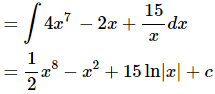
Be careful to not think of the third term as x to a power for the purposes of integration. Using that rule on the third term will NOT work. The third term is simply a logarithm. Also, don’t get excited about the 15. The 15 is just a constant and so it can be factored out of the integral. In other words, here is what we did to integrate the third term.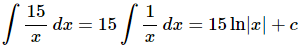
Always remember that you can’t integrate products and quotients in the same way that we integrate sums and differences. At this point the only way to integrate products and quotients is to multiply the product out or break up the quotient. Eventually we’ll see some other products and quotients that can be dealt with in other ways. However, there will never be a single rule that will work for all products and there will never be a single rule that will work for all quotients. Every product and quotient is different and will need to be worked on a case by case basis.
The first set of examples focused almost exclusively on powers of x (or whatever variable we used in each example). It’s time to do some examples that involve other functions.
Example 2: Evaluate each of the following integrals.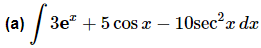
Ans. There isn’t anything to this one other than using the formulas.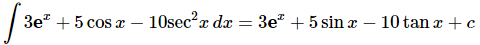

Ans. Let’s be a little careful with this one. First break it up into two integrals and note the rewritten integrand on the second integral.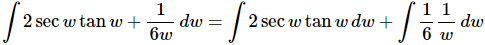
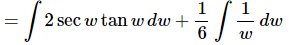
Rewriting the second integrand will help a little with the integration at this early stage. We can think of the 6 in the denominator as a 1/6 out in front of the term and then since this is a constant it can be factored out of the integral. The answer is then,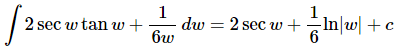
Note that we didn’t factor the 2 out of the first integral as we factored the 1/6 out of the second. In fact, we will generally not factor the 1/6 out either in later problems. It was only done here to make sure that you could follow what we were doing.
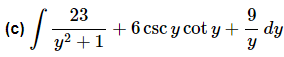
Ans. In this one we’ll just use the formulas from above and don’t get excited about the coefficients. They are just multiplicative constants and so can be ignored while we integrate each term and then once we’re done integrating a given term we simply put the coefficients back in.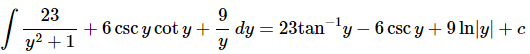
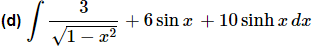
Ans. Again, there really isn’t a whole lot to do with this one other than to use the appropriate formula from above while taking care of coefficients.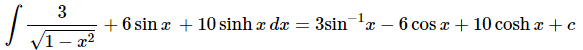
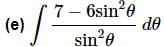
Ans. This one can be a little tricky if you aren’t ready for it. As discussed previously, at this point the only way we have of dealing with quotients is to break it up.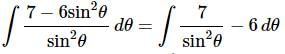
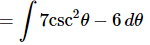
Notice that upon breaking the integral up we further simplified the integrand by recalling the definition of cosecant. With this simplification we can do the integral.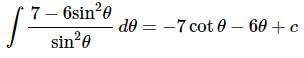
As shown in the last part of this example we can do some fairly complicated looking quotients at this point if we remember to do simplifications when we see them. In fact, this is something that you should always keep in mind. In almost any problem that we’re doing here don’t forget to simplify where possible. In almost every case this can only help the problem and will rarely complicate the problem.
In the next problem we’re going to take a look at a product and this time we’re not going to be able to just multiply the product out. However, if we recall the comment about simplifying a little this problem becomes fairly simple.
Example 3: Integrate 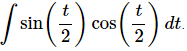
Ans. There are several ways to do this integral and most of them require the next section. However, there is a way to do this integral using only the material from this section. All that is required is to remember the trig formula that we can use to simplify the integrand up a little. Recall the following double angle formula.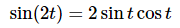
A small rewrite of this formula gives,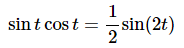
If we now replace all the t’s with t/2 we get,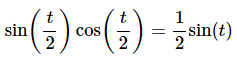
Using this formula, the integral becomes something we can do.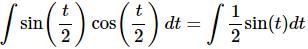
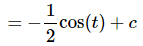
As noted earlier there is another method for doing this integral. In fact, there are two alternate methods. To see all three check out the section on Constant of Integration in the Extras chapter but be aware that the other two do require the material covered in the next section.
The formula/simplification in the previous problem is a nice “trick” to remember. It can be used on occasion to greatly simplify some problems.
There is one more set of examples that we should do before moving out of this section.
Example: 4 Given the following information determine the function f(x).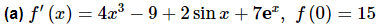
Ans. The first step here is integrating to determine the most general possible f(x).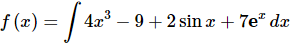
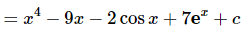
Now we have a value of the function so let’s plug in x=0 and determine the value of the constant of integration c.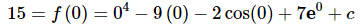
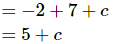
So, from this it looks like c=10. This means that the function is,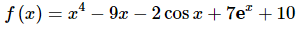
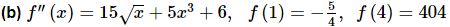
Ans. This one is a little different form the first one. In order to get the function we will need the first derivative and we have the second derivative. We can however, use an integral to get the first derivative from the second derivative, just as we used an integral to get the function from the first derivative.
So, let’s first get the most general possible first derivative by integrating the second derivative.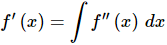
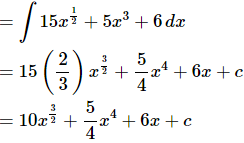
Don’t forget the constant of integration!
We can now find the most general possible function by integrating the first derivative which we found above.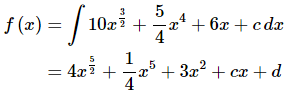
Do not get excited about integrating the cc. It’s just a constant and we know how to integrate constants. Also, there will be no reason to think the constants of integration from the integration in each step will be the same and so we’ll need to call each constant of integration something different, dd in this case.
Now, plug in the two values of the function that we’ve got.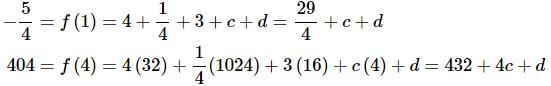
This gives us a system of two equations in two unknowns that we can solve.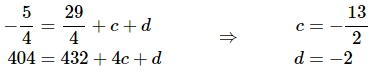
The function is then,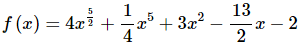
Don’t remember how to solve systems? Check out the Solving Systems portion of the Algebra/Trig Review.
In this section we’ve started the process of integration. We’ve seen how to do quite a few basic integrals and we also saw a quick application of integrals in the last example.
There are many new formulas in this section that we’ll now have to know. However, if you think about it, they aren’t really new formulas. They are really nothing more than derivative formulas that we should already know written in terms of integrals. If you remember that you should find it easier to remember the formulas in this section.
Always remember that integration is asking nothing more than what function did we differentiate to get the integrand. If you can remember that many of the basic integrals that we saw in this section and many of the integrals in the coming sections aren’t too bad.
Practice problems: Computing Indefinite Integrals
Q.1. Evaluate 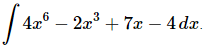
Ans. There really isn’t too much to do other than to evaluate the integral.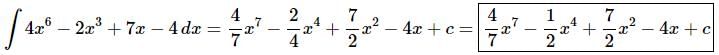
Don’t forget to add on the “+c” since we know that we are asking what function did we differentiate to get the integrand and the derivative of a constant is zero and so we do need to add that onto the answer.
Q.2. Evaluate 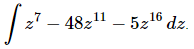
Ans. There really isn’t too much to do other than to evaluate the integral.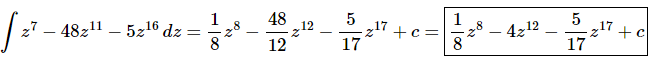
Don’t forget to add on the “+c” since we know that we are asking what function did we differentiate to get the integrand and the derivative of a constant is zero and so we do need to add that onto the answer.
Q.3. Evaluate 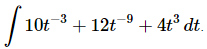
Ans. There really isn’t too much to do other than to evaluate the integral.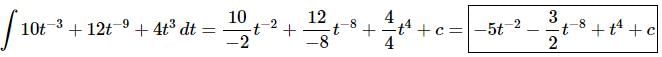
Don’t forget to add on the “+c” since we know that we are asking what function did we differentiate to get the integrand and the derivative of a constant is zero and so we do need to add that onto the answer.
Q.4. Evaluate 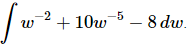
Ans. There really isn’t too much to do other than to evaluate the integral.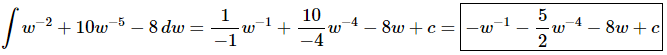
Don’t forget to add on the “+c” since we know that we are asking what function did we differentiate to get the integrand and the derivative of a constant is zero and so we do need to add that onto the answer.
Q.5. Evaluate 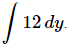
Ans. There really isn’t too much to do other than to evaluate the integral.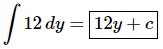
Don’t forget to add on the “+c” since we know that we are asking what function did we differentiate to get the integrand and the derivative of a constant is zero and so we do need to add that onto the answer.
Q.6. Evaluate 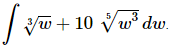
Ans. We first need to convert the roots to fractional exponents.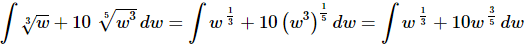
Once we’ve gotten the roots converted to fractional exponents there really isn’t too much to do other than to evaluate the integral.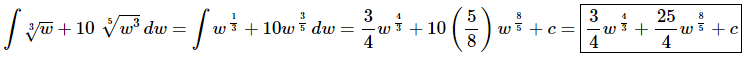
Don’t forget to add on the “+c” since we know that we are asking what function did we differentiate to get the integrand and the derivative of a constant is zero and so we do need to add that onto the answer.
Q.7. Evaluate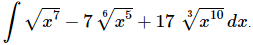
Ans. We first need to convert the roots to fractional exponents.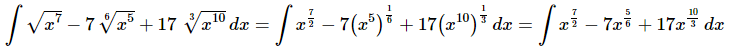
Once we’ve gotten the roots converted to fractional exponents there really isn’t too much to do other than to evaluate the integral.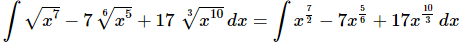
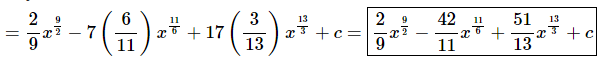
Don’t forget to add on the “+c” since we know that we are asking what function did we differentiate to get the integrand and the derivative of a constant is zero and so we do need to add that onto the answer.
Q.8. Evaluate 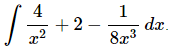
Ans. We first need to move the xx’s in the denominator to the numerator with negative exponents.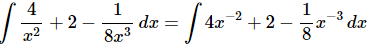
Remember that the “8” in the denominator of the third term stays in the denominator and does not move up with the x.
Once we’ve gotten the x’s out of the denominator there really isn’t too much to do other than to evaluate the integral.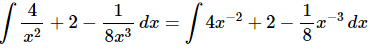
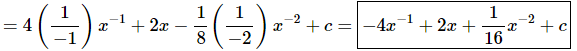
Don’t forget to add on the “+c” since we know that we are asking what function did we differentiate to get the integrand and the derivative of a constant is zero and so we do need to add that onto the answer.
Q.9. Evaluate 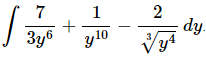
Ans. We first need to convert the root to a fractional exponent and move the y’s in the denominator to the numerator with negative exponents.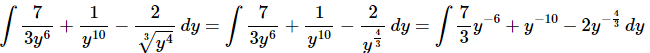
Remember that the “3” in the denominator of the first term stays in the denominator and does not move up with the y.
Once we’ve gotten the root converted to a fractional exponent and the yy’s out of the denominator there really isn’t too much to do other than to evaluate the integral.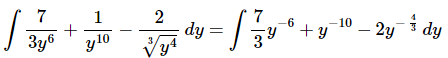
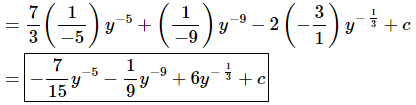
Don’t forget to add on the “+c” since we know that we are asking what function did we differentiate to get the integrand and the derivative of a constant is zero and so we do need to add that onto the answer.
Q.10. Evaluate 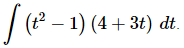
Ans. Since there is no “Product Rule” for integrals we’ll need to multiply the terms out prior to integration.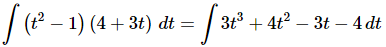
At this point there really isn’t too much to do other than to evaluate the integral.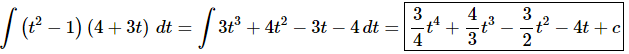
Don’t forget to add on the “+c” since we know that we are asking what function did we differentiate to get the integrand and the derivative of a constant is zero and so we do need to add that onto the answer.
Q.11. Evaluate 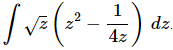
Ans. Since there is no “Product Rule” for integrals we’ll need to multiply the terms out prior to integration.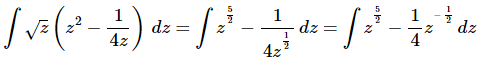
Don’t forget to convert the root to a fractional exponent and move the z’s out of the denominator.
At this point there really isn’t too much to do other than to evaluate the integral.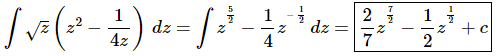
Don’t forget to add on the “+c” since we know that we are asking what function did we differentiate to get the integrand and the derivative of a constant is zero and so we do need to add that onto the answer.
Q.12. Evaluate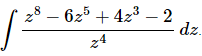
Ans. Since there is no “Quotient Rule” for integrals we’ll need to break up the integrand and simplify a little prior to integration.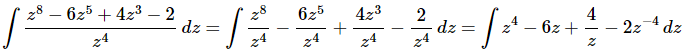
At this point there really isn’t too much to do other than to evaluate the integral.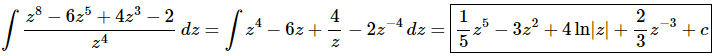
Don’t forget to add on the “+c” since we know that we are asking what function did we differentiate to get the integrand and the derivative of a constant is zero and so we do need to add that onto the answer.
Q.13. Evaluate 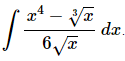
Ans. Since there is no “Quotient Rule” for integrals we’ll need to break up the integrand and simplify a little prior to integration.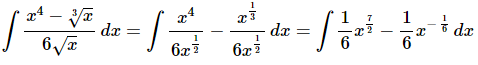
Don’t forget to convert the roots to fractional exponents!
At this point there really isn’t too much to do other than to evaluate the integral.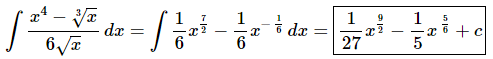
Don’t forget to add on the “+c” since we know that we are asking what function did we differentiate to get the integrand and the derivative of a constant is zero and so we do need to add that onto the answer.
Q.14. Evaluate 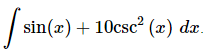
Ans. There really isn’t too much to do other than to evaluate the integral.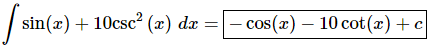
Don’t forget to add on the “+c” since we know that we are asking what function did we differentiate to get the integrand and the derivative of a constant is zero and so we do need to add that onto the answer.
Q.15. Evaluate
Ans. There really isn’t too much to do other than to evaluate the integral.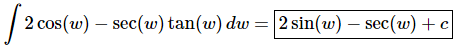
Don’t forget to add on the “+c” since we know that we are asking what function did we differentiate to get the integrand and the derivative of a constant is zero and so we do need to add that onto the answer.
Q.16. Evaluate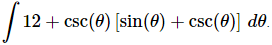
Ans. Before doing the integral we need to multiply out the product and don’t forget the definition of cosecant in terms of sine.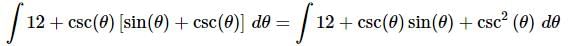
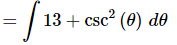
Recall that,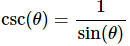
and so,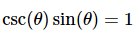
Doing this allows us to greatly simplify the integrand and, in fact, allows us to actually do the integral. Without this simplification we would not have been able to integrate the second term with the knowledge that we currently have.
At this point there really isn’t too much to do other than to evaluate the integral.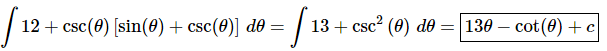
Don’t forget that with trig functions some terms can be greatly simplified just by recalling the definition of the trig functions and/or their relationship with the other trig functions.
Q.17. Evaluate 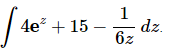
Ans. There really isn’t too much to do other than to evaluate the integral.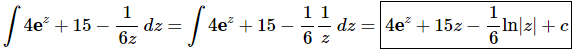
Be careful with the “6” in the denominator of the third term. The “best” way of dealing with it in this case is to split up the third term as we’ve done above and then integrate.
Note that the “best” way to do a problem is always relative for many Calculus problems. There are other ways of dealing with this term (later section material) and so what one person finds the best another may not. For us, this seems to be an easy way to deal with the 6 and not overly complicate the integration process.
Q.18. Evaluate 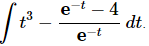
Ans. Before doing the integral we need to break up the quotient and do some simplification.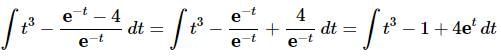
Make sure that you correctly distribute the minus sign when breaking up the second term and don’t forget to move the exponential in the denominator of the third term (after splitting up the integrand) to the numerator and changing the sign on the t to a “+” in the process.
At this point there really isn’t too much to do other than to evaluate the integral.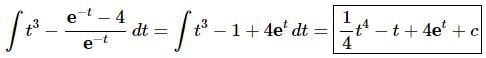
Q.19. Evaluate 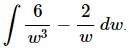
Ans. There really isn’t too much to do other than to evaluate the integral.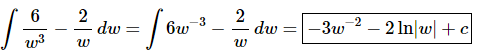
Q.20. Evaluate 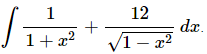
Ans. There really isn’t too much to do other than to evaluate the integral.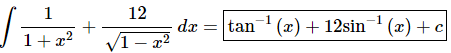
Note that because of the similarity of the derivative of inverse sine and inverse cosine an alternate answer is,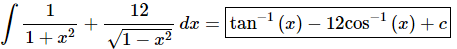
Q.21. Evaluate 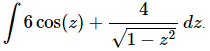
Ans. There really isn’t too much to do other than to evaluate the integral.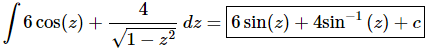
Note that because of the similarity of the derivative of inverse sine and inverse cosine an alternate answer is,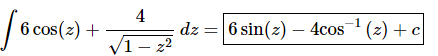
Q.22. Determine f(x) given that 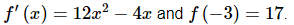
Ans. Recall from the notes in this section that we saw,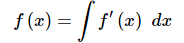
and so to arrive at a general formula for f(x) all we need to do is integrate the derivative that we’ve been given in the problem statement.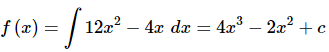
Don’t forget the “+c”!
Because we have the condition that f(−3)=17 we can just plug x=−3 into our answer from the previous step, set the result equal to 17 and solve the resulting equation for c.
Doing this gives,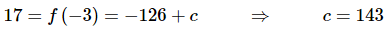
The function is then,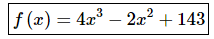
Q.23. Determine g(z)g(z) given that g 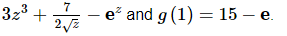
Ans. Recall from the notes in this section that we saw,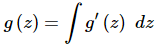
and so to arrive at a general formula for g(z) all we need to do is integrate the derivative that we’ve been given in the problem statement.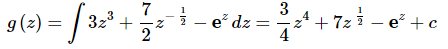
Don’t forget the “+c”!
Because we have the condition that g(1)=15−e we can just plug z=1 into our answer from the previous step, set the result equal to 15–e and solve the resulting equation for c.Doing this gives,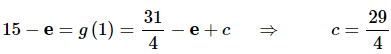
The function is then,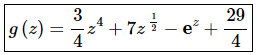
Q. 24. Determine h(t) given that 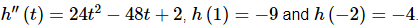
Ans. Because we know that the 2nd derivative is just the derivative of the 1st derivative we know that,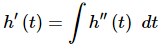
and so to arrive at a general formula for h′(t)h′(t) all we need to do is integrate the 2nd derivative that we’ve been given in the problem statement.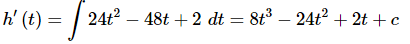
Don’t forget the “+c”!
Now, just as we did in the previous two problems, all that we need to do is integrate the 1st derivative (which we found in the first step) to determine a general formula for h(t)h(t).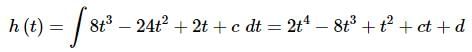
Don’t forget that cc is just a constant and so it will integrate just like we were integrating 2 or 4 or any other number. Also, the constant of integration from this step is liable to be different that the constant of integration from the first step and so we’ll need to make sure to call it something different, d in this case.
Now, we know the value of the function at two values of z. So let’s plug both of these into the general formula for h(t) that we found in the previous step to get,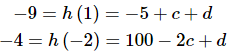
Solving this system of equations (you do remember your Algebra class right?) for c and d gives,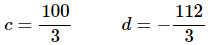
The function is then,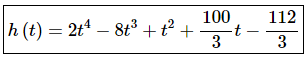
|
112 videos|65 docs|3 tests
|
FAQs on Computing Indefinite Integrals - Calculus - Mathematics
| 1. What is an indefinite integral? |  |
| 2. How do you compute an indefinite integral? |  |
| 3. What are the basic rules for computing indefinite integrals? |  |
| 4. Can you provide an example of computing an indefinite integral? |  |
| 5. Are there any special cases or exceptions in computing indefinite integrals? |  |
















