Introduction to Trigonometric Functions | Additional Topics for IIT JAM Mathematics PDF Download
Introducing Sine, Cosine and Tangent
There are three basic functions in trigonometry, each of which is one side of a right-angled triangle divided by another.
The three functions are:
| Name | Abbreviation | Relationship to sides of the triangle |
| Sine | Sin | Sin (θ) = Opposite/hypotenuse |
| Cosine | Cos | Cos (θ) = Adjacent/hypotenuse |
| Tangent | Tan | Tan (θ) = Opposite/adjacent |
Calculating Sine, Cosine and Tangent
Top Tip!
Because of the relationships between them, Tan θ can also be calculated as:
Sin θ/Cos θ.
This means that:
- Sin θ = Cos θ × Tan θ and
- Cos θ = Sin θ / Tan θ.
Trigonometry in a Circle
Consider a circle, divided into four quadrants.
Conventionally, the centre of the circle is considered as a Cartesian coordinate of (0,0). That is, the x value is 0 and the y value is 0.
Anything to the left of the centre has an x value of less than 0, or is negative, while anything to the right has a positive value.
Similarly anything below the centre point has a y value of less than 0, or is negative and any point in the top of the circle has a positive y value.
Now consider what happens if we draw a radius from the centre of the circle, due east if the circle were a compass. Marked 1 in the diagram.
If we then rotate the radius around the circle in an anticlockwise direction, it will create a series of triangles:

At point 2, a right-angled triangle can be seen. θ is around 60°.Sin θ is the opposite (the red line)/the hypotenuse (blue). Cos θ is the adjacent (the green line) over the hypotenuse (blue).
At point 3, θ is an obtuse angle, between 90° and 180°. Sin θ is the red line over the hypotenuse, and will therefore be positive. Cos θ, however, being the green line over the hypotenuse, will be negative since the green line is negative to the left of 0.
As you rotate the radius around the circle, the other two internal angles and the length of the other two sides all change and therefore affect the value of the sin and cos.
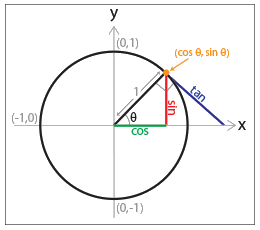
The Unit Circle
A 'Unit Circle' has a radius of 1.
When working with a unit circle we can measure cos, sin and tan directly:
Graphs of Sine, Cosine and Tangent
The relationship between the angle and the sin or cos can be drawn as a graph:
y = sin (x)
y = cos (x)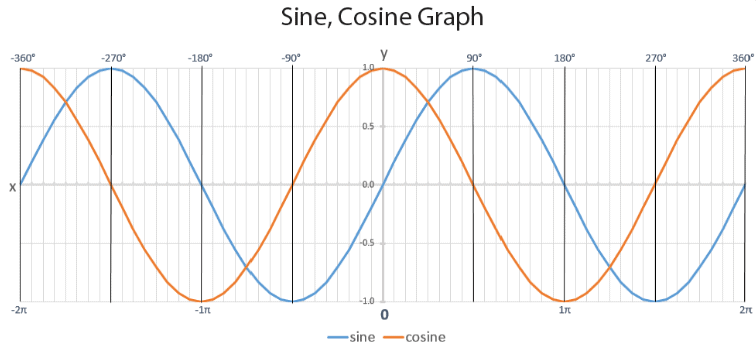
You can see that when x (i.e. the internal angle) is 0, then so is sin, which makes sense when you look at the circle above. This represents point (1), where there is basically no triangle.
Cosine is a simple shape to sine, but starts at 1 when x = 0, instead of 0.
Tangent is quite different. It moves from −∞ to +∞ crossing through 0 every 180°: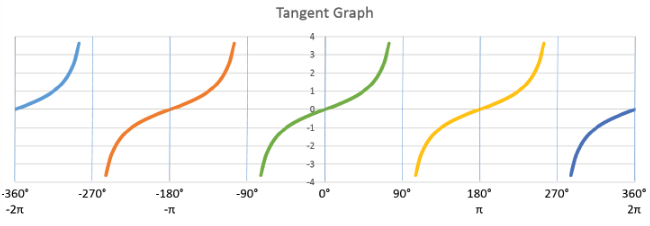
At infinity (positive or negative) it is said to be undefined.
You can also work out the inverse function to sin, cos and tan, which basically means 1 divided by that function. They are designated as sin/cos/tan -1. This enables you to work out the angle if you have the sin, cos or tan of it.
In other words:
Sin (90) = 1.
Sin−1 (1) = 90°
Trigonometry and Calculators
Scientific calculators have sin, cos, and tan functions, as well as inverse functions. It’s worth taking a few minutes to work out how your calculator operates, as this could save you hours of messing about when you need it.
Other Triangles and Trigonometry
Trigonometry also works for other triangles, just not in quite the same way. Instead there are two rules based on a triangle like this:

The Sine rule is:
a/sin A = b/sin B = c/sin C
The Cosine Rule is:
c2 = a2 + b2 – 2ab cos (C)
Why Do I Need Trigonometry?
This is a reasonable question, and the answer is at least partly because those who decide the mathematics curriculum in many countries think that you should know about it.
However, it does also have a few real-life functions, perhaps the most obvious of which is navigation, especially for boats.
Trigonometry and Navigation
When you are sailing or cruising at sea, where you end up is affected by:
- The direction in which you steer;
- The speed at which you travel in that direction (i.e. the motor or windspeed); and
- The direction and speed of the tide.
You can be motoring in one direction, but the tide could be coming from one side, and push you to the other. You will (ta-da!) need trigonometry to work out how far you will travel and in what precise direction.

You will, quite rightly, have worked out that it’s not quite as simple as all that, because the actual direction of travel depends on the tide speed and your speed, but you can probably see why trigonometry might be important!
Worked Example
You are out for a day’s sailing, and don’t really mind where you end up. You started out heading due east, and plan to sail for one hour at a cruising speed of 10 km/h. The tide is due north, and running at 5km/h. What direction will you end up travelling in?
1. First draw your triangle, and label the sides. You are heading due east, so let’s make that the bottom of the triangle, length 10km. The tide is going to push you north, so let’s make that the right hand side. And you want to know what direction you’ll end up going in, so that’s angle θ.
2. You have the opposite and the adjacent, which means that you need to use tan. Tan θ = Opposite/adjacent = 5/10 = 0.5.
3. Now is the time to use the inverse tan function. The inverse tan of 0.5 is 26.6°. In other words, tan 26.6 = 0.5.
4.Direction is measured from North, which is 0°. Your answer from (3), however, is measured from 90°, or East. You will therefore need to subtract your answer from 90°, to obtain the answer that you are travelling in a direction of 63.4°, which is between North East (45°) and East North East (67.5°).
FAQs on Introduction to Trigonometric Functions - Additional Topics for IIT JAM Mathematics
| 1. What are trigonometric functions? |  |
| 2. How are trigonometric functions used in mathematics? |  |
| 3. What is the unit circle and how is it related to trigonometric functions? |  |
| 4. How do trigonometric functions relate to right triangles? |  |
| 5. Can trigonometric functions be used to solve real-world problems? |  |

|
Explore Courses for Mathematics exam
|

|

















