Periodic Functions and Orthogonal Functions | Calculus - Mathematics PDF Download
This is going to be a short section. We just need to have a brief discussion about a couple of ideas that we’ll be dealing with on occasion as we move into the next topic of this chapter.
Periodic Function
The first topic we need to discuss is that of a periodic function. A function is said to be periodic with period T
if the following is true,
f(x+T)=f(x)for all x
The following is a nice little fact about periodic functions.
Fact 1
If f and g are both periodic functions with period T then so is f+g and fg.
This is easy enough to prove so let’s do that.
(f+g)(x+T)=f(x+T)+g(x+T)=f(x)+g(x)=(f+g)(x)
(fg)(x+T)=f(x+T)g(x+T)=f(x)g(x)=(fg)(x)
The two periodic functions that most of us are familiar are sine and cosine and in fact we’ll be using these two functions regularly in the remaining sections of this chapter. So, having said that let’s close off this discussion of periodic functions with the following fact,
Fact 2
sin(ωx) and cos(ωx) are periodic functions with period
Even and Odd Functions
The next quick idea that we need to discuss is that of even and odd functions.
Recall that a function is said to be even if,
f(−x)=f(x) and a function is said to be odd if,
f(−x)=−f(x)
The standard examples of even functions are f(x)=x2 and g(x)=cos(x) while the standard examples of odd functions are f(x)=x3 and g(x)=sin(x). The following fact about certain integrals of even/odd functions will be useful in some of our work.
Fact 3
1. If f(x) is an even function then,
2. If f(x) is an odd function then,
Note that this fact is only valid on a “symmetric” interval, i.e. an interval in the form [−L,L]. If we aren’t integrating on a “symmetric” interval then the fact may or may not be true.
Orthogonal Functions
The final topic that we need to discuss here is that of orthogonal functions. This idea will be integral to what we’ll be doing in the remainder of this chapter and in the next chapter as we discuss one of the basic solution methods for partial differential equations.
Let’s first get the definition of orthogonal functions out of the way.
Definition
1. Two non-zero functions, f(x) and g(x), are said to be orthogonal on a≤x≤b if,
2. A set of non-zero functions, {fi(x)}, is said to be mutually orthogonal on a≤x≤b (or just an orthogonal set if we’re being lazy) if fi(x) and fj(x) are orthogonal for every i≠j. In other words,
Note that in the case of i=j for the second definition we know that we’ll get a positive value from the integral because, 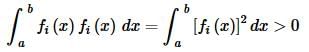
Recall that when we integrate a positive function we know the result will be positive as well.
Also note that the non-zero requirement is important because otherwise the integral would be trivially zero regardless of the other function we were using.
Before we work some examples there are a nice set of trig formulas that we’ll need to help us with some of the integrals.
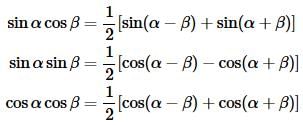
Now let’s work some examples that we’ll need over the course of the next couple of sections.
Example 1 Show that 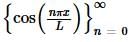 is mutually orthogonal on −L≤x≤L.
is mutually orthogonal on −L≤x≤L.
Solution:
This is not too difficult to do. All we really need to do is evaluate the following integral.
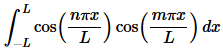
Before we start evaluating this integral let’s notice that the integrand is the product of two even functions and so must also be even. This means that we can use Fact 3 above to write the integral as,
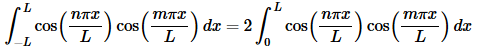
There are two reasons for doing this. First having a limit of zero will often make the evaluation step a little easier and that will be the case here. We’ll discuss the second reason after we’re done with the example.
Now, in order to do this integral we’ll actually need to consider three cases.
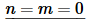
In this case the integral is very easy and is,
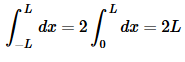
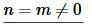
This integral is a little harder than the first case, but not by much (provided we recall a simple trig formula). The integral for this case is,
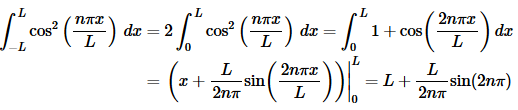
Now, at this point we need to recall that n is an integer and so sin(2nπ)=0 and our final value for the integral is,
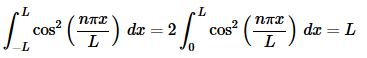
The first two cases are really just showing that if n=m the integral is not zero (as it shouldn’t be) and depending upon the value of n (and hence m) we get different values of the integral. Now we need to do the third case and this, in some ways, is the important case since we must get zero out of this integral in order to know that the set is an orthogonal set. So, let’s take care of the final case.
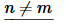
This integral is the “messiest” of the three that we’ve had to do here. Let’s just start off by writing the integral down.
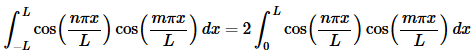
In this case we can’t combine/simplify as we did in the previous two cases. We can however, acknowledge that we’ve got a product of two cosines with different arguments and so we can use one of the trig formulas above to break up the product as follows,
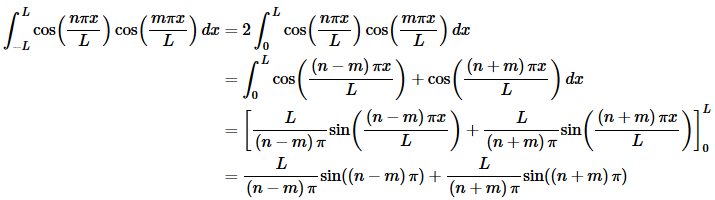
Now, we know that n and m are both integers and so n−m and n+m are also integers and so both of the sines above must be zero and all together we get,
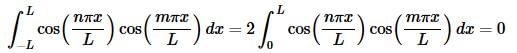
So, we’ve shown that if n≠m the integral is zero and if n=m the value of the integral is a positive constant and so the set is mutually orthogonal.
In all of the work above we kept both forms of the integral at every step. Let’s discuss why we did this a little bit. By keeping both forms of the integral around we were able to show that not only is 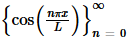 mutually orthogonal on −L≤x≤L but it is also mutually orthogonal on 0≤x≤L. The only difference is the value of the integral when n=m and we can get those values from the work above.
mutually orthogonal on −L≤x≤L but it is also mutually orthogonal on 0≤x≤L. The only difference is the value of the integral when n=m and we can get those values from the work above.
Let’s take a look at another example.
Example 2 Show that 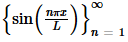 is mutually orthogonal on −L≤x≤L and on 0≤x≤L.
is mutually orthogonal on −L≤x≤L and on 0≤x≤L.
Solution:
First, we’ll acknowledge from the start this time that we’ll be showing orthogonality on both of the intervals. Second, we need to start this set at n=1 because if we used n=0 the first function would be zero and we don’t want the zero function to show up on our list.
As with the first example all we really need to do is evaluate the following integral.
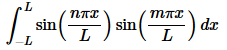
In this case integrand is the product of two odd functions and so must be even. This means that we can again use Fact 3 above to write the integral as,
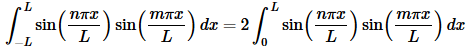
We only have two cases to do for the integral here.
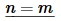
Not much to this integral. It’s pretty similar to the previous examples second case.
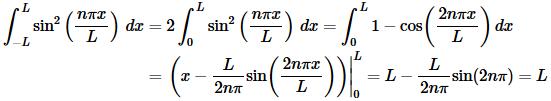
Summarizing up we get,
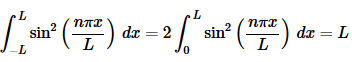
As with the previous example this can be a little messier but it is also nearly identical to the third case from the previous example so we’ll not show a lot of the work.
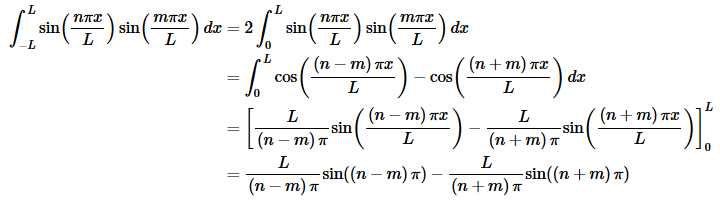
As with the previous example we know that n and m are both integers a and so both of the sines above must be zero and all together we get,
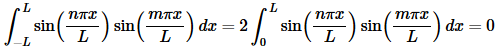
So, we’ve shown that if n≠m the integral is zero and if n=m the value of the integral is a positive constant and so the set is mutually orthogonal.
We’ve now shown that 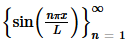 is mutually orthogonal on −L≤x≤L and on 0≤x≤L.
is mutually orthogonal on −L≤x≤L and on 0≤x≤L.
We need to work one more example in this section.
Example 3 Show that 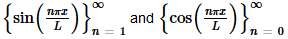 are mutually orthogonal on −L≤x≤L.
are mutually orthogonal on −L≤x≤L.
Solution:
We’ve now worked three examples here dealing with orthogonality and we should note that these were not just pulled out of the air as random examples to work. In the following sections (and following chapter) we’ll need the results from these examples. So, let’s summarize those results up here.
are mutually orthogonal on −L≤x≤L as individual sets and as a combined set.
is mutually orthogonal on 0≤x≤L.
is mutually orthogonal on 0≤x≤L.
We will also be needing the results of the integrals themselves, both on −L≤x≤L and on 0≤x≤L so let’s also summarize those up here as well so we can refer to them when we need to.
With this summary we’ll leave this section and move off into the second major topic of this chapter : Fourier Series.
|
112 videos|65 docs|3 tests
|
FAQs on Periodic Functions and Orthogonal Functions - Calculus - Mathematics
| 1. What is a periodic function? |  |
| 2. Can you provide an example of a periodic function? |  |
| 3. What are the key properties of periodic functions? |  |
| 4. What is the difference between a periodic function and an orthogonal function? |  |
| 5. How are periodic functions and orthogonal functions related in Fourier series? |  |





















