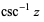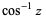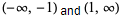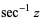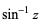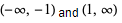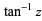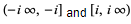Baics of Inverse Trigonometric Functions | Additional Topics for IIT JAM Mathematics PDF Download
The inverse trigonometric functions are the inverse functions of the trigonometric functions, written cos-1z, cot-1z, csc-1z, sec-1z, sin-1z, and tan-1z.
Alternate notations are sometimes used, as summarized in the following table.
f(z) | alternate notations |
cos-1 z | arccos z (Spanier and Oldham 1987, p. 333; Gradshteyn and Ryzhik 2000, p. 207) |
cot-1 z | arccot z (Spanier and Oldham 1987, p. 333), arcctg z (Spanier and Oldham 1987, p. 333; Gradshteyn and Ryzhik 2000, p. 208; Jeffrey 2000, p. 127) |
csc-1 z | arccsc z (Spanier and Oldham 1987, p. 333), arccosec z (Spanier and Oldham 1987, p. 333; Gradshteyn and Ryzhik 2000, p. 207) |
sec-1 z | arcsec z (Spanier and Oldham 1987, p. 333; Gradshteyn and Ryzhik 2000, p. 209) |
sin-1 z | arcsin z (Spanier and Oldham 1987, p. 333; Gradshteyn and Ryzhik 2000, p. 207) |
tan-1 z | arctan z (Spanier and Oldham 1987, p. 333), arctg z (Spanier and Oldham 1987, p. 333; Gradshteyn and Ryzhik 2000, p. 208; Jeffrey 2000, p. 127) |
The inverse trigonometric functions are multivalued. For example, there are multiple values of w such that z=sinw, so sin-1 z is not uniquely defined unless a principal value is defined. Such principal values are sometimes denoted with a capital letter so, for example, the principal value of the inverse sine sin-1 z may be variously denoted Sin-1 z or Arcsin z (Beyer 1987, p. 141). On the other hand, the notation sin-1 z (etc.) is also commonly used denote either the principal value or any quantity whose sine is z an (Zwillinger 1995, p. 466).
Worse still, the principal value and multiply valued notations are sometimes reversed, with for example arcsinz denoting the principal value and Arcsinz denoting the multivalued functions (Spanier and Oldham 1987, p. 333).
Since the inverse trigonometric functions are multivalued, they require branch cuts in the complex plane. Differing branch cut conventions are possible, but those adopted in this work follow those used by the Wolfram Language, summarized below.
function name | function | Wolfram Language | branch cut(s) |
inverse cosecant |
| ArcCsc[z] | (-1, 1) |
inverse cosine |
| ArcCos[z] |
|
inverse cotangent |
| ArcCot[z] | (-i, i) |
inverse secant |
| ArcSec[z] | (-1, 1) |
inverse sine |
| ArcSin[z] | |
inverse tangent |
| ArcTan[z] | |
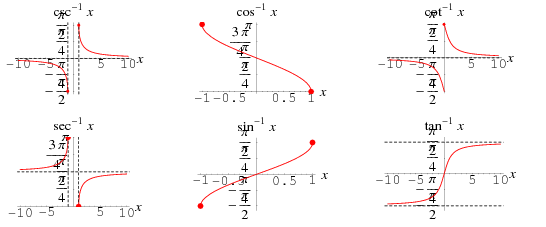
Different conventions are possible for the range of these functions for real arguments. Following the convention used by the Wolfram Language, the inverse trigonometric functions defined in this work have the following ranges for domains on the real line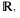 illustrated above.
illustrated above.
| function name | function | domain | range |
| inverse cosecant | 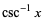 | (-∞, ∞) | 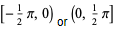 |
| inverse cosine | 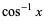 | [-1, 1] | 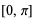 |
| inverse cotangent |  | (-∞, ∞) | 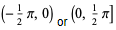 |
| inverse secant |  | (-∞, ∞) | 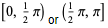 |
| inverse sine | 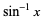 | [-1, 1] | 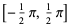 |
| inverse tangent | 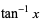 | (-∞, ∞) | 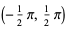 |
Inverse-forward identities are
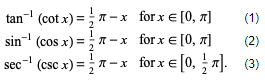
Forward-inverse identities are
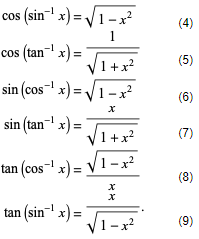
Inverse sum identities include
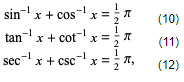
where equation (11) is valid only for x >0.
Complex inverse identities in terms of natural logarithms include
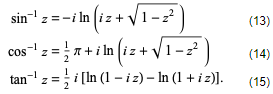
FAQs on Baics of Inverse Trigonometric Functions - Additional Topics for IIT JAM Mathematics
| 1. What are inverse trigonometric functions? |  |
| 2. How do inverse trigonometric functions work? |  |
| 3. What is the range of inverse trigonometric functions? |  |
| 4. How can inverse trigonometric functions be used in solving equations? |  |
| 5. Are there any important properties of inverse trigonometric functions? |  |

|
Explore Courses for Mathematics exam
|

|