Differentiation Formulas | Calculus - Mathematics PDF Download
In the first section of this chapter we saw the definition of the derivative and we computed a couple of derivatives using the definition. As we saw in those examples there was a fair amount of work involved in computing the limits and the functions that we worked with were not terribly complicated.
For more complex functions using the definition of the derivative would be an almost impossible task. Luckily for us we won’t have to use the definition terribly often. We will have to use it on occasion, however we have a large collection of formulas and properties that we can use to simplify our life considerably and will allow us to avoid using the definition whenever possible.
We will introduce most of these formulas over the course of the next several sections. We will start in this section with some of the basic properties and formulas. We will give the properties and formulas in this section in both “prime” notation and “fraction” notation.
Properties
In other words, to differentiate a sum or difference all we need to do is differentiate the individual terms and then put them back together with the appropriate signs. Note as well that this property is not limited to two functions.
See the Proof of Various Derivative Formulas section of the Extras chapter to see the proof of this property. It’s a very simple proof using the definition of the derivative.
is any number
In other words, we can “factor” a multiplicative constant out of a derivative if we need to. See the Proof of Various Derivative Formulas section of the Extras chapter to see the proof of this property.
Note that we have not included formulas for the derivative of products or quotients of two functions here. The derivative of a product or quotient of two functions is not the product or quotient of the derivatives of the individual pieces. We will take a look at these in the next section.
Next, let’s take a quick look at a couple of basic “computation” formulas that will allow us to actually compute some derivatives.
Formulas
The derivative of a constant is zero. See the Proof of Various Derivative Formulas section of the Extras chapter to see the proof of this formula.
This formula is sometimes called the power rule. All we are doing here is bringing the original exponent down in front and multiplying and then subtracting one from the original exponent.
Note as well that in order to use this formula n must be a number, it can’t be a variable. Also note that the base, the x, must be a variable, it can’t be a number. It will be tempting in some later sections to misuse the Power Rule when we run in some functions where the exponent isn’t a number and/or the base isn’t a variable.
See the Proof of Various Derivative Formulas section of the Extras chapter to see the proof of this formula. There are actually three different proofs in this section. The first two restrict the formula to n being an integer because at this point that is all that we can do at this point. The third proof is for the general rule but does suppose that you’ve read most of this chapter.
These are the only properties and formulas that we’ll give in this section. Let’s compute some derivatives using these properties.
Example 1 Differentiate each of the following functions.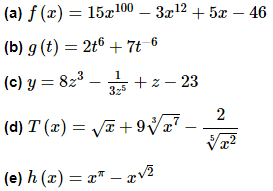
Solution:
(a) f(x) = 15x100 − 3x12 + 5x − 46
In this case we have the sum and difference of four terms and so we will differentiate each of the terms using the first property from above and then put them back together with the proper sign. Also, for each term with a multiplicative constant remember that all we need to do is “factor” the constant out (using the second property) and then do the derivative.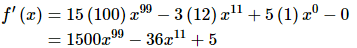
Notice that in the third term the exponent was a one and so upon subtracting 1 from the original exponent we get a new exponent of zero. Now recall that x0 = 1. Don’t forget to do any basic arithmetic that needs to be done such as any multiplication and/or division in the coefficients.
(b) g(t) = 2t6 + 7t−6
The point of this problem is to make sure that you deal with negative exponents correctly. Here is the derivative.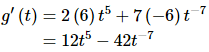
Make sure that you correctly deal with the exponents in these cases, especially the negative exponents. It is an easy mistake to “go the other way” when subtracting one off from a negative exponent and get −6t−5 instead of the correct −6t−7.
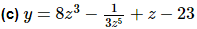
Now in this function the second term is not correctly set up for us to use the power rule. The power rule requires that the term be a variable to a power only and the term must be in the numerator. So, prior to differentiating we first need to rewrite the second term into a form that we can deal with.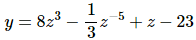
Note that we left the 3 in the denominator and only moved the variable up to the numerator. Remember that the only thing that gets an exponent is the term that is immediately to the left of the exponent. If we’d wanted the three to come up as well we’d have written,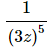
so be careful with this! It’s a very common mistake to bring the 3 up into the numerator as well at this stage.
Now that we’ve gotten the function rewritten into a proper form that allows us to use the Power Rule we can differentiate the function. Here is the derivative for this part.
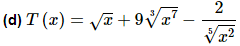
All of the terms in this function have roots in them. In order to use the power rule we need to first convert all the roots to fractional exponents. Again, remember that the Power Rule requires us to have a variable to a number and that it must be in the numerator of the term. Here is the function written in “proper” form.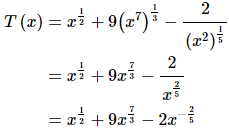
In the last two terms we combined the exponents. You should always do this with this kind of term. In a later section we will learn of a technique that would allow us to differentiate this term without combining exponents, however it will take significantly more work to do. Also, don’t forget to move the term in the denominator of the third term up to the numerator. We can now differentiate the function.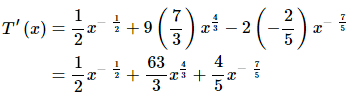
Make sure that you can deal with fractional exponents. You will see a lot of them in this class.
(e) h(x) = xπ − x√2
In all of the previous examples the exponents have been nice integers or fractions. That is usually what we’ll see in this class. However, the exponent only needs to be a number so don’t get excited about problems like this one. They work exactly the same.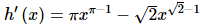
The answer is a little messy and we won’t reduce the exponents down to decimals. However, this problem is not terribly difficult it just looks that way initially.
There is a general rule about derivatives in this class that you will need to get into the habit of using. When you see radicals you should always first convert the radical to a fractional exponent and then simplify exponents as much as possible. Following this rule will save you a lot of grief in the future.
Back when we first put down the properties we noted that we hadn’t included a property for products and quotients. That doesn’t mean that we can’t differentiate any product or quotient at this point. There are some that we can do.
Example 2 Differentiate each of the following functions.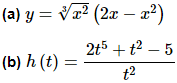
Solution: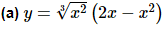
In this function we can’t just differentiate the first term, differentiate the second term and then multiply the two back together. That just won’t work. We will discuss this in detail in the next section so if you’re not sure you believe that hold on for a bit and we’ll be looking at that soon as well as showing you an example of why it won’t work.
It is still possible to do this derivative however. All that we need to do is convert the radical to fractional exponents (as we should anyway) and then multiply this through the parenthesis.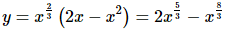
Now we can differentiate the function.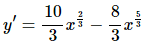

As with the first part we can’t just differentiate the numerator and the denominator and the put it back together as a fraction. Again, if you’re not sure you believe this hold on until the next section and we’ll take a more detailed look at this.
We can simplify this rational expression however as follows.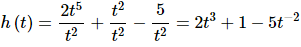
This is a function that we can differentiate.
h′(t) = 6t2+10t−3
So, as we saw in this example there are a few products and quotients that we can differentiate. If we can first do some simplification the functions will sometimes simplify into a form that can be differentiated using the properties and formulas in this section.
Before moving on to the next section let’s work a couple of examples to remind us once again of some of the interpretations of the derivative.
Example 3 Is 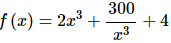 increasing, decreasing or not changing at x = −2?
increasing, decreasing or not changing at x = −2?
Solution:
We know that the rate of change of a function is given by the functions derivative so all we need to do is it rewrite the function (to deal with the second term) and then take the derivative.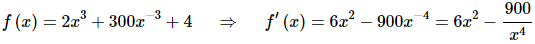
Note that we rewrote the last term in the derivative back as a fraction. This is not something we’ve done to this point and is only being done here to help with the evaluation in the next step. It’s often easier to do the evaluation with positive exponents.
So, upon evaluating the derivative we get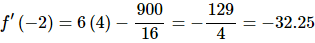
So, at x = −2 the derivative is negative and so the function is decreasing at x = −2.
Example 4 Find the equation of the tangent line to f(x) = 4x − 8√x at x = 16.
Solution:
We know that the equation of a tangent line is given by,
y = f(a) + f′(a)(x − a)
So, we will need the derivative of the function (don’t forget to get rid of the radical).
Again, notice that we eliminated the negative exponent in the derivative solely for the sake of the evaluation. All we need to do then is evaluate the function and the derivative at the point in question, x = 16.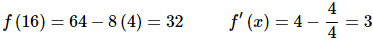
The tangent line is then,
y=32+3(x−16)=3x−16
Example 5 The position of an object at any time t (in hours) is given by,
s(t) = 2t3 − 21t2 + 60t − 10
Determine when the object is moving to the right and when the object is moving to the left.
Solution:
The only way that we’ll know for sure which direction the object is moving is to have the velocity in hand. Recall that if the velocity is positive the object is moving off to the right and if the velocity is negative then the object is moving to the left.
We need the derivative in order to get the velocity of the object. The derivative, and hence the velocity, is,
s′(t) = 6t2 − 42t + 60 = 6(t2 − 7t + 10) = 6(t − 2)(t − 5)
The reason for factoring the derivative will be apparent shortly.
Now, we need to determine where the derivative is positive and where the derivative is negative. There are several ways to do this. The method that we tend to prefer is the following.
Since polynomials are continuous we know from the Intermediate Value Theorem that if the polynomial ever changes sign then it must have first gone through zero. So, if we knew where the derivative was zero we would know the only points where the derivative might change sign.
We can see from the factored form of the derivative that the derivative will be zero at t=2 and t=5. Let’s graph these points on a number line.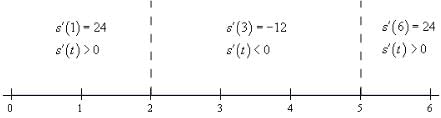
Now, we can see that these two points divide the number line into three distinct regions. In each of these regions we know that the derivative will be the same sign. Recall the derivative can only change sign at the two points that are used to divide the number line up into the regions.
Therefore, all that we need to do is to check the derivative at a test point in each region and the derivative in that region will have the same sign as the test point. Here is the number line with the test points and results shown.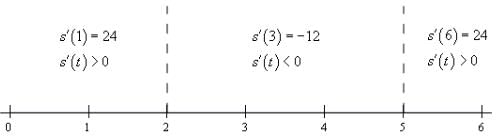
Here are the intervals in which the derivative is positive and negative.
positive: − ∞ < t < 2 & 5 < t < ∞
negative: 2 < t < 5
We included negative t’s here because we could even though they may not make much sense for this problem. Once we know this we also can answer the question. The object is moving to the right and left in the following intervals.
moving to the right: − ∞ < t < 2 & 5 < t < ∞
moving to the left: 2 < t < 5
Make sure that you can do the kind of work that we just did in this example. You will be asked numerous times over the course of the next two chapters to determine where functions are positive and/or negative. If you need some review or want to practice these kinds of problems you should check out the Solving Inequalities section of the Algebra/Trig Review.
Practice Problems: Differentiation Formulas
For problems 1 – 12 find the derivative of the given function.
1. Find the derivative of f(x) = 6x3 − 9x + 4.
Solution:
There isn’t much to do here other than take the derivative using the rules we discussed in this section.
f′(x) = 18x2 − 9
2. Find the derivative of y = 2t4 − 10t2 + 13t.
Solution:
There isn’t much to do here other than take the derivative using the rules we discussed in this section.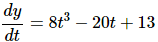
3. Find the derivative of g(z) = 4z7 − 3z−7 + 9z.
Solution:
There isn’t much to do here other than take the derivative using the rules we discussed in this section.
g′(z) = 28z6 + 21z−8 + 9
4. Find the derivative of h(y) = y−4 − 9y−3 + 8y−2 + 12.
Solution:
There isn’t much to do here other than take the derivative using the rules we discussed in this section.
h′(y) = −4y−5 + 27y−4 − 16y−3
5. Find the derivative of y = √x + 8 ∛x − 2 ∜x.
There isn’t much to do here other than take the derivative using the rules we discussed in this section.
Remember that you’ll need to convert the roots to fractional exponents before you start taking the derivative. Here is the rewritten function.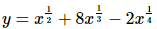
The derivative is,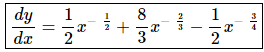
6. Find the derivative of 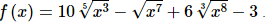
Solution:
There isn’t much to do here other than take the derivative using the rules we discussed in this section.
Remember that you’ll need to convert the roots to fractional exponents before you start taking the derivative. Here is the rewritten function.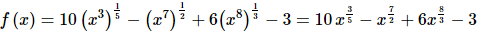
The derivative is,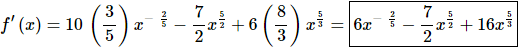
7. Find the derivative of 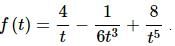
Solution:
There isn’t much to do here other than take the derivative using the rules we discussed in this section.
Remember that you’ll need to rewrite the terms so that each of the t’s are in the numerator with negative exponents before taking the derivative. Here is the rewritten function.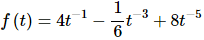
The derivative is,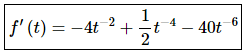
8. Find the derivative of 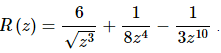
Solution:
There isn’t much to do here other than take the derivative using the rules we discussed in this section.
Remember that you’ll need to rewrite the terms so that each of the z’s are in the numerator with negative exponents and rewrite the root as a fractional exponent before taking the derivative. Here is the rewritten function.
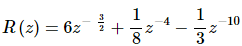
The derivative is,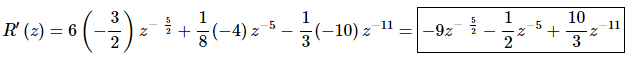
9. Find the derivative of z = x(3x2 − 9).
Solution:
There isn’t much to do here other than take the derivative using the rules we discussed in this section.
Remember that in order to do this derivative we’ll first need to multiply the function out before we take the derivative. Here is the rewritten function.
z = 3x3 − 9x
The derivative is,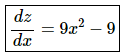
10. Find the derivative of g(y) = (y − 4) (2y + y2).
Solution:
There isn’t much to do here other than take the derivative using the rules we discussed in this section.
Remember that in order to do this derivative we’ll first need to multiply the function out before we take the derivative. Here is the rewritten function.
g(y) = y3 − 2y2 − 8y
The derivative is,
g′(y) = 3y2 − 4y − 8
11. Find the derivative of 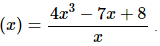
Solution:
There isn’t much to do here other than take the derivative using the rules we discussed in this section.
Remember that in order to do this derivative we’ll first need to divide the function out and simplify before we take the derivative. Here is the rewritten function.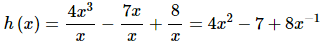
The derivative is,
h′(x) = 8x − 8x−2
12. Find the derivative of 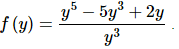
Solution:
There isn’t much to do here other than take the derivative using the rules we discussed in this section.
Remember that in order to do this derivative we’ll first need to divide the function out and simplify before we take the derivative. Here is the rewritten function.
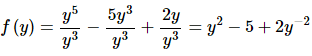
The derivative is, 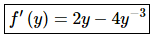
13. Determine where, if anywhere, the function f(x) = x3 + 9x2 − 48x + 2 is not changing.
Solution:
Step 1
Recall that one of the interpretations of the derivative is that it gives the rate of change of the function. So, the function won’t be changing if its rate of change is zero and so all we need to do is find the derivative and set it equal to zero to determine where the rate of change is zero and hence the function will not be changing.
First the derivative, and we’ll do a little factoring while we are at it.
f′(x) = 3x2 + 18x − 48 = 3(x2 + 6x − 16) = 3(x+8)(x−2)
Step 2
Now all that we need to do is set this equation to zero and solve.
We can easily see from this that the derivative will be zero at x=−8 and x=2. The function therefore not be changing at,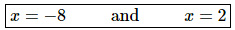
14. Determine where, if anywhere, the function y = 2z4 − z3 − 3z2 is not changing.
Solution:
Step 1
Recall that one of the interpretations of the derivative is that it gives the rate of change of the function. So, the function won’t be changing if its rate of change is zero and so all we need to do is find the derivative and set it equal to zero to determine where the rate of change is zero and hence the function will not be changing.
First the derivative, and we’ll do a little factoring while we are at it.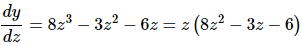
Step 2
Now all that we need to do is set this equation to zero and solve.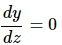

We can easily see from this that the derivative will be zero at z=0, however, because the quadratic doesn’t factor we’ll need to use the quadratic formula to determine where, if anywhere, that will be zero.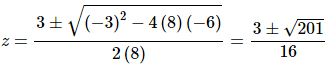

15. Find the tangent line to 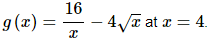
Solution:
Step 1
Recall that one of the interpretations of the derivative is that it gives slope of the tangent line to the graph of the function.
So, we’ll need the derivative of the function. However before doing that we’ll need to do a little rewrite. Here is that work as well as the derivative.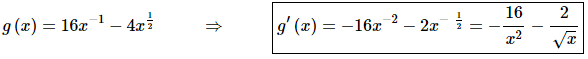
Note that we rewrote the derivative back into rational expressions with roots to help with the evaluation.
Step 2
Next we need to evaluate the function and derivative at x=4.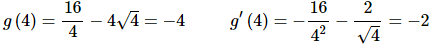
Step 3
Now all that we need to do is write down the equation of the tangent line.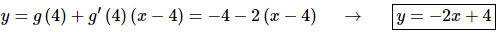
16. Find the tangent line to f(x) = 7x4 + 8x−6 + 2 x at x = −1.
Solution:
step 1
Recall that one of the interpretations of the derivative is that it gives slope of the tangent line to the graph of the function.
So, we’ll need the derivative of the function.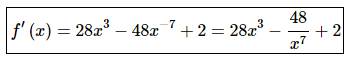
Note that we rewrote the derivative back into rational expressions help a little with the evaluation.
Step 2
Next we need to evaluate the function and derivative at x = −1.
Step 3
Now all that we need to do is write down the equation of the tangent line.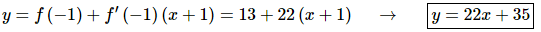
17. The position of an object at any time t is given by s(t) = 3t4 − 40t3 + 126t2 − 9.
(a) Determine the velocity of the object at any time t.
(b) Does the object ever stop changing?
(c) When is the object moving to the right and when is the object moving to the left?
Solution:
(a) Determine the velocity of the object at any time t.
Recall that one of the interpretations of the derivative is that it gives the velocity of an object if we know the position function of the object.
We’ve been given the position function of the object and so all we need to do is find its derivative and we’ll have the velocity of the object at any time t.
The velocity of the object is then,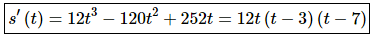
Note that the derivative was factored for later parts and doesn’t really need to be done in general.
(b) Does the object ever stop changing?
The object will not be moving if the velocity is ever zero and so all we need to do is set the derivative equal to zero and solve.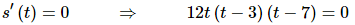
From this it is pretty easy to see that the derivative will be zero, and hence the object will not be moving, at,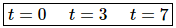
(c) When is the object moving to the right and when is the object moving to the left?
To answer this part all we need to know is where the derivative is positive (and hence the object is moving to the right) or negative (and hence the object is moving to the left). Because the derivative is continuous we know that the only place it can change sign is where the derivative is zero. So, as we did in this section a quick number line will give us the sign of the derivative for the various intervals.
Here is the number line for this problem.
From this we get the following right/left movement information.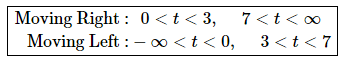
Note that depending upon your interpretation of t as time you may or may not have included the interval − ∞ < t < 0 in the “Moving Left” portion.
18. Determine where the function h(z) = 6 + 40z3 − 5z4 − 4z5 is increasing and decreasing.
Solution:
Step 1
Recall that one of the interpretations of the derivative is that it gives the rate of change of the function. Since we are talking about where the function is increasing and decreasing we are clearly talking about the rate of change of the function.
So, we’ll need the derivative.
Step 2
Next, we need to know where the function is not changing and so all we need to do is set the derivative equal to zero and solve.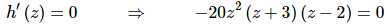
From this it is pretty easy to see that the derivative will be zero, and hence the function will not be moving, at,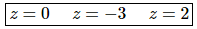
Step 3
To get the answer to this problem all we need to know is where the derivative is positive (and hence the function is increasing) or negative (and hence the function is decreasing). Because the derivative is continuous we know that the only place it can change sign is where the derivative is zero. So, as we did in this section a quick number line will give us the sign of the derivative for the various intervals.
Here is the number line for this problem.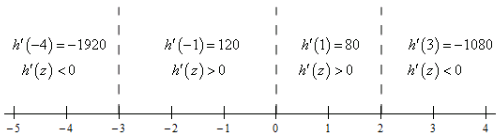
From this we get the following increasing/decreasing information.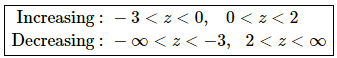
19. Determine where the function R(x) = (x + 1) (x − 2)2 is increasing and decreasing.
Solution:
Step 1
Recall that one of the interpretations of the derivative is that it gives the rate of change of the function. Since we are talking about where the function is increasing and decreasing we are clearly talking about the rate of change of the function.
So, we’ll need the derivative. First however we’ll need to multiply out the function so we can actually take the derivative. Here is the rewritten function and the derivative.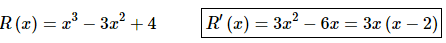
Note that the derivative was factored for later steps and doesn’t really need to be done in general.
Step 2
Next, we need to know where the function is not changing and so all we need to do is set the derivative equal to zero and solve.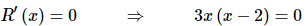
From this it is pretty easy to see that the derivative will be zero, and hence the function will not be moving, at,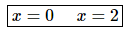
Step 3
To get the answer to this problem all we need to know is where the derivative is positive (and hence the function is increasing) or negative (and hence the function is decreasing). Because the derivative is continuous we know that the only place it can change sign is where the derivative is zero. So, as we did in this section a quick number line will give us the sign of the derivative for the various intervals.
Here is the number line for this problem.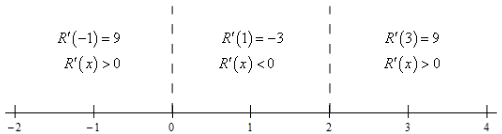
From this we get the following increasing/decreasing information.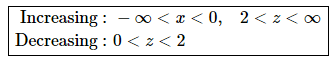
20. Determine where, if anywhere, the tangent line to f(x) = x3 − 5x2 + x is parallel to the line y = 4x + 23.
Solution:
Step 1
The first thing that we’ll need of course is the slope of the tangent line. So, all we need to do is take the derivative of the function.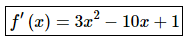
Step 2
Two lines that are parallel will have the same slope and so all we need to do is determine where the slope of the tangent line will be 4, the slope of the given line. In other words, we’ll need to solve,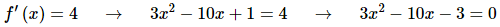
This quadratic doesn’t factor and so a quick use of the quadratic formula will solve this for us.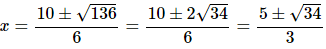
So, the tangent line will be parallel to y = 4x + 23 at,
|
112 videos|65 docs|3 tests
|
FAQs on Differentiation Formulas - Calculus - Mathematics
| 1. What are the basic rules of differentiation in mathematics? |  |
| 2. How does the power rule work in differentiation? |  |
| 3. What is the product rule in differentiation and how is it applied? |  |
| 4. How does the quotient rule work in differentiation? |  |
| 5. What is the chain rule in differentiation and when is it used? |  |





















