Product and Quotient Rule | Calculus - Mathematics PDF Download
In the previous section we noted that we had to be careful when differentiating products or quotients. It’s now time to look at products and quotients and see why.
First let’s take a look at why we have to be careful with products and quotients. Suppose that we have the two functions f(x) = x3 and g(x) = x6 . Let’s start by computing the derivative of the product of these two functions. This is easy enough to do directly.
(fg)′= (x3x6)′ = (x9)′=9x8
Remember that on occasion we will drop the (x) part on the functions to simplify notation somewhat. We’ve done that in the work above.
Now, let’s try the following.
f′(x)g′(x) = (3x2)(6x5) = 18x7
So, we can very quickly see that.
(fg)′ ≠ f′g′
In other words, the derivative of a product is not the product of the derivatives.
Using the same functions we can do the same thing for quotients.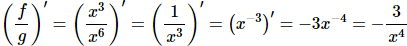

So, again we can see that,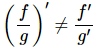
To differentiate products and quotients we have the Product Rule and the Quotient Rule.
Product Rule
If the two functions f(x) and g(x) are differentiable (i.e. the derivative exist) then the product is differentiable and,
(fg)′ = f′g + fg′
The proof of the Product Rule is shown in the Proof of Various Derivative Formulas section of the Extras chapter.
Quotient Rule
If the two functions f(x) and g(x) are differentiable (i.e. the derivative exist) then the quotient is differentiable and,
Note that the numerator of the quotient rule is very similar to the product rule so be careful to not mix the two up!
The proof of the Quotient Rule is shown in the Proof of Various Derivative Formulas section of the Extras chapter.
Let’s do a couple of examples of the product rule.
Example 1 Differentiate each of the following functions.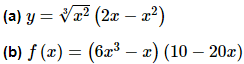
Solution:
At this point there really aren’t a lot of reasons to use the product rule. As we noted in the previous section all we would need to do for either of these is to just multiply out the product and then differentiate.
With that said we will use the product rule on these so we can see an example or two. As we add more functions to our repertoire and as the functions become more complicated the product rule will become more useful and in many cases required.
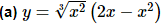
Note that we took the derivative of this function in the previous section and didn’t use the product rule at that point. We should however get the same result here as we did then.
Now let’s do the problem here. There’s not really a lot to do here other than use the product rule. However, before doing that we should convert the radical to a fractional exponent as always.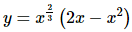
Now let’s take the derivative. So, we take the derivative of the first function times the second then add on to that the first function times the derivative of the second function.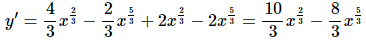
This is what we got for an answer in the previous section so that is a good check of the product rule.
(b) f (x) = (6x3 − x) (10 − 20x)
This one is actually easier than the previous one. Let’s just run it through the product rule.
f′(x) = (18x2−1)(10−20x) + (6x3−x)(−20) = −480x3 + 180x2 + 40x − 10
Since it was easy to do we went ahead and simplified the results a little.
Let’s now work an example or two with the quotient rule. In this case, unlike the product rule examples, a couple of these functions will require the quotient rule in order to get the derivative. The last two however, we can avoid the quotient rule if we’d like to as we’ll see.
Example 2 Differentiate each of the following functions.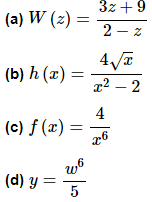
Solution:
There isn’t a lot to do here other than to use the quotient rule. Here is the work for this function.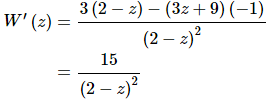
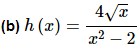
Again, not much to do here other than use the quotient rule. Don’t forget to convert the square root into a fractional exponent.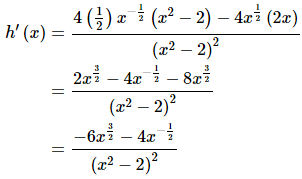
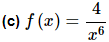
It seems strange to have this one here rather than being the first part of this example given that it definitely appears to be easier than any of the previous two. In fact, it is easier. There is a point to doing it here rather than first. In this case there are two ways to do compute this derivative. There is an easy way and a hard way and in this case the hard way is the quotient rule. That’s the point of this example.
Let’s do the quotient rule and see what we get.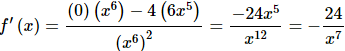
Now, that was the “hard” way. So, what was so hard about it? Well actually it wasn’t that hard, there is just an easier way to do it that’s all. However, having said that, a common mistake here is to do the derivative of the numerator (a constant) incorrectly. For some reason many people will give the derivative of the numerator in these kinds of problems as a 1 instead of 0! Also, there is some simplification that needs to be done in these kinds of problems if you do the quotient rule.
The easy way is to do what we did in the previous section.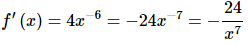
Either way will work, but I’d rather take the easier route if I had the choice.
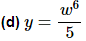
This problem also seems a little out of place. However, it is here again to make a point. Do not confuse this with a quotient rule problem. While you can do the quotient rule on this function there is no reason to use the quotient rule on this. Simply rewrite the function as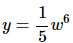
and differentiate as always.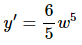
Finally, let’s not forget about our applications of derivatives.
Example 3 >Suppose that the amount of air in a balloon at any time t is given by
Determine if the balloon is being filled with air or being drained of air at t = 8.
Solution:
If the balloon is being filled with air then the volume is increasing and if it’s being drained of air then the volume will be decreasing. In other words, we need to get the derivative so that we can determine the rate of change of the volume at t=8.
This will require the quotient rule.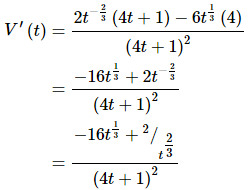
Note that we simplified the numerator more than usual here. This was only done to make the derivative easier to evaluate.
The rate of change of the volume at t=8 is then,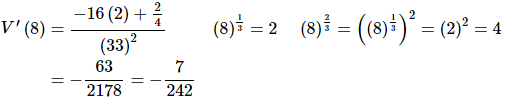
So, the rate of change of the volume at t=8 is negative and so the volume must be decreasing. Therefore, air is being drained out of the balloon at t=8.
As a final topic let’s note that the product rule can be extended to more than two functions, for instance.
(fgh)′=f′gh+fg′h+fgh′
(fghw)′=f′ghw+fg′hw+fgh′w+fghw′
Deriving these products of more than two functions is actually pretty simple. For example, let’s take a look at the three function product rule.
First, we don’t think of it as a product of three functions but instead of the product rule of the two functions fg and h which we can then use the two function product rule on. Doing this gives,
(fgh)′=([fg]h)′=[fg]′h+[fg]h′
Note that we put brackets on the fg part to make it clear we are thinking of that term as a single function. Now all we need to do is use the two function product rule on the [fg]′ term and then do a little simplification.
(fgh)′=[f′g+fg′]h+[fg]h′=f′gh+fg′h+fgh′
Any product rule with more functions can be derived in a similar fashion.
With this section and the previous section we are now able to differentiate powers of x as well as sums, differences, products and quotients of these kinds of functions. However, there are many more functions out there in the world that are not in this form. The next few sections give many of these functions as well as give their derivatives.
Practice Problems: Product And Quotient Rule
For problems 1 – 6 use the Product Rule or the Quotient Rule to find the derivative of the given function.
1. Use the Product Rule to find the derivative of f(t) = (4t2 − t) (t3 − 8t2 + 12).
Solution:
There isn’t much to do here other than take the derivative using the product rule.
f′(t) = (8t−1)(t3−8t2+12) + (4t2−t (3t2−16t) = 20t4 − 132t3 + 24t2 + 96t − 12
Note that we multiplied everything out to get a “simpler” answer.
2. Use the Product Rule to find the derivative of 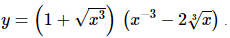
Solution:
There isn’t much to do here other than take the derivative using the product rule. We’ll also need to convert the roots to fractional exponents.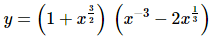
The derivative is then,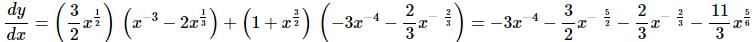
Note that we multiplied everything out to get a “simpler” answer.
3. Use the Product Rule to find the derivative of h(z) = (1 + 2z + 3z2) (5z + 8z2 − z3).
Solution:
There isn’t much to do here other than take the derivative using the product rule.
h′(z)=(2+6z)(5z+8z2−z3)+(1+2z+3z2)(5+16z−3z2)=5+36z+90z2+88z3−15z4
Note that we multiplied everything out to get a “simpler” answer.
4. Use the Quotient Rule to find the derivative of 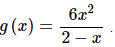
Solution:
There isn’t much to do here other than take the derivative using the quotient rule.
5. Use the Quotient Rule to find the derivative of 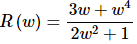
Solution:
There isn’t much to do here other than take the derivative using the quotient rule.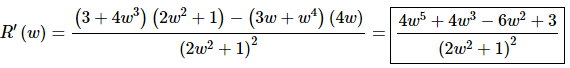
6. Use the Quotient Rule to find the derivative of 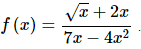
Solution:
There isn’t much to do here other than take the derivative using the quotient rule.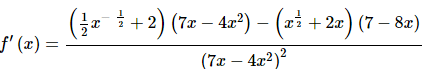
7. If f(2) = −8, f′(2) = 3, g(2) = 17 and g′(2) = −4 determine the value of (fg)′(2).
Solution:
We know that the product rule is,
(fg)′(x)=f′(x)g(x)+f(x)g′(x)
Now, we want to know the value of this at x=2 and so all we need to do is plug this into the derivative. Doing this gives,
(fg)′(2)=f′(2)g(2)+f(2)g′(2)
Now, we were given values for all these quantities and so all we need to do is plug these into our “formula” above.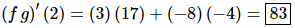
8. If f(x) = x3g(x), g(−7) = 2, g′(−7) = −9 determine the value of f′(−7).
Solution:
Even though we don’t know what g(x) is we do have a product of two functions here and so we can use the product rule to determine the derivative of f(x).
f′(x)=3x2g(x)+x3g′(x)
Now all we need to do is plug x = −7 into this and use the given information to determine the value of f′(−7).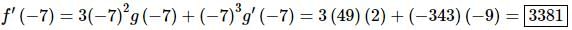
9. Find the equation of the tangent line to f(x) = (1 + 12√x)(4 − x2) at x = 9.
Solution:
Step 1
We know that the derivative of the function will give us the slope of the tangent line so we’ll need the derivative of the function. We’ll use the product rule to get the derivative.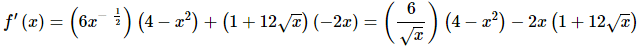
Step 2
Note that we didn’t bother to “simplify” the derivative (other than converting the fractional exponent back to a root) because all we really need this for is a quick evaluation.
Speaking of which here are the evaluations that we’ll need for this problem.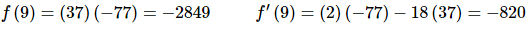
Step 3
Now all that we need to do is write down the equation of the tangent line.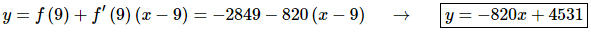
10. Determine where 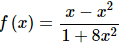 is increasing and decreasing.
is increasing and decreasing.
Solution:
Step 1
We’ll first need the derivative, which will require the quotient rule, because we know that the derivative will give us the rate of change of the function. Here is the derivative.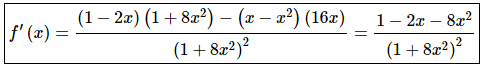
Step 2
Next, we need to know where the function is not changing and so all we need to do is set the derivative equal to zero and solve. In this case it is clear that the denominator will never be zero for any real number and so the derivative will only be zero where the numerator is zero. Therefore, setting the numerator equal to zero and solving gives,
1 − 2x − 8x2 = −(8x2 + 2x − 1) = −(4x − 1)(2x + 1) = 0
From this it is pretty easy to see that the derivative will be zero, and hence the function will not be changing, at,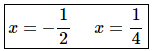
Step 3
To get the answer to this problem all we need to know is where the derivative is positive (and hence the function is increasing) or negative (and hence the function is decreasing). Because the derivative is continuous we know that the only place it can change sign is where the derivative is zero. So, as we did in this section a quick number line will give us the sign of the derivative for the various intervals.
Here is the number line for this problem.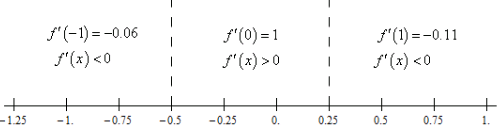
From this we get the following increasing/decreasing information.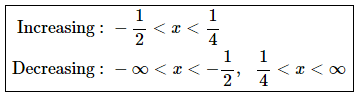
11. Determine where V(t) = (4 − t2) (1 + 5t2) is increasing and decreasing.
Solution:
Step 1
We’ll first need the derivative, for which we will use the product rule, because we know that the derivative will give us the rate of change of the function. Here is the derivative.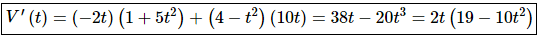
Step 2
Next, we need to know where the function is not changing and so all we need to do is set the derivative equal to zero and solve. From the factored form of the derivative it is easy to see that the derivative will be zero at,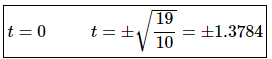
Step 3
To get the answer to this problem all we need to know is where the derivative is positive (and hence the function is increasing) or negative (and hence the function is decreasing). Because the derivative is continuous we know that the only place it can change sign is where the derivative is zero. So, as we did in this section a quick number line will give us the sign of the derivative for the various intervals.
Here is the number line for this problem.
From this we get the following increasing/decreasing information.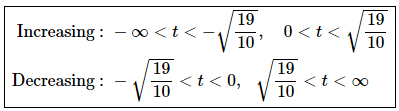
|
112 videos|65 docs|3 tests
|
FAQs on Product and Quotient Rule - Calculus - Mathematics
| 1. What is the Product Rule in mathematics? |  |
| 2. Can you provide an example of using the Product Rule? |  |
| 3. What is the Quotient Rule in mathematics? |  |
| 4. Can you provide an example of using the Quotient Rule? |  |
| 5. How do the Product and Quotient Rules relate to each other? |  |

|
Explore Courses for Mathematics exam
|

|

















