Reduction of Order | Calculus - Mathematics PDF Download
We’re now going to take a brief detour and look at solutions to non-constant coefficient, second order differential equations of the form.
p(t)y′′+q(t)y′+r(t)y=0
In general, finding solutions to these kinds of differential equations can be much more difficult than finding solutions to constant coefficient differential equations. However, if we already know one solution to the differential equation we can use the method that we used in the last section to find a second solution. This method is called reduction of order.
Let’s take a quick look at an example to see how this is done.
Example 1 Find the general solution to
2t2y′′+ty′−3y=0, t>0
given that y1(t)=t−1 is a solution.
Solution:
Reduction of order requires that a solution already be known. Without this known solution we won’t be able to do reduction of order.
Once we have this first solution we will then assume that a second solution will have the form
y2(t)=v(t)y1(t) (1)
for a proper choice of v(t). To determine the proper choice, we plug the guess into the differential equation and get a new differential equation that can be solved for v(t).
So, let’s do that for this problem. Here is the form of the second solution as well as the derivatives that we’ll need.
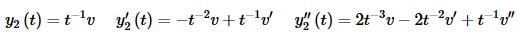
Plugging these into the differential equation gives

Rearranging and simplifying gives
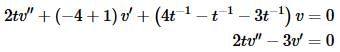
Note that upon simplifying the only terms remaining are those involving the derivatives of v. The term involving v drops out. If you’ve done all of your work correctly this should always happen. Sometimes, as in the repeated roots case, the first derivative term will also drop out.
So, in order for (1) to be a solution then v must satisfy
2tv′′−3v′=0 (2)
This appears to be a problem. In order to find a solution to a second order non-constant coefficient differential equation we need to solve a different second order non-constant coefficient differential equation.
However, this isn’t the problem that it appears to be. Because the term involving the v drops out we can actually solve (2) and we can do it with the knowledge that we already have at this point. We will solve this by making the following change of variable.
w=v′⇒w′=v′′
With this change of variable (2) becomes
2tw′−3w=0
and this is a linear, first order differential equation that we can solve. This also explains the name of this method. We’ve managed to reduce a second order differential equation down to a first order differential equation.
This is a fairly simple first order differential equation so I’ll leave the details of the solving to you. If you need a refresher on solving linear, first order differential equations go back to the second chapter and check out that section. The solution to this differential equation is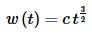
Now, this is not quite what we were after. We are after a solution to (2). However, we can now find this. Recall our change of variable.
v′=w
With this we can easily solve for v(t).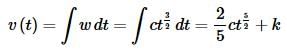
This is the most general possible v(t) that we can use to get a second solution. So, just as we did in the repeated roots section, we can choose the constants to be anything we want so choose them to clear out all the extraneous constants. In this case we can use
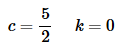
Using these gives the following for v(t) and for the second solution.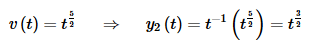
Then general solution will then be,
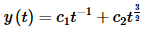
If we had been given initial conditions we could then differentiate, apply the initial conditions and solve for the constants.
Reduction of order, the method used in the previous example can be used to find second solutions to differential equations. However, this does require that we already have a solution and often finding that first solution is a very difficult task and often in the process of finding the first solution you will also get the second solution without needing to resort to reduction of order. So, for those cases when we do have a first solution this is a nice method for getting a second solution.
Let’s do one more example.
Example 2 Find the general solution to
t2y′′+2ty′−2y=0
given that y1(t)=t is a solution.
Solution:
The form for the second solution as well as its derivatives are,
y2(t)=tv y′2(t)=v+tv′ y′′2(t)=2v′+tv′′
Plugging these into the differential equation gives,
t2(2v′+tv′′)+2t(v+tv′)−2(tv)=0=0
Rearranging and simplifying gives the differential equation that we’ll need to solve in order to determine the correct v that we’ll need for the second solution.
t3v′′+4t2v′=0
Next use the variable transformation as we did in the previous example.
w=v′ ⇒w′=v′′
With this change of variable the differential equation becomes
t3w′+4t2w=0
and this is a linear, first order differential equation that we can solve. We’ll leave the details of the solution process to you.
w(t)=ct−4
Now solve for v(t).
v(t)=t−3 ⇒ y2(t)=t(t−3)=t−2
Then general solution will then be,
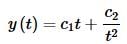
On a side note, both of the differential equations in this section were of the form,
t2y′′+αty′+βy=0
These are called Euler differential equations and are fairly simple to solve directly for both solutions. To see how to solve these directly take a look at the Euler Differential Equation section.
|
112 videos|65 docs|3 tests
|
FAQs on Reduction of Order - Calculus - Mathematics
| 1. What is reduction of order in mathematics? |  |
| 2. How is reduction of order applied in solving differential equations? |  |
| 3. Can reduction of order be used for any type of differential equation? |  |
| 4. What are the limitations of reduction of order? |  |
| 5. Are there any alternative methods to reduction of order for solving differential equations? |  |
















