Problems for Practice - 2 | Algebra - Mathematics PDF Download
For problems 1 – 3 write the given function as a power series and give the interval of convergence.
1. Write the following function as a power series and give the interval of convergence.
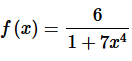
Solution. First, in order to use the formula from this section we know that we need the numerator to be a one. That is easy enough to “fix” up as follows,
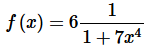
Step 2. Next, we know we need the denominator to be in the form 1−p and again that is easy enough, in this case, to rewrite the denominator to get the following form of the function,
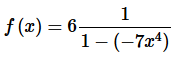
Step 3. At this point we can use the formula from the notes to write this as a power series. Doing this gives,
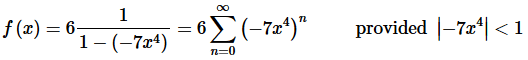
Step 4. Now, recall the basic “rules” for the form of the series answer. We don’t want anything out in front of the series and we want a single x with a single exponent on it.
These are easy enough rules to take care of. All we need to do is move whatever is in front of the series to the inside of the series and use basic exponent rules to take care of the x “rule”. Doing all this gives,
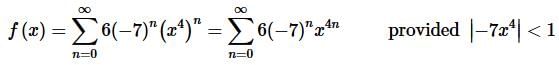
Step 5. To get the interval of convergence all we need to do is do a little work on the “provided” portion of the result from the last step to get,
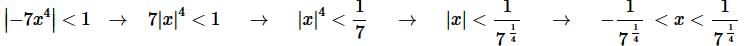
Note that we don’t need to check the endpoints of this interval since we already know that we only get convergence with the strict inequalities and we will get divergence for everything else.
Step 6. The answers for this problem are then,

2. Write the following function as a power series and give the interval of convergence.
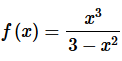
Solution. First, in order to use the formula from this section we know that we need the numerator to be a one. That is easy enough to “fix” up as follows,
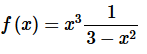
Step 2. Next, we know we need the denominator to be in the form 1−p and again that is easy enough, in this case, to rewrite the denominator by factoring a 3 out of the denominator as follows,
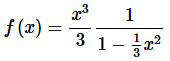
Step 3. At this point we can use the formula from the notes to write this as a power series. Doing this gives,
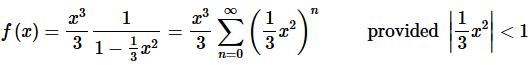
Step 4. Now, recall the basic “rules” for the form of the series answer. We don’t want anything out in front of the series and we want a single x
with a single exponent on it.
These are easy enough rules to take care of. All we need to do is move whatever is in front of the series to the inside of the series and use basic exponent rules to take care of the x
“rule”. Doing all this gives,
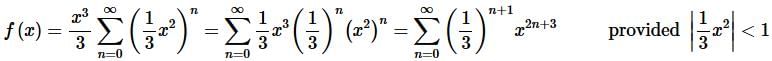
Step 5. To get the interval of convergence all we need to do is do a little work on the “provided” portion of the result from the last step to get,
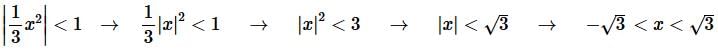
Note that we don’t need to check the endpoints of this interval since we already know that we only get convergence with the strict inequalities and we will get divergence for everything else.
Step 6. The answers for this problem are then,
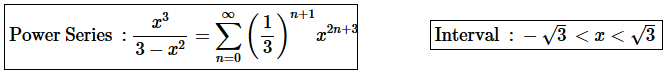
3. Write the following function as a power series and give the interval of convergence.
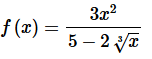
Solution. First, in order to use the formula from this section we know that we need the numerator to be a one. That is easy enough to “fix” up as follows,
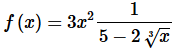
Step 2. Next, we know we need the denominator to be in the form 1−p and again that is easy enough, in this case, to rewrite the denominator by factoring a 5 out of the denominator as follows,
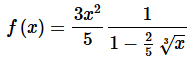
Step 3. At this point we can use the formula from the notes to write this as a power series. Doing this gives,
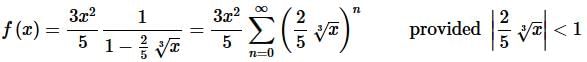
Step 4. Now, recall the basic “rules” for the form of the series answer. We don’t want anything out in front of the series and we want a single x with a single exponent on it.
These are easy enough rules to take care of. All we need to do is move whatever is in front of the series to the inside of the series and use basic exponent rules to take care of the x “rule”. Doing all this gives,
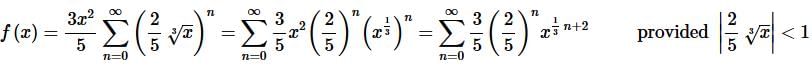
Step 5. To get the interval of convergence all we need to do is do a little work on the “provided” portion of the result from the last step to get,
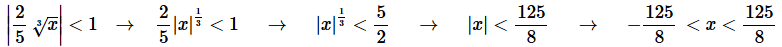
Note that we don’t need to check the endpoints of this interval since we already know that we only get convergence with the strict inequalities and we will get divergence for everything else.
Step 6. The answers for this problem are then,
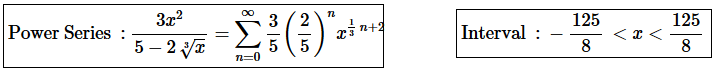
4. Give a power series representation for the derivative of the following function.
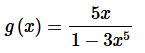
Solution. First let’s notice that we can quickly find a power series representation for this function. Here is that work.
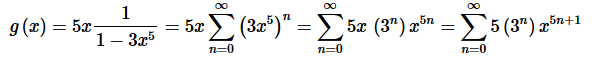
Step 2. Now, we know how to differentiate power series and we know that the derivative of the power series representation of a function is the power series representation of the derivative of the function.
Therefore,
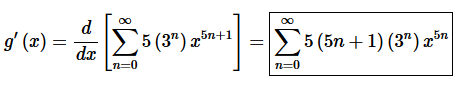
Remember that to differentiate a power series all we need to do is differentiate the term of the power series with respect to x.
5. Give a power series representation for the integral of the following function.
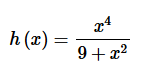
Solution. First let’s notice that we can quickly find a power series representation for this function. Here is that work.
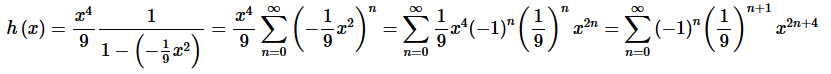
Step 2. Now, we know how to integrate power series and we know that the integral of the power series representation of a function is the power series representation of the integral of the function.
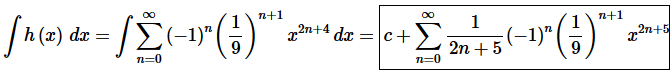
Remember that to integrate a power series all we need to do is integrate the term of the power series and we can’t forget to add on the “+c” since we’re doing an indefinite integral.
|
161 videos|58 docs
|
FAQs on Problems for Practice - 2 - Algebra - Mathematics
| 1. What are the common types of problems in mathematics? |  |
| 2. How can I improve my problem-solving skills in mathematics? |  |
| 3. What are some effective strategies for solving word problems in mathematics? |  |
| 4. How can I overcome math anxiety and perform better in mathematics exams? |  |
| 5. Are there any online resources or websites that can help me practice mathematics problems? |  |

|
Explore Courses for Mathematics exam
|

|

















