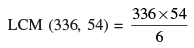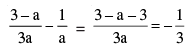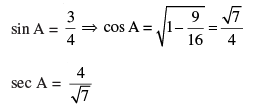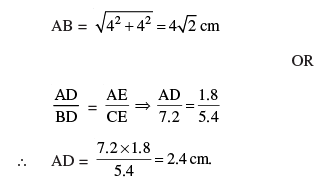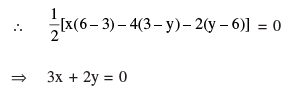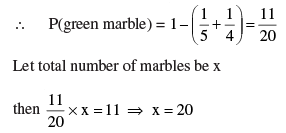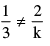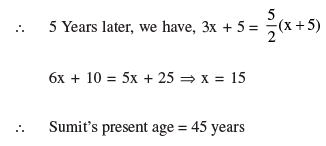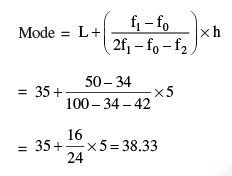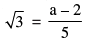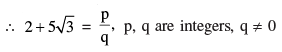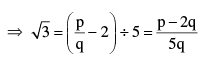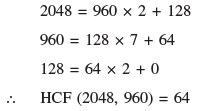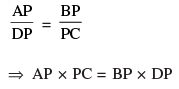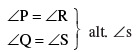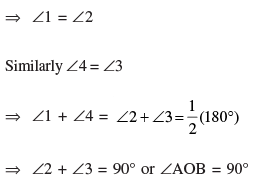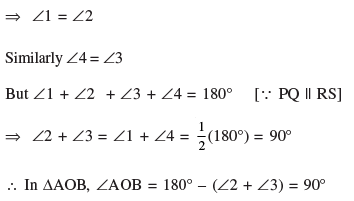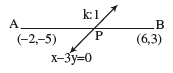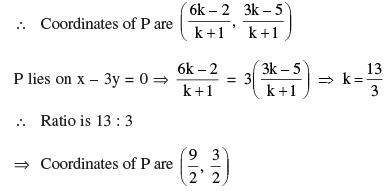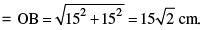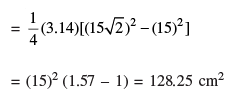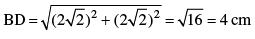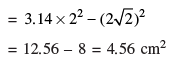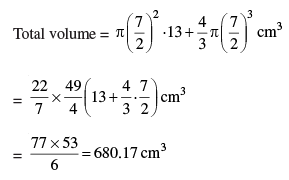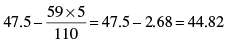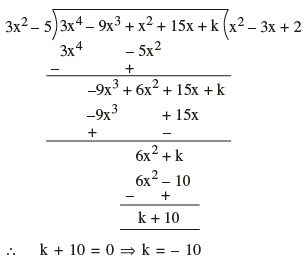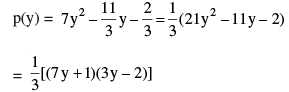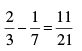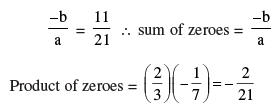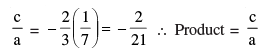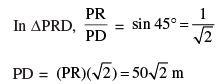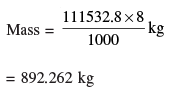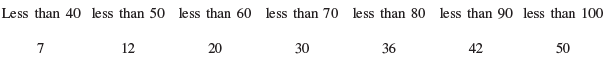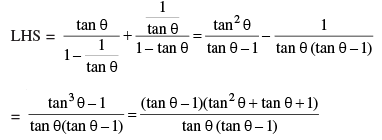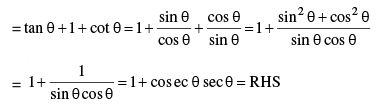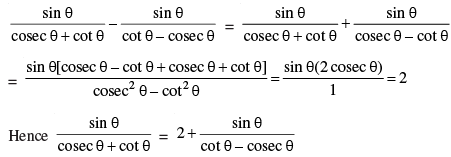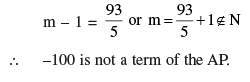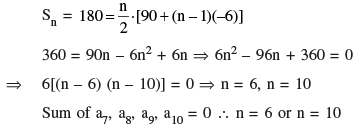Math Past Year Paper with Solution - 2019, Class 10 | Mathematics (Maths) Class 10 PDF Download
Section A
Q 1. If HCF (336, 54) = 6, find LCM (336, 54).
= 336 × 9 = 3024
Q 2. Find the nature of roots of the quadratic equation 2x2 – 4x + 3 = 0.
2x2 – 4x + 3 = 0 ⇒ D = 16 – 24 = –8
∴ Equation has NO real roots
Q 3. Find the common difference of the Arithmetic Progression (A.P.)
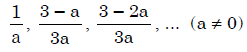
Q 4. Evaluate : sin2 60o + 2 tan 45o – cos2 30o
Or
If sin A = 3/4 , calculate sec A.
sin2 60° + 2 tan 45° – cos2 30
[For any two correct values]
= 2
oR
Q 5. Write the coordinates of a point P on the x-axis which is equidistant from points A(– 2, 0) and B(6, 0).
The point on x-axis is (2, 0)
Q 6. In Figure 1, ABC is an isosceles triangle right angled at C with AC = 4 cm. Find the length of AB.
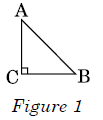
OR
In Figure 2, DE || BC. Find the length of side AD, given that AE = 1·8 cm,
BD = 7·2 cm and CE = 5·4 cm.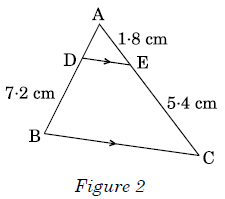
∆ABC: Isosceles ∆ ⇒ AC = BC = 4 cm.
Section B
Q 7. Write the smallest number which is divisible by both 306 and 657.
Smallest number divisible by 306 and 657 = LCM (306, 657)
LCM (306, 657) = 22338
Q 8. Find a relation between x and y if the points A(x, y), B(– 4, 6) and
C(– 2, 3) are collinear.
OR
Find the area of a triangle whose vertices are given as (1, – 1) (– 4, 6) and
(– 3, – 5).
A, B, C are collinear ⇒ ar. (∆ABC) = 0
OR
Q 9. The probability of selecting a blue marble at random from a jar that
contains only blue, black and green marbles is 1/5. The probability of
selecting a black marble at random from the same jar is 1/4. If the jar
contains 11 green marbles, find the total number of marbles in the jar.
P(blue marble) = 1/5 , P(black marble)= 1/4
Q 10. Find the value(s) of k so that the pair of equations x + 2y = 5 and
3x + ky + 15 = 0 has a unique solution.
For unique solution
⇒ k ≠ 6
Q 11. The larger of two supplementary angles exceeds the smaller by 18o. Find
the angles.
OR
Sumit is 3 times as old as his son. Five years later, he shall be two and a half times as old as his son. How old is Sumit at present?
Let larger angle be x°
∴ Smaller angle = 180° – x°∴ (x) – (180 – x) = 18
2x = 180 + 18 = 198 ⇒ x = 99
∴ The two angles are 99°, 81°
OR
Let Son’s present age be x years
Then Sumit’s present age = 3x years.
Q 12. Find the mode of the following frequency distribution :

Maximum frequency = 50, class (modal) = 35 – 40.
Section C
Q 13. Prove that 2 + 5 √3 is an irrational number, given that √3 is an irrational number
OR
Using Euclid’s Algorithm, find the HCF of 2048 and 960.
Let 2+5√3 = a , where ‘a’ is a rational number.
than
Which is a contradiction as LHS is irrational and RHS is rational
∴ 2+5√3 can not be rational
Hence 2+5√3 is irrational.
Alternate method:
Let 2+5√3 be rational
LHS is irrational and RHS is rational
which is a contradiction.∴ 2+5√3 is irrational.
OR
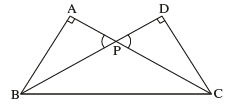
Q 14. Two right triangles ABC and DBC are drawn on the same hypotenuse BC and on the same side of BC. If AC and BD intersect at P, prove that AP x PC = BP x DP.
OR
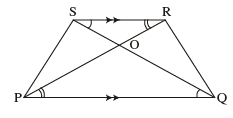
Diagonals of a trapezium PQRS intersect each other at the point O, PQ || RS and PQ = 3RS. Find the ratio of the areas of triangles POQ and ROS.
Correct Figure
∆APB ~ ∆DPC [AA similarity]
OR
Correct Figure
In ∆POQ and ∆ROS∴ ∆POQ ~ ∆ROS [AA similarity]
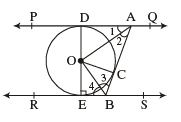
Q 15. In Figure 3, PQ and RS are two parallel tangents to a circle with centre O
and another tangent AB with the point of contact C intersecting PQ at A and
RS at B. Prove that ∠ AOB = 90o.
Correct Figure
∆AOD ≅ AOC [SAS]
Alternate method:
Correct Figure
∆OAD ≅ ∆AOC [SAS]
Q 16. Find the ratio in which the line x – 3y = 0 divides the line segment
joining the points (– 2, – 5) and (6, 3). Find the coordinates of the point of
intersection.
Let the line x – 3y = 0 intersect the segment
joining A(–2, –5) and B(6, 3) in the ratio k : 1
Q 17. Evaluate :
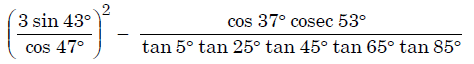
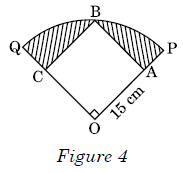
Q 18. In Figure 4, a square OABC is inscribed in a quadrant OPBQ. If OA = 15 cm, find the area of the shaded region. (Use π = 3·14)
OR
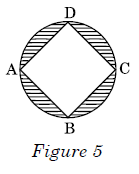
In Figure 5, ABCD is a square with side 2√2 cm and inscribed in a circle. Find the area of the shaded region. (Use π = 3·14)
Radius of quadrant
Shaded area = Area of quadrant – Area of square
OR
∴ Radius of circle = 2 cm
∴ Shaded area = Area of circle – Area of square
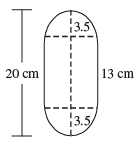
Q 19. A solid is in the form of a cylinder with hemispherical ends. The total
height of the solid is 20 cm and the diameter of the cylinder is 7 cm. Find
the total volume of the solid. (Use π = 22/7)
Height of cylinder = 20 – 7 = 13 cm.
Q 20. The marks obtained by 100 students in an examination are given below :
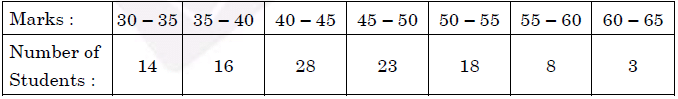
Find the mean marks of the students.
Mean =
Note: If N is taken as 100, Ans. 44.55
Q 21. For what value of k, is the polynomial f(x) = 3x4 – 9x3 + x2 + 15x + k completely divisible by 3x2 – 5 ?
OR
Find the zeroes of the quadratic polynomial  and verify the relationship between the zeroes and the coefficients.
and verify the relationship between the zeroes and the coefficients.
OR
∴ Zeroes are 2/3, –1/7
Sum of zeroes =
Q 22. Write all the values of p for which the quadratic equation x2 + px + 16 = 0 has equal roots. Find the roots of the equation so obtained.
x2 + px + 16 = 0 have equal roots if D = p2 – 4(16)(1) = 0
p2 = 64 ⇒ p = ±8
∴ x2 ± 8x + 16 = 0 ⇒ (x ± 4)2 = 0
x ± 4 = 0∴ Roots are x = –4 and x = 4
Section D
Q 23. If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then prove that the other two sides are divided in the same ratio.
Given: DE ∣∣ BC
To prove that:
EC / AE = BD / ADProof: ∠AED=∠ACB Corresponding angles
∠ADE = ∠ABC Corresponding angles
∠EAD is common to both the triangles
⇒ ΔAED ∼ ΔACB by AAA similarity
⇒ AE / AC = AD / AB
⇒ AE + EC / AE = AD + BD / AD
⇒ EC / AE = BD / AD
Hence proved
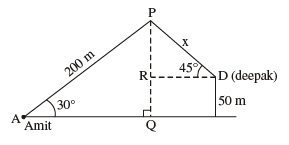
Q 24. Amit, standing on a horizontal plane, finds a bird flying at a distance of 200 m from him at an elevation of 30o. Deepak standing on the roof of a 50 m high building, finds the angle of elevation of the same bird to be 45o. Amit and Deepak are on opposite sides of the bird. Find the distance of the bird from Deepak.
In ∆APQ
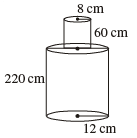
Q 25. A solid iron pole consists of a cylinder of height 220 cm and base diameter 24 cm, which is surmounted by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that 1 cm3 of iron has approximately 8 gm mass. (Use π = 3·14)
Total volume = 3.14 (12)2 (220) + 3.14(8)2(60) cm3
= 99475.2 + 12057.6 = 111532.8 cm3
Q 26. Construct an equilateral ΔABC with each side 5 cm. Then construct another triangle whose sides are 2/3 times the corresponding sides of ΔABC
OR
Draw two concentric circles of radii 2 cm and 5 cm. Take a point P on the outer circle and construct a pair of tangents PA and PB to the smaller circle. Measure PA.
Constructing an equilateral triangle of side 5 cm
Constructing another similar ∆ with scale factor 2/3OR
Constructing two concentric circles of radii 2 cm and 5 cm
Drawing two tangents PA and PB
PA = 4.5 cm (approx)
Q 27. Change the following data into ‘less than type’ distribution and draw its ogive :
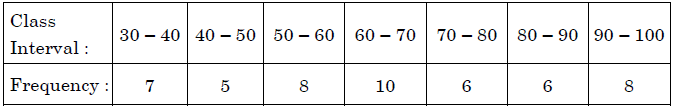
Plotting of points (40, 7), (50, 12), (60, 20), (70, 30), (80, 36), (90, 42) and (100, 50)
Joining the points to get the curve
Q 28. Prove that :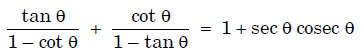
OR
Prove that :
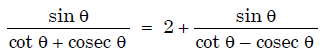
OR
Consider
Q 29. Which term of the Arithmetic Progression –7, –12, –17, –22, ... will be –82? Is –100 any term of the A.P. ? Give a reason for your answer.
OR
How many terms of the Arithmetic Progression 45, 39, 33, ... must be taken so that their sum is 180? Explain the double answer.
Let –82 = an
∴ –82 = –7 + (n – 1) (–5)
⇒ 15 = n – 1 or n = 16
Again –100 = am = –7 + (m – 1) (–5)
⇒ (m – 1)(–5) = –93
OR
Q 30. In a class test, the sum of Arun’s marks in Hindi and English is 30. Had he got 2 marks more in Hindi and 3 marks less in English, the product of the marks would have been 210. Find his marks in the two subjects.
Let marks in Hindi be x
Then marks in Eng = 30 – x
∴ (x + 2) (30 – x – 3) = 210
⇒ x2 – 25x + 156 = 0
or (x – 13) (x – 12) = 0
⇒ x = 13 or x = 12
∴ 30 – 13 = 17 or 30 – 12 = 18
∴ Marks in Hindi & English are
(13, 17) or (12, 18)
|
127 videos|584 docs|79 tests
|
FAQs on Math Past Year Paper with Solution - 2019, Class 10 - Mathematics (Maths) Class 10
| 1. What is the format of the Class 10 Math Past Year Paper with Solution for 2019? |  |
| 2. How many questions are included in each section of the Class 10 Math Past Year Paper with Solution for 2019? |  |
| 3. Are the solutions provided for all the questions in the Class 10 Math Past Year Paper with Solution for 2019? |  |
| 4. Can the Class 10 Math Past Year Paper with Solution for 2019 be used for exam preparation? |  |
| 5. Where can I find the Class 10 Math Past Year Paper with Solution for 2019? |  |