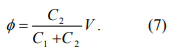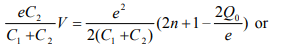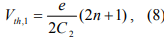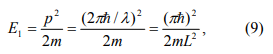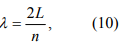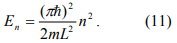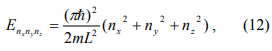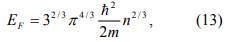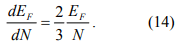Coulomb Blockade and Single Electron Transistors
Another interesting mesoscopic system is a quantum dot (e.g., a conductive or semiconducting grain). When the grain is small enough, the addition or removal of a single electron can cause a change in the electrostatic energy or Coulomb energy that is greater than the thermal energy and can control the electron transport into and out of the grain. This sensitivity to individual electrons has led to electronics based on single electrons. For a really small grain, the discrete energy levels of the electrons in the grain becomes pronounced, like those in atoms and molecules, so one can talk about “artificial atoms and molecules”. Because of the quantum effect, such grain is often referred to as a “quantum dot”. When the wavefunctions between two quantum dots overlap, the coupled quantum dots exhibit the properties of a molecule.
To date, the electron transport properties in a variety of quantum dot systems have been studied. Examples include semiconductor nanostructures fabricated with electron beam lithography (split gate), a metal nanoparticles sandwitched between two electrodes or between a substrate and a STM tip and even electrochemical systems using nanoelectrodes.
Coulomb blockade and staircase
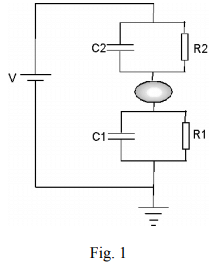
Let us consider a metal nanoparticle sandwiched between two metal electrodes (fig 1). The nanoparticle is separated from the electrodes by vacuum or insulation layer (such as oxide or organic molecules) so that only tunneling is allowed between them. So we can model each of the nanoparticles-electrode junctions with a resistor in parallel with a capacitor. The resistance is determined by the electron tunneling and the capacitance depends on the size of the particle. We denote the resistors and capacitors by R1, R2, C1 and C2, and the applied voltage between the electrodes by V. We will discuss how the current, I, depends on V.
When we start to increase V from zero, no current can flow between the electrodes because move an electron onto (charging) or off (discharging) from an initially neutral nanoparticle cost energy by an amount of
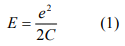
where C is the capacitance of the nanoparticles. This suppression of electron flow is called Coulomb blockade, first observed in the 60s by Giaever at GE in the tunneling junctions that contain metal particles. Current start to flow through the nanoparticles only when the applied voltage V is large enough to establish a voltage ϕ at the nanoparticles such that
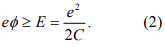
This voltage is called threshold voltage and denoted by Vth. So in the I-V curve, we expect a flat zero-current regime with a width of 2Vth. When the applied voltage reaches Vth, an electron is added to (removed from) the nanoparticles. Further increasing the voltage, the current does not increase proportionally because it requires us to add (or remove) two electrons onto the nanoparticles, which cost a greater amount of energy. Once the applied voltage is large enough to overcome the Coulomb energy of two electrons, the current starts to increase again. This leads to a stepwise increase in I-V curve, called Coulomb staircase. We can now look at the problem in a more quantitative fashion.
First, let us consider the electrostatic energy required to chare a nanoparticle with n electrons. In the absence of applied voltage, V, it is simply given by
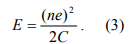
This formula has to be modified for two reasons. First, a nanoparticle in a real experiment is usually electrically polarized by surrounding random charged impurities, polar groups and counter ions. The charge impurity can be modeled by an offset charge”, Q0, in the nanoparticle. Because the “offset charge” is originated from polarization, it can take any value, and hence, is usually not an integer multiple of e. Second, in a real experiment the nanoparticle is coupled with two electrodes and the electrode-nanoparticle-electrode” system is described by two capacitors, C1 and C2 (see fig. 1). Seeing from the nanoparticle, C1 and C2 are in parallel, so the equivalent capacitance is C1+C2 (In the absence of V, no current flows, so R1, R2 and V can be taken out of the circuit in Fig. 1). When both the “offset charge” and coupling with the electrodes are taken into account, Eq. 3 becomes
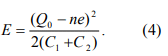
From Eq. 4, we can conclude that in the minimum energy state, n takes an integer value, n0, closest to Q0/e so that
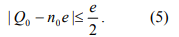
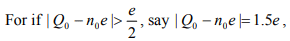 then an electron will transfer onto or from the dot, or
then an electron will transfer onto or from the dot, or 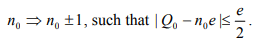
Second, we consider the change in electrostatic energy of the system when an electron is added to the dot. Using Eq. 4, we have
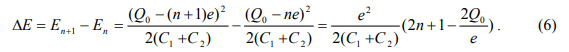
When Q0=n=0, that is when the dot is initially neutral and has no offset charge, the energy change is 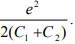 Another interesting special case is when
Another interesting special case is when 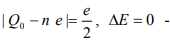 Coulomb blockade! It is thus clear that the offset charge play an important role in the electron transport of the system. In general, we have to applied a large enough voltage in order to overcome the Coulomb blockade and move electrons onto/off the particle. How large voltage is needed is what we want to determine next.
Coulomb blockade! It is thus clear that the offset charge play an important role in the electron transport of the system. In general, we have to applied a large enough voltage in order to overcome the Coulomb blockade and move electrons onto/off the particle. How large voltage is needed is what we want to determine next.
For a given applied bias V, we need first to determine the potential φ with respect to ground at the quantum dot (the voltage across C1). This is a problem of two capacitors in series, and we can easily show that 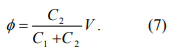
As we increase V, φ increases proportionally. When the associated energy, eφ, equals the charging energy given by Eq. 6, an electron is then added to the nanoparticle, which is described by 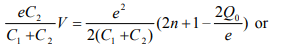
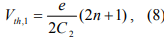
where Vth,1 corresponds to the threshold voltage to move an electron onto the nanoparticle. If n=0 and Q0=0, the threshold voltage for transferring an electron across C1 to the nanoparticle is e/2C2. By the same token, the threshold voltage for transferring an electron across C2 to the nanoparticle is e/2C1. So the observed threshold voltage is the lower of e/2C1 and e/2C2. Coulomb staircase occurs at the threshold voltages for changing the average electron number from n to n+1. According to Eq. 8, the spacing between nth and (n+1)th steps is e/C2 if charging across C1 dominates or e/C1 if charging across C2 dominates.
Quantum confinement effects
The Coulomb blockade effect discussed above is purely due to electrostatic energy of the extra electron on the nanoparticle. However, according to quantum mechanics, confining an electron inside of a nanoparticle costs also kinetic energy. This can be understood by looking at an electron in an infinite deep potential well of width L. The electron form standing waves according to the Schordinger equation. The longest wavelength (λ) of the allowed electron waves is 2L, which gives rise to the lowest energy state 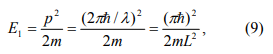
where p = 2πℏ / λ is the momentum of the electron. This is minimum extra energy that an electron must have to be added to the nanoparticle. The electron can have longer wavelength, but it has to satisfy the following condition
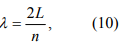
where n=1, 2, 3, …
So the allowed kinetic energy is discrete and given by
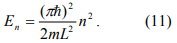
If we model the nanoparticle with a three dimensional cube of edge length L, we can generalize Eq. 11 to
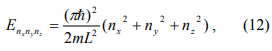
where nx, ny and nz take the values of 1, 2, 3, … When we measure the current I as a function of bias voltage V, the current is initially small (with the exception of Q0=e/2) until V is increased above the Coulomb blockade value. Then an additional resonant tunneling channel opens each time the available energy from the voltage source passes through of the discrete energy levels, which gives rise to new steps in the I-V curves.
We can estimate the width of the steps without using Eq. 12. The Fermi energy EF is
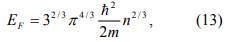
where n is the number of electrons per unit volume. From Eq.13 and n=N/V, we can see that
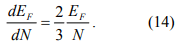
So the spacing between the discrete levels is roughly the Fermi energy divided by the number of electrons (atoms for monovalent metal) in the nanoparticle.

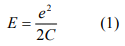
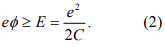
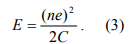
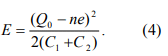
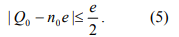
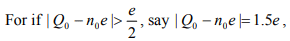 then an electron will transfer onto or from the dot, or
then an electron will transfer onto or from the dot, or 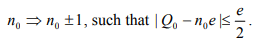
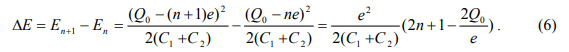
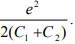 Another interesting special case is when
Another interesting special case is when 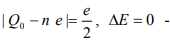 Coulomb blockade! It is thus clear that the offset charge play an important role in the electron transport of the system. In general, we have to applied a large enough voltage in order to overcome the Coulomb blockade and move electrons onto/off the particle. How large voltage is needed is what we want to determine next.
Coulomb blockade! It is thus clear that the offset charge play an important role in the electron transport of the system. In general, we have to applied a large enough voltage in order to overcome the Coulomb blockade and move electrons onto/off the particle. How large voltage is needed is what we want to determine next.