Past Year Questions: Highway Geometric Design & Planning - 1 | Transportation Engineering - Civil Engineering (CE) PDF Download
Q1: A vertical summit curve on a freight corridor is formed at the intersection of two gradients, +3.0% and −5.0%.
Assume the following: [2024 ,Set -2]
Only large-sized trucks are allowed on this corridor.
Design speed =80kmph
Eye height of truck drivers above the road surface = 2.30 m
Height of object above the road surface for which trucks need to stop = 0.35 m
Total reaction time of the truck drivers = 2.0 s
Coefficient of longitudinal friction of the road = 0.36
Stopping sight distance gets compensateon the gradient.
The design length of the summit curve (in meters) to accommodate the stopping sight distance is _____ (rounded off to 2 decimal places).
Ans: Range: 117 to 120
Sol: 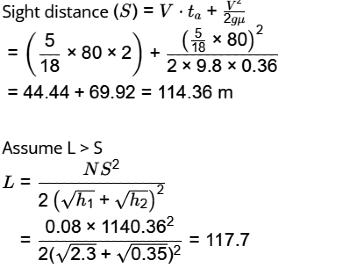
Q2: In general, the outer edge is raised above the inner edge in horizontal curves for [2024, Set-2]
(a) Highways, Railways, and Taxiways
(b) Highways and Railways only
(c) Railways and Taxiways only
(d) Highways only
Ans: (b)
Q3: A car is travelling at a speed of 60 km/hr on a section of a National Highway having a downward gradient of 2% . The driver of the car suddenly observes a stopped vehicle on the car path at a distance 130 m ahead, and applies brake. If the brake efficiency is 60% , coefficient of friction is 0.7 , driver's reaction time is 2.5 s. and acceleration due to gravity is 9.81 m/s2, the distance (in meters) required by the driver to bring the car to a safe stop lies in the range [2024, Set -1]
(a) 126 to 130
(b) 41 to 45
(c) 33 to 37
(d) 75 to 79
Ans: (d)
Sol:
Given,
V = 60 km/hr, tR 2.5sec
Braking efficiency, η = 60 %
Coefficient of friction, μ = 0.7 %
Down grace, s = 2 %
Stopping sight distance = Lag distance + Braking distance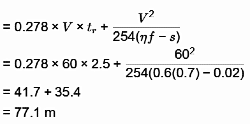
Q1: As per the Indian Roads Congress guidelines (IRC 86: 2018), extra widening depends on which of the following parameters? [2023, Set-2]
(a) Horizontal curve radius
(b) Superelevation
(c) Number of lanes
(d) Longitudinal gradient
Ans: (a, c)
Sol: As per IRC 86:2018
Clause 8.6 Widening of Carriageway on Curves:
At sharp horizontal curves, it is necessary to widen the carriageway to provide for safe passage of vehicles. The widening required has two components: (i) mechanical widening to components for the extra width occupied by a vehicle on the curve due to tracking of the rare wheels, and (ii) psychological widening to permit easy crossing of vehicles since vehicles in a lane tend to wander more on a curve than on a straight reach.
On two-lane or wider roads, it is necessary that both the above components should be fully catered for so that the lateral clearance between vehicles of curves is maintained equal to the clearance available on straight. Position of single-lane roads however is somewhat different.
Since during crossing maneuvers outer wheels of vehicles have in any case to use the shoulder whether on the straight or on the curve. It is, therefore sufficient on single lane roads if only the mechanical component of widening is taken into account.
Based on the above considerations, the extra width of carriageway to be provided at horizontal curves on single and two-lane roads is given in Table For multi-lane roads, the pavement widening may be calculated by adding half the widening for two-lane roads to each lane.
Table : Extra width of Pavement at Horizontal Curves
Q2: Which of the following is equal to the stopping sight distance? [2023, Set-2)
(a) (braking distance required to come to stop) + (distance travelled during the perception- reaction time)
(b) (braking distance required to come to stop) - (distance travelled during the perception- reaction time)
(c) (braking distance required to come to stop)
(d) (distance travelled during the perception- reaction time)
Ans: (a)
Sol: SSD = Braking distance + lag distance
where,
Braking distance = Braking distance required to come to stop
Lag distance = distance travelled during the perception reaction time.
Q3: For a horizontal curve, the radius of a circular curve is obtained as 300 m with the design speed as 15 m/s. If the allowable jerk is 0.75 m/s 3, what is the minimum length (in m, in integer) of the transition curve ? [2023, Set-1]
Ans: 15 To 15
Radius of circular curve ( R ) = 300 m
Vd =15 m/s
Allowable jerk ( C ) = 0.75 m / sec3
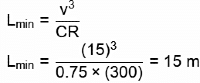
∴ Minimum length of transition curve =15m.
Q4: G1 and G2are the slopes of the approach and departure grades of a vertical curve, respectively. [2023, Set-1]
Given ∣ G1 ∣ < ∣ G2 ∣ and ∣ G1 ∣ ≡ ∣ G2 ∣ ≡ 0
Statement 1: + G1 followed by + G2 results in a sag vertical curve.
Statement 2: − G1 followed by − G2 results in a sag vertical curve.
Statement 3: + G1 followed by - G2 results in a crest vertical curve.
Which option amongst the following is true?
(a) Statement 1 and Statement 3 are correct; Statement 2 is wrong
(b) Statement 1 and Statement 2 are correct; Statement 3 is wrong(c) Statement 1 is correct; Statement 2 and Statement 3 are wrong
(d) Statement 2 is correct; Statement 1 and Statement 3 are wrong
Ans: (a)
Sol: Given ∣ G1 ∣ < ∣ G2 ∣ and ∣ G1 ∣ ≡ ∣ G2 ∣ ≡ 0
Statement 1:
∣ G1 ∣ < ∣ G2 ∣
This results in a vertical sag curve.
Statement 2:
∣ G1 ∣ < ∣ G2 ∣
This results in a vertical crest curve.
Statement 3: 
∣ G1 ∣ < ∣ G2 ∣
This results in a vertical crest curve.
Q1: A parabolic vertical crest curve connects two road segments with grades +1.0% and -2.0%. If a 200 m stopping sight distance is needed for a driver at a height of 1.2 m to avoid an obstacle of height 0.15 m, then the minimum curve length should be ______ m. (round off to the nearest integer) [2022 Set-2]
Ans: 270 to 275
Sol: Given that, n1 = +1=+1 and n2 = −2
n = n1 -n2 = 3
SSD = 200 m
and h1 = 1.2 m h2 = 0.15 m
as given n1 up gradient, and n2 - down gradient.
So curve is summit curve.
Assume L > SSD
Q2: The base length of the runway at the mean sea level (MSL) is 1500 m. If the runway is located at an altitude of 300 m above the MSL, the actual length (in m) of the runway to be provided is ____________. (round off to the nearest integer) [2022 Set-2]
Ans: 1602 to 1606
Sol: Correction for elevation = It should increase at a rate of 7% per 300 m rise in elevation from MSL.
Given that
Basic runway length as MSL =1500m
Elevation =300m
Correction = 7/100 x 300/300 x 1500 =105m
The actual length of runway= 1500+150=1605m
Q3: The vehicle count obtained in every 10 minute interval of a traffic volume survey done in peak one hour is given below. [2022, Set-1]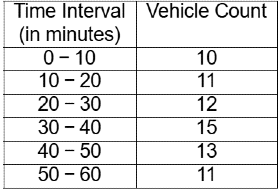
The peak hour factor (PHF) for 10 minute sub-interval is __________. (round off to one decimal place)
Ans: 0.8 to 0.8
Sol: 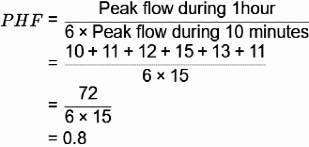
Q4: A horizontal curve is to be designed in a region with limited space. Which of the following measure(s) can be used to decrease the radius of curvature? [2022, Set-1]
(a) Decrease the design speed.
(b) Increase the superelevation.
(c) Increase the design speed.
(d) Restrict vehicles with higher weight from using the facility.
Ans: (a, b)
Sol:
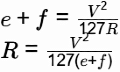
Q1: The stopping sight distance (SSD) for a level highway is 140 m for the design speed of 90 km/h. The acceleration due to gravity and deceleration rate are 9.81 m/s2 and 3.5 m/s2 , respectively. The perception/reaction time (in s, round off to two decimal places) used in the SSD calculation is ______________ [2021, Set-2]
Ans: 1.9 to 2.1
Sol: SSD = 14m
V =90kmph
a = 3.5 m/s2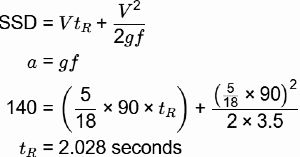
Q2: On a road, the speed - density relationship of a traffic stream is given by u=70 - 0.7k (where speed, u, is in km/h and density, k is in veh/km). At the capacity condition, the average time headway will be [2021, Set-1]
(a) 0.5s
(b) 1.0s
(c) 1.6s
(d) 2.1s
Ans: (d)
Sol: 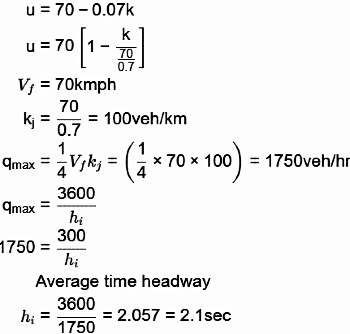
Q3: A highway designed for 80 km/h speed has a horizontal curve section with radius 250 m. If the design lateral friction is assumed to develop fully, the required super elevation is [2021, Set-1]
(a) 0.02
(b) 0.05
(c) 0.07
(d) 0.09
Ans: (b)
Sol: V = 80kmph, R =250 m
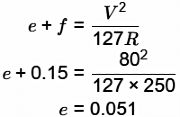
Q4: The shape of the most commonly designed highway vertical curve is [2021, Set-1]
(a) circular (single radius)
(b) circular (multiple radii)
(c) parabolic
(d) spiral
Ans: (c)
Sol: The ideal vertical curve is a 2∘ parabola.
Q1: The design speed of a two-lane two-way road is 60 km/h and the longitudinal coefficient of friction is 0.36. The reaction time of a driver is 2.5 seconds. Consider acceleration due to gravity as 9.8 m/ 2. The intermediate sight distance (in m, round off to the nearest integer) required for the load is ________ [2020, Set-2]
Ans: 154 to 178
Sol: Give: f = 0.36; v = 60 km; g = 9.8 m/s2 ; t R = 2.5S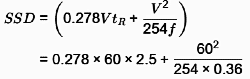
= 41.7 + 39.37 = 81 m
ISD = 2 x SSD
= 81 x 2 = 162m
Q2: In an urban area, a median is provided to separate the opposing streams of traffic. As per IRC : 86-1983, the desirable minimum width (in m, expressed as integer) of the median, is __________. [2020, Set-1]
Ans: 5 to 5
Sol: As per IRC : 86-1983
Desirable minimum width of median in urban roads = 5 m
Q1: The coefficient of average rolling friction of a road is fr and its grade is +G%. If the grade of this road is doubled, what will be the percentage change in the braking distance (for the design vehicle to come to a stop) measured along the horizontal (assume all other parameters are kept unchanged)? [2019, Set-1]
(a) 0.01G/fr + 0.02G x 100
(b) fr /fr + 0.02G x 100
(c) 0.02G/fr + 0.01G x 100
(d) 2 fr/fr + 0.01G x 100
Ans: (a)
Sol: Percentage change in Braking Distance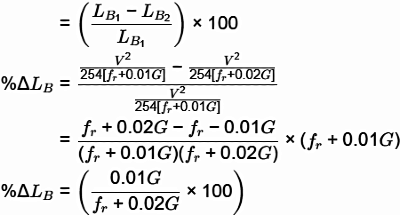
Q1: A 7.5 m wide two-lane road on a plain terrain is to be laid along a horizontal curve of radius 510 m. For a design speed of 100 kmph, super-elevation is provided as per IRC: 73-1980. Consider acceleration due to gravity as 9.81 m/s2 . The level difference between the inner and outer edges of the road (in m, up to three decimal places) is _____ [2018, Set-2]
Ans: 0.52 to 0.53
Sol:
 = 0 .0871 x 0.07 = tan θ
= 0 .0871 x 0.07 = tan θ
sin θ ≃ 0.07
x = 7.5 x sin θ = 0.525m
Q2: A car follows a slow moving truck (travelling at a speed of 10 m/s) on a two-lane two-way highway. The car reduces its speed to 10 m/s and follows the truck maintaining a distance of 16 m from the truck. On finding a clear gap in the opposing traffic stream, the car accelerates at an average rate of 4 m/s2, overtakes the truck and returns to its original lane. When it returns to its original lane, the distance between the car and the truck is 16 m. The total distance covered by the car during this period (from the time it leaves its lane and subsequently returns to its lane after overtaking) is [2018, Set-2]
(a) 64m
(b) 72m
(c) 128m
(d) 144m
Ans: (b)
Sol: Overtaking time, S= Space heady way =16m
S= Space heady way =16m
a= Acceleration =4m/s2
Distance travelled by vehicle = S2
Q3: A priority intersection has a single-lane one-way traffic road crossing an undivided two-lane two-way traffic road. The traffic stream speed on the single-lane road is 20 kmph and the speed on the two-lane road is 50 kmph. The perception-reaction time is 2.5s, coefficient of longitudinal friction is 0.38 and acceleration due to gravity is 9.81 m/s2 . A clear sight triangle has to be ensured at this intersection. The minimum lengths of the sides of the sight triangle along the two-lane road and the single-lane road, respectively will be [2018, Set-1]
(a) 50 m and 20 m
(b) 61 m and 18 m
(c) 111 m and 15 m
(d) 122 m and 36 m
Ans: (c)
Sol: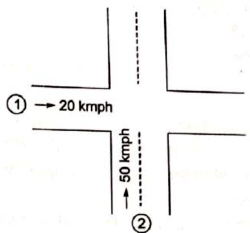
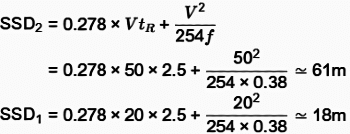
As per data given and based on calculation of SSD the answer would be 61 m and 18 m.
But, as per the code IRC : 66 of sight distance calculation at priority intersection, the sight triangle at priority intersection should be formed by measuring a distance of 15 m along minor road and a distance equal to 8 seconds travel at the design speed
(50 × 0.278 × 8 ≃ 111m) along major road. Hence answer will be 111 m and 15 m.
Q2: A 7.5 m wide two-lane road on a plain terrain is to be laid along a horizontal curve of radius 510 m. For a design speed of 100 kmph, superelevation is provided as per IRC: 73-1980. Consider acceleration due to gravity as 9.81 m/s2. The level difference between the inner and outer edges of the road (in m, up to three decimal places) is _______. [2018, Set-2]
Sol:

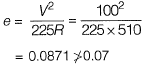
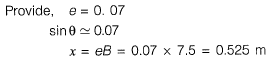
Question 6. While aligning a hill road with a ruling gradient of 6%, a horizontal curve of radius 50 m is encountered. The grade compensation (in percentage, up to two decimal places) to be provided for this case would be __________ . [2017 : 1 Mark, Set-II]
Solution:

∴ Grade compensation = 1.5%
Question 7. The radius of a horizontal circular curve on a highway is 120 m. The design speed is 60 km/ hour, and the design coefficient of lateral friction between the tyre and the road surface is 0.15. The estimated value of superelevation required (if full lateral friction is assumed to develop), and the value of coefficient of friction needed (if no superelevation is provided) will, respectively, be [2017 : 2 Marks, Set-I]
(a) 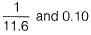
(b) 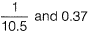
(c) 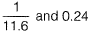
(d) 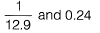
Answer: (c)
Given, R = 120 m, V = 60 kmph and f = 0.15

Question 8. A super-elevation e is provided on a circular horizontal curve such that a vehicle can be stopped on the curve without sliding. Assuming a design speed v and maximum coefficient of side friction fmax, which one of the following criteria should be satisfied? [2017 : 1 Mark, Set-I]
(a) e ≤ fmax
(b) e > fmax
(c) no limit on e can be set
(d) 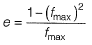
Answer: (a)
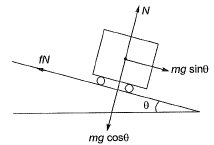
Sliding of stopped vehicle occurs if,
mg sinθ > fn
mg sinθ > f(mg cosθ)
tanθ > f
e> f
Hence, to prevent sliding e ≤ fmax
Question 9. A motorist traveling at 100 km/h on a highway needs to take the next exit, which has a speed limit of 50 km/h. The section of the roadway before the ramp entry has a downgrade of 3% and coefficient of friction (f) is 0.35. In order to enter the ramp at the maximum allowable speed limit, the braking distance (expressed in m) from the exit ramp is_______. [2016 : 2 Marks, Set-II]
Solution: 
Total energy lost between point (1) and (2)
= Work done by frictional force
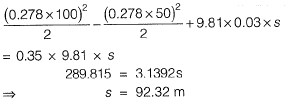
Question 10. A two lane, one-way road with radius of 50 m is predominantly carrying lorries with wheelbase of 5 m. The speed of lorries is restricted to be between 60 kmph and 80 kmph. The mechanical widening and psychological widening required at 60 kmph are designated as Wme 60 and Wps 60, respectively. The mechanical widening and psychological widening required at 80 kmph are designated as Wme 80 and Wps 80, respectively. The correct values of Wme 60, Wps 60, Wme 80, Wps 80, respectively are [2016 : 2 Marks, Set-I]
(a) 0.89 m, 0.50 m, 1.19 m, and 0.50 m
(b) 0.50 m, 0.89 m, 0.50 m, and 1.19 m
(c) 0.50 m, 1.19 m, 0.50 m, and 0.89 m
(d) 1.19 m, 0.50 m, 0.89 m, and 0.50 m
Answer: (b)
Solution:
Method-I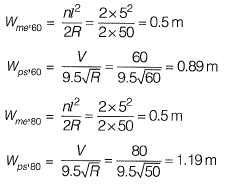
Method-II
As mechanical widening is independent of speed of the vehicle,
Wmc’60= Wme,80
Hence, options (a) and (b) are eliminated.
Now, as psychological widening is directly proportional to the speed of the vehicle.
Wps,60 < Wps,80 Hence, option (b) is the correct answer.
Question. 11 A superspeedway in New Delhi has among the highest super-elevation rates of any track on the Indian Grand Prix circuit. The track requires drivers to negotiate turns with a radius of 335 m and 33° banking. Given this information, the coefficient of side friction required in order to allow a vehicle to travel at 320 km/h along the curve is [2015 : 1 Mark, Set-II]
(a) 1.761
(b) 0.176
(c) 0.253
(d) 2.530
Answer: (a)
Solution: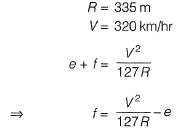
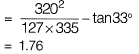
Note: While deriving the above equation, we consider 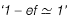 but this is not valid in this case because banking provided is very high (tan 33° = 0.65). So formula used should be
but this is not valid in this case because banking provided is very high (tan 33° = 0.65). So formula used should be
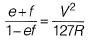 which will result in f = 0.685.
which will result in f = 0.685.
|
27 videos|118 docs|58 tests
|
FAQs on Past Year Questions: Highway Geometric Design & Planning - 1 - Transportation Engineering - Civil Engineering (CE)
| 1. What are the key components of highway geometric design? |  |
| 2. How does lane width affect highway safety and capacity? |  |
| 3. What factors should be considered when planning a new highway? |  |
| 4. What is the role of superelevation in highway design? |  |
| 5. How can sight distance be optimized in highway design? |  |

















