Past Year Questions: Compass & Traverse Surveying | Topic wise GATE Past Year Papers for Civil Engineering - Civil Engineering (CE) PDF Download
Q1: A child walks on a level surface from point P to point Q at a bearing of 30∘ , from point Q to point R at a bearing of 90∘ and then directly returns to the starting point P at a bearing of 240∘. The straightline paths PQ and QR are 4m each. Assuming that all bearings are measured from the magnetic north in degrees, the straight-line path length RP (in meters) is ____(rounded off to the nearest integer) [2024, Set-II]
Ans: 6 to 8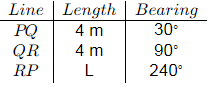
Closed traverse,
ΣL = 0, 4 cos 30∘ + 4 cos 90∘ + L cos 240∘
∴ L = 6.928 m ≈ 7 m
Q2: To finalize the direction of a survey, four surveyors set up a theodolite at a station P and performed all the temporary adjustments. From the station P, each of the surveyors observed the bearing to a tower located at station Q with the same instrument without shifting it. The bearing observed by the surveyors are 30º 30′ 00′′ , 30º 29′ 40′′ , 30º30′20′′ and 30º 3′20′′ . Assuming that each measurement is taken with equal precision, the most probable value of the bearing is [2024, Set-II]
(a) 30º 31′ 20′′
(b) 30º 30′ 00′′
(c) 30º 30′ 20′′
(d) 30º 29′ 40′′
Ans: (c)
Most probable value with equal weightage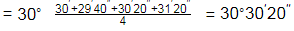
Q3: Among the following statements relating the fundamental lines of a transit theodolite, which one is CORRECT [2024, Set-I]
(a) The Vernier of vertical circle must read zero when the line of collimation is vertical.
(b) The axis of plate level must lie in a plane parallel to the vertical axis.
(c) The axis of altitude level must be perpendicular to the line of collimation
(d) The line of collimation must be perpendicular to the horizontal axis at its intersection with the vertical axis.
Ans: (d)
Line of collimation must be perpendicular to horizontal axis.
Q4: A surveyor observes a zenith angle of 93∘ 00′ 00′′ during a theodolite survey The corresponding vertical angle is [2024, Set-I]
(a) +87º 00′ 00′′
(b) −87º 00′ 00′′
(c) +03º 00′ 00′′
(d) −03º 00′ 00′′
Ans: (d)
Zenith = 93∘ 00′ 00′′
Q5: If the number of sides resulting in a closed traverse is increased from three to four, the sum of the interior angles increases by [2024, Set-I]
(a) 360º
(b) 270º
(c) 90º
(d) 180º
Ans: (d)
Sum of interior angles = (n − 2) × 180º
So, sum of interior angles for 3 sides = (3 − 2) × 180∘ = 180º
Now, sum of interior angles for 4 sides = (4 − 2) × 180∘ = 360∘
∴ Increase in sum of interior angles = 360∘ − 180∘ = 180∘
Q6: If the magnetic bearing of the Sun at a place at noon is S2º E, the magnetic declination (in degrees) at that place is [2022, Set-II]
(a) 2ºE
(b) 2ºW
(c) 4ºE
(d) 4ºW
Ans: (a)
MB = S2∘E = 180∘ − 2∘= 178
TB = 180∘
Declination,δ = TB − MB = 180 − 178 = 2∘ or 2∘E
Q7: The bearing of a survey line is N31∘ 17′ W. Its azimuth observed from north is ______ deg. (round off to two decimal places) [2022, Set-I]
(a) 328.71
(b) 458.25
(c) 124.65
(d) 625.25
Ans: (a)
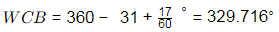
Q8: For a given traverse, latitudes and departures are calculated and it is found that sum of latitudes is equal to +2.1 m and the sum of departures is equal to -2.8 m. The length and bearing of the closing error, respectively, are [2021, Set-II]
(a) 3.50 m and 53∘7′ 48 ′′ NW
(b) 2.45 m and 53∘7′ 48 ′′ NW
(c) 0.35 m and 53.13∘ SE
(d) 3.50 m and 53.13∘ SE
Ans: (a)
Bearing of closing error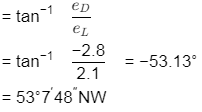
Q9: A horizontal angle θ is measured by four different surveyors multiple times and the values reported are given below.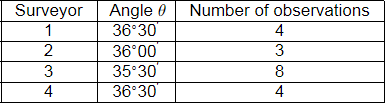 he most probable value of the angle θ (in degree, round off to two decimal placesis ________ [2021, Set-II]
he most probable value of the angle θ (in degree, round off to two decimal placesis ________ [2021, Set-II]
(a) 12
(b) 28
(c) 36
(d) 44
Ans: (c)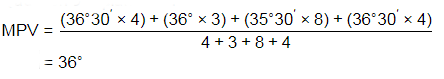
Q10: Traversing is carried out for a closed traverse PQRS. The internal angles at vertices P, Q, R and S are measured as 92∘, 68∘, 123∘ and 77∘ , respectively. If fore bearing of line PQ is 27∘, fore bearing of line RS (in degrees, in integer) is _________ [2021, Set-I]
(a) 258
(b) 196
(c) 159
(d) 218
Ans: (b,d)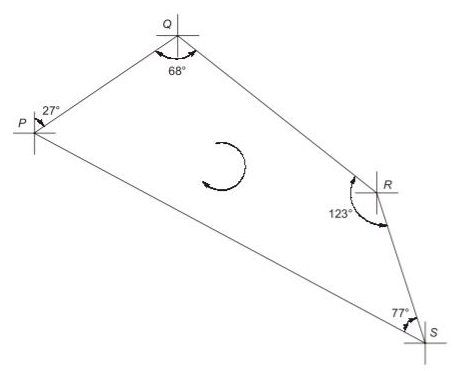
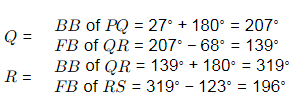
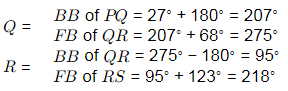
Q11: A theodolite is set up at station A. The RL of instrument axis is 212.250 m. The angle of elevation to the top of a 4 m long staff, held vertical at station B, is 7∘. The horizontal distance between station A and B is 400 m. Neglecting the errors due to curvature of earth and refraction, the RL (in m, round off to three decimal places) of station B is __________ [2020, Set-II]
(a) 257.363
(b) 145.126
(c) 472.156
(d) 324.422
Ans: (a)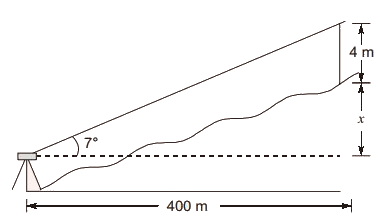
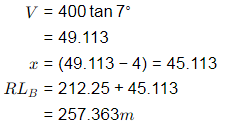
Q12: A theodolite was set up at a station P. The angle of depression to a vane 2 m above the foot of a staff held at another station Q was 45∘. The horizontal distance between stations P and Q is 20 m. The staff reading at a benchmark S of RL 433.050 m is 2.905 m. Neglecting the errors due to curvature and refraction, the RL of the station Q (in m), is [2020, Set-II]
(a) 413.05
(b) 413.955
(c) 431.05
(d) 435.955
Ans: (b) 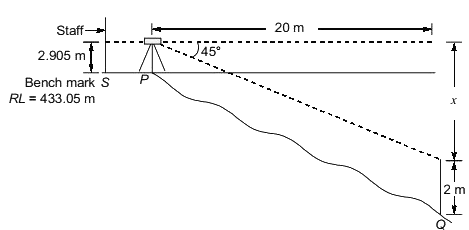
x/20 = tan 45º
x = 20m
Q13: The length and bearings of a traverse PQRS are: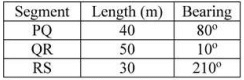 The length of line segment SP (in m, round off to two decimal places), is ________. [2020, Set-I]
The length of line segment SP (in m, round off to two decimal places), is ________. [2020, Set-I]
(a) 33.07
(b) 25.36
(c) 47.78
(d) 44.79
Ans: (d)
ΔL= 40 cos 80∘ + 50 cos 10∘ + 30 cos 210∘
= 30.20
ΔD = 40 sin 80∘ + 50 sin 10∘ + 30 sin 210∘
= 33.07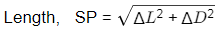
= 44. 79m
Q14: An open traverse PQRST is surveyed using theodolite and the consecutive coordinates obtained are given in the table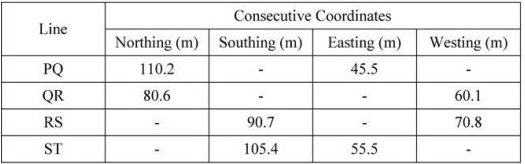 If the independent coordinates (Northing, Easting) of station P are (400 m, 200 m) the independent coordinates (in m) of station T, are [2020, Set-I]
If the independent coordinates (Northing, Easting) of station P are (400 m, 200 m) the independent coordinates (in m) of station T, are [2020, Set-I]
(a) 194.7, 370.1
(b) 205.3, 429.9
(c) 394.7, 170.1
(d) 405.3, 229.9
Ans: (c) 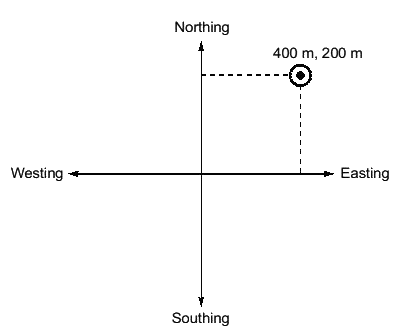 ΔL = −5.3
ΔL = −5.3
ΔD = −29.9
T, Northing {400 + (−5.3)} = 394.7
T, Easting{200 + (−29.9)} = 170.1
T[394.7m, 170.1m]
Q15: The data from a closed traverse survey PQRS (run in the clockwise direction) are given in the table The closing error for the traverse PQRS (in degrees) is ________. [2019 : 1 Mark, Set-II]
The closing error for the traverse PQRS (in degrees) is ________. [2019 : 1 Mark, Set-II]
Ans: Assuming it as anticlockwise traverse. Mathematically sum of interior angle for a closed traverse
= (2n - 4) x 90
= (2 x 4 - 4) x 90
= 4 x 90 = 360°
Given sum of interior angles, = 88 + 92 + 94 + 89 = 363°
Then error in interior angle = 363 - 360 = 3°
Note: In this question as per clockwise traverse included angle should be taken as exterior angle. But if we take exterior angle then we get all interior angles more than 180°.
Q16: The interior angles of four triangles are given below: Which of the triangles are ill-conditioned and should be avoided in Triangulation surveys? [2019 : 1 Mark, Set-I]
Which of the triangles are ill-conditioned and should be avoided in Triangulation surveys? [2019 : 1 Mark, Set-I]
(a) Both Q and S
(b) Both P and S
(c) Both Q and R
(d) Both P and R
Ans: (a)
For a well conditioned triangle.
The interior angle should not be less than 30°. In this way, triangle ‘Q’ & S having less angles (acute angle).
⇒ Q & S are ill-conditioned.
Q17: The following details refer to a closed traverse: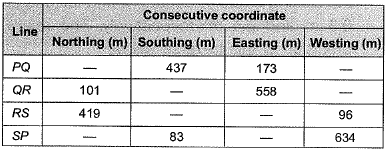
The length and direction (whole circle bearing) of closure, respectively are [2018 : 2 Marks, Set-I]
(a) 1 m and 90°
(b) 2 m and 90°
(c) 1 m and 270°
(d) 2 m and 270°
Ans: (a)
∑L = W northing- E southing
= (101 + 419) - (437 + 83)
= 0
∑D = E Easting - E Westing
= (173 + 558) - (96 + 634)
= 1 m
∴ Length of closure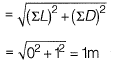
And, direction of closure,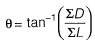
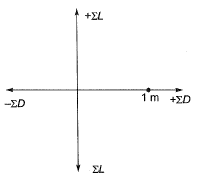
Hence, θ lies in I quadrant and θ = 90°
Q18: The observed bearings of a traverse are given below The station(s) most likely to be affected by the local attraction is/are [2017 : 2 Marks, Set-I]
The station(s) most likely to be affected by the local attraction is/are [2017 : 2 Marks, Set-I]
(a) Only R
(b) Only S
(c) Rand S
(d) Pand Q
Ans: (a)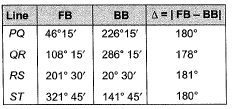 Station R is most likely to be affected.
Station R is most likely to be affected.
Since difference of FB and BB for PQ and ST is 180°.
Hence, P, Q, S, T are free from local attraction.
Q19: The reduced bearing of a 10 m long line is N30°E. The departure of the line is [2016 : 1 Mark, Set-II]
(a) 10.00 m
(b) 8.66 m
(c) 7.52 m
(d) 5.00 m
Ans: (d)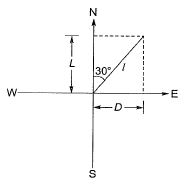 The departure of the line,
The departure of the line,
D = l sin θ
= 10 sin 30°
= 10/2 = 5m
Q20: The bearings of two inaccessible stations, S1 (Easting 500 m, Northing 500 m) and S2 (Easting 600 m, Northing 450 m) from a station S3 were observed as 225° and 153° 26' respectively. The independent Easting (in m) of station S3 is: [2015 : 2 Marks, Set-II]
(a) 450.000
(b) 570.710
(c) 550.000
(d) 650.000
Ans: (c)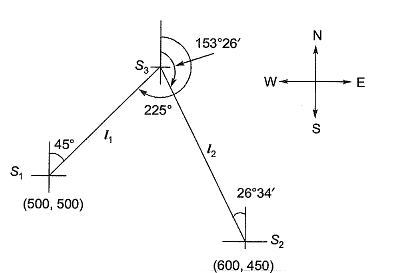 Let S1S3 = l1 and S2S3 = l2
Let S1S3 = l1 and S2S3 = l2
Northing of S3:
500 + l1cos45°= 450 + l2cos26°34'
l1 cos 45° - l2cos 26° 34' = - 50 ..(i)
Easting of S3:
500 + l1 sin 45° = 600 - l2sin26°34'
l1sin45° + l2sin26°34' = 100 ..(ii)
Solving eq. (i) and eq. (ii),
l1 = 70.707
l2 = 111.802
∴ Easting of S3 = 500 + 70.707 sin45°
= 550m
Q21: In a region with magnetic declination of 2°E, the magnetic Fore Bearing (FB) of a line AB was measured as N79°50'E. There was local attraction at A. To determine the correct magnetic bearing of the line, a point 0 was selected at which there was no local attraction. The magnetic FB of line AO and OA were observed to be S52°40'E and N50°20'W, respectively. What is the true FB of line AB? [2015 : 2 Marks, Set-I]
(a) N81°50'E
(b) N82°10'E
(c) N84°10'E
(d) N77°50'E
Ans: (c)
Magnetic Declination,δ = 2°E
Magnetic FB of AB = N 79°50' E
To find local attraction at station A
As station O is free from local attraction
Hence FB of OA will be correct,
Correct FB of OA = N 50°20' W ≌ 309°40'
∴ Correct BB of OA = 129°40'
∵ Obserbed FB of AO
= Observed BB of OA
= S52°40'E
= 127°20
Error = Observed bearing - Correct bearing
= 127°20' - 129°40'
= 2°20'
Correction = +2°20'
Local attraction at station A
= +2°20' ≌ 2°20' E
∴ Magnetic FB of AB = N 79°50'E
δ = 2°E and local attraction = 2°20'E
∴ TB of FB of AB = 79°50' + 2°20' + 2°
= N84°10'E
Q22: In a closed loop traverse of 1 km total length, the closing errors in departure and latitude are 0.3 m and 0.4 m, respectively. The relative precision of this traverse will be [2015 : 1 Mark, Set-I]
(a) 1 : 5000
(b) 1 : 4000
(c) 1 : 3000
(d) 1 : 2000
Ans: (d)
Relative precision 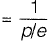
where, p = Perimeter of traverse
e = Closing error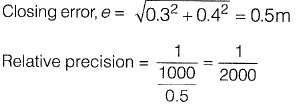
Q23: Group-I lists tool/instrument while Group-ll lists the method of surveying. Match the tool/ instrument with the corresponding method of surveying. [2014 : 2 Marks, Set-I]
Ans: (d)
1. Alllade: It is a straight edge ruler used in plane table surveying whichis used for sighting the objects and drawing the line son the drawing sheet.
2. Arrow: Arrows are used to mark the position of end of the hain or tape on the ground.
3. Bubble tube: It is used to check the level of the instrument. When the bubble of the tube comes in the centre, then the instrument in levelled.
4. Stadia hair: Lines on diaphragm, the intercept ‘S’ between 2 stadia hairs of a vertically held rod gives the distance between tacheometer and the road as
D = kS (k = stadia constant)
Q24: A Theodolite is placed at A and a 3 m long vertical staff is held at B. The depression angle made at reading of 2.5 m marking on staff is 6°10'. The horizontal distance between A and B is 2200 m. The height of instrument at A is 1.1 m and reduced level of point A is 880.88 m using curvature correction and refraction correction determine the R.L. of point B(in m)? [2013 : 2 Marks]
Ans: RL of A = 880.88 m
RL of plane of collimation
= 880.88 + 1.1 = 881.98 m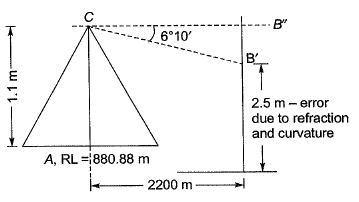

Here, D = Distance between theodolite and staff in km
∴ RL of B = 881.98-237.701
- (2.5 x 0.0673 x 2.22)
= 642.105 m
Q25: Bearing of the given system is shown below: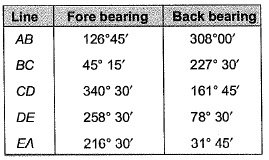 Applying correction due to local attraction, the correct bearing of line BC will be [2013 : 2 Marks]
Applying correction due to local attraction, the correct bearing of line BC will be [2013 : 2 Marks]
(a) 48°15'
(b) 50° 15'
(C) 49° 15'
(d) 48°45'
Ans: (d)
The difference between back bearing and fore bearing of line DE
= 258° 30' - 78° 30' = 180°
∴ Station D and E are free from local attraction
Fore bearing of line EA = 216° 30'
∴ Correct back bearing of line EA
= 216° 30' - 180° = 36° 30'
∴ Error at A = 31° 45' - 36° 30' = -4°45'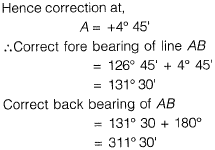
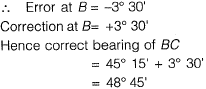
Q26: The latitude and departure of a line AB are +78 m and -45.1 m respectively. The whole circle bearing of the line AB is [2013 : 1 Mark]
(a) 30°
(b) 150°
(c) 210°
(d) 330°
Ans: (d)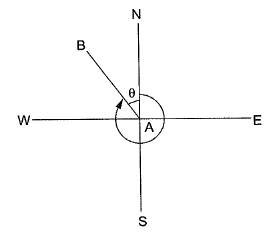 Since the latitude of line is positive and departure is negative, the line lies in the fourth quadrant.
Since the latitude of line is positive and departure is negative, the line lies in the fourth quadrant.
∴ L*cosθ = 78
L*sinθ = -45.1
⇒ tanθ = -0.578
θ = -30°
∴ WCB of AB = 360° - 30°
= 330°
Q27: The observations from a closed loop traverse around an obstacle are
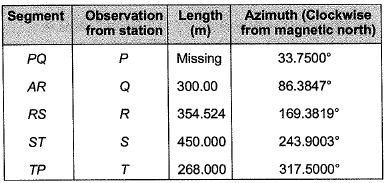 What is the value of the missing measurement (rounded off to the nearest 10 mm)? [2011 : 2 Marks]
What is the value of the missing measurement (rounded off to the nearest 10 mm)? [2011 : 2 Marks]
(a) 396.86 m
(b) 396.79 m
(c) 396.05 m
(d) 396.94 m
Ans: (b)
In a closed loop travers, the algebraic sum of all the latitudes should be equal to zeroi.e., ∑L = 0
⇒ Lcos 33.7500°+ 300 cos 86.3847° + 354.524 cos 169.3819° + 450 cos 243.900° + 268 cos 317.5° = 0
⇒ Lcos 33.75° = 329.9166
⇒ L = 396.79 m
FAQs on Past Year Questions: Compass & Traverse Surveying - Topic wise GATE Past Year Papers for Civil Engineering - Civil Engineering (CE)
| 1. What is the difference between compass surveying and traverse surveying? |  |
| 2. How do you perform a closed traverse survey? |  |
| 3. What are the common errors encountered in compass and traverse surveying? |  |
| 4. What are the advantages of using compass surveying? |  |
| 5. What instruments are typically used in traverse surveying? |  |
















