Past Year Questions: Precipitation & General Aspects of Hydrology | Topic wise GATE Past Year Papers for Civil Engineering - Civil Engineering (CE) PDF Download
Q1: A 2 m × 2 m tank of 3 m height has inflow, outflow and stirring mechanisms. Initially, the tank was half filled with fresh water. At t = 0, an inflow of salt a solution of concentration 5g/m3 at the rate of 2 litre/s and an outflow of the well stirred mixture at the rate of 1 litre/s are initiated. This process can be modeled using the following differential equation. wherem is the mass (grams) of salt at time t (seconds). The mass of the salt (in grams) in the tank at 75% of its capacity is ______(rounded off to 2 decimal places). [2024, Set-1]
Ans: 24.5 to 25.5
Sol: Total capacity of tank = 2 × 2 × 3 = 12 m3
At 50% capacity,
Volume (V50) = 0.5 × 12 = 6 m3
At 75% capacity,
Volume (V75) = 0.75 × 12 m3 = 9 m3
Now, increase in volume ΔV = V75 − V50 = (9−6)m3 = 3 m3
Also,
Inflow (I) = 2l/s
Outflow (Q) = 1l/s(Q) = 1l/s
Rate of change storage,
ΔS/Δt = I−Q = 2−1 = 1l/s
= 3000l / 1l/s = 3000sec
Now,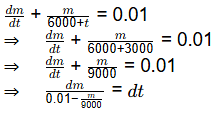 Integrating both sides
Integrating both sides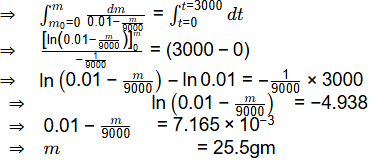
Q2: The return period of a large earthquake for a given region is 200 years. Assuming that earthquake occurrence follows Poisson's distribution, the probability that it will be exceeded at least once in 50 years is _______ %. (rounded off to the nearest integer). [2024, Set-1]
Ans: 21 to 23
Sol:
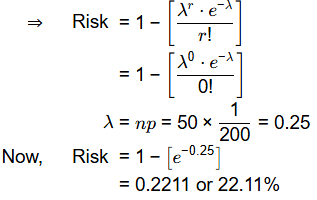
Q3: A catchment may be idealized as a circle of radius 30 km. There are five rain gauges, one at the center of the catchment and four on the boundary (equi-spaced), as shown in the figure (not to scale).
The annual rainfall recorded at these gauges in a particular year are given below.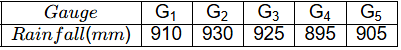 Using the Thiessen polygon method, what is the average rainfall (in mm, rounded off to two decimal places) over the catchment in that year? [2023, Set-2]
Using the Thiessen polygon method, what is the average rainfall (in mm, rounded off to two decimal places) over the catchment in that year? [2023, Set-2] Ans: 912.28 to 912.82
Ans: 912.28 to 912.82
Sol: Radius of basin = 30 km
We know that in Theissen polygon method, the polygons are obtained by joining the perpendicular bisectors of triangles formed, when various rain gauge stations are joined.
The Theissen polygon in the given basin can be drawn as:
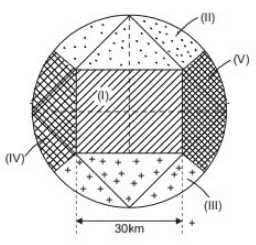
Area under influence of station Gl
= 30 × 30 = 900 km2
Area under influence of stations
G2, G3, G4, G5
= 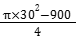
= 481.86 km2 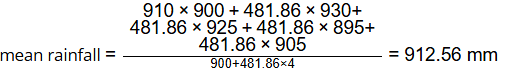
Q4: A tube-well of 20 cm diameter fully penetrates a horizontal, homogeneous and isotropic confined aquifer of infinite horizontal extent. The aquifer is of 30 m uniform thickness. A steady pumping at the rate of 40 litres/s from the well for a long time results in a steady drawdown of 4 m at the well face. The subsurface flow to the well due to pumping is steady, horizontal and Darcian and the radius of influence of the well is 245 m. The hydraulic conductivity of the aquifer (in m/day, round off to integer) is ______________ [2021 Set-1]
Ans: 34 to 38
Sol: 
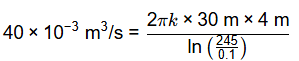
k = 4.14 × 10−4 m/s
or, k = 35.77 m/d
≈36 m/d( round off to nearest integer)
Q5: Two reservoirs are connected through a homogeneous and isotropic aquifer having hydraulic conductivity (K) of 25 m/day and effective porosity (η) of 0.3 as shown in the figure (not to scale). Ground water is flowing in the aquifer at the steady state.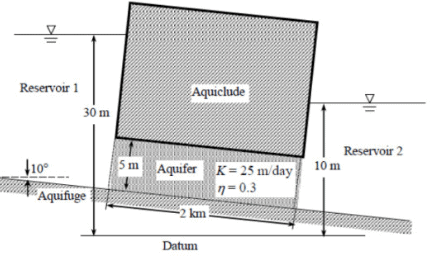 If water in Reservoir 1 is contaminated then the time (in days, round off to one decimal place) taken by the contaminated water to reach to Reservoir 2 will be _____________ [2021, Set-1]
If water in Reservoir 1 is contaminated then the time (in days, round off to one decimal place) taken by the contaminated water to reach to Reservoir 2 will be _____________ [2021, Set-1]
Ans: 2400
Sol:
k = 25 m/d
n = 0.3
i = 20 m / 2000 m = 0.01
V = ki
Vs = V/n
t = l / Vs
t = 2400 days
Q6: A catchment may be idealised as a rectangle. There are three rain gauges located inside the catchment at arbitrary locations. The average precipitation over the catchment is estimated by two methods: [2019, Set-1]
(i) Arithmetic mean (PA), and
(ii) Thiessen polygon (PT).
Which one of the following statements is correct?
(a) PA is always smaller than PT
(b) PA is always equal to PT
(c) There is no definite relationship between PA and PT
(d) PA is always greater than PT
Ans: (c)
Sol: The result from Thiessen polygon method is more accurate than arithmetic mean method. But there is no any close relationship between values obtained by Thiessen polygon method and Arithmetic mean method.
∴ There is no any relation between PA and PT.
Q7: Rainfall depth over a watershed is monitored through six number of well distributed rain gauges. Gauged data are given below:

The Thiessen mean value (in mm, up to one decimal place) of the rainfall is______ [2018, Set-1]
Ans: 478.5 to 479.5
Sol: Thiessen mean value of rainfall;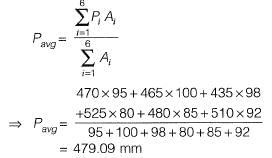
Q8: A catchment is idealized as a 25 km x 25 km square. It has five rain gauges, one at each corner and one at the center, as shown in the figure. During a month, the precipitation at these gauges is measured as G1 = 300 mm, G2 = 285 mm, G3 = 272 mm, G4 = 290 mm and G5 = 288 mm. The average precipitation (in mm, up to one decimal place) over the catchment during this month by using the Thiessen polygon method is [2017, Set-2]
During a month, the precipitation at these gauges is measured as G1 = 300 mm, G2 = 285 mm, G3 = 272 mm, G4 = 290 mm and G5 = 288 mm. The average precipitation (in mm, up to one decimal place) over the catchment during this month by using the Thiessen polygon method is [2017, Set-2]
Ans: 286.9 to 287.9
Sol: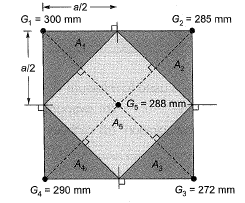 Let sides of square be, a = 25 km Now area of the polygon is calculated as,
Let sides of square be, a = 25 km Now area of the polygon is calculated as,
Q9: In a catchment, there are four rain-gauge stations, P, Q, Ft and S. Normal annual precipitation values at these stations are 780 mm, 850 mm, 920 mm and 980 mm, respectively. In the year 2013, stations Q, R and S, were operative but P was not. Using the normal ratio method, the precipitation at station P for the year 2013 has been estimated as 860 mm. If the observed precipitation at stations O and P for the year 2013 were 930 mm and 1010 mm, respectively; what was the observed precipitation (in mm) at station S for that year? [2015, Set-I]
Ans: 1093 to 1094
Sol: Let Pp = Precipitation in 2013 at station P
Np = Normal annual precipitation at station P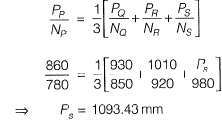
Q10: An isohyet is a line joining points of [2013]
(a) equal temperature
(b) equal humidity
(c) equal rainfall depth
(d) equal evaporation
Ans: (c)
FAQs on Past Year Questions: Precipitation & General Aspects of Hydrology - Topic wise GATE Past Year Papers for Civil Engineering - Civil Engineering (CE)
| 1. What is precipitation and how does it occur in the hydrological cycle? |  |
| 2. What factors influence the amount and distribution of precipitation in a region? |  |
| 3. How is precipitation measured and reported in meteorology? |  |
| 4. What are the different types of precipitation and how do they differ? |  |
| 5. Why is understanding precipitation important for water resource management? |  |

|
Explore Courses for Civil Engineering (CE) exam
|

|

















