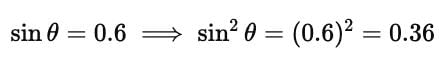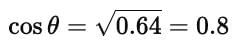Class 10 Exam > Class 10 Notes > Mathematics (Maths) Class 10 > Important Definitions & Formulas: Introduction to Trigonometry
Important Definitions & Formulas: Introduction to Trigonometry | Mathematics (Maths) Class 10 PDF Download
| Table of contents |

|
| Definitions and Formulas |

|
| Reciprocal Relations |

|
| Trigonometric Ratios of Some Specific Angles |

|
| Trigonometric Identities |

|
Definitions and Formulas
- An angle is positive if it is measured in the anticlockwise direction and negative if it is measured in the clockwise direction.
- In a right triangle ABC, right-angled at B
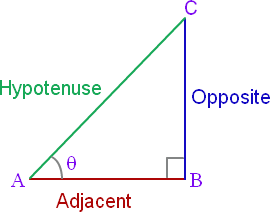

Reciprocal Relations
- If one of the trigonometric ratios of an acute angle is known, the remaining trigonometric ratios can be determined.
- Two angles are said to be complementary if their sum is 90°, and each one of them is called the complement of the other.
sin (90° - θ) = cos θ
cos (90° - θ) = sin θ
tan (90° - θ) = cot θ
cot (90° - θ) = tan θ
sec (90° - θ) = cosec θ
cosec (90° - θ) = sec θ
Question for Important Definitions & Formulas: Introduction to TrigonometryTry yourself:If the sine of an acute angle is known to be 0.6, what is the value of cos of the angle?
View Solution
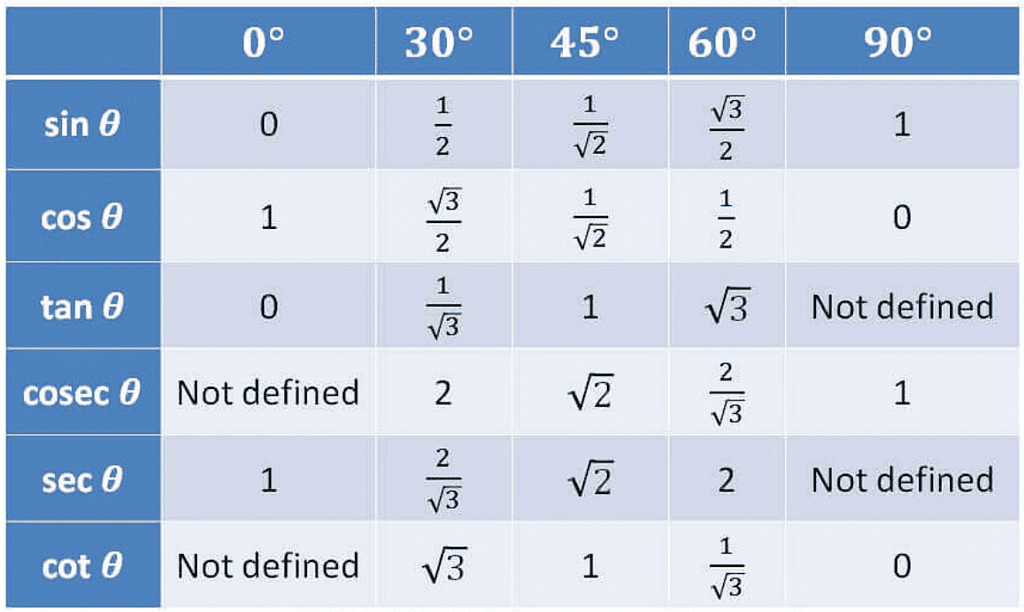
Trigonometric Ratios of Some Specific Angles
Trigonometric Identities
An equation with trigonometric ratios of an angle θ, which is true for all values of ‘θ’, for which the given trigonometric ratios are defined, is called an identity.
Three fundamental trigonometric identities are
(a) sin2θ + cos2θ = 1
(b) sec2θ = 1 + tan2θ
(c) cosec2θ = 1 + cot2θ
The document Important Definitions & Formulas: Introduction to Trigonometry | Mathematics (Maths) Class 10 is a part of the Class 10 Course Mathematics (Maths) Class 10.
All you need of Class 10 at this link: Class 10
|
127 videos|584 docs|79 tests
|
FAQs on Important Definitions & Formulas: Introduction to Trigonometry - Mathematics (Maths) Class 10
| 1. What is the definition of reciprocal relations in trigonometry? |  |
Ans. Reciprocal relations in trigonometry refer to the relationships between trigonometric functions like sine, cosine, tangent, cosecant, secant, and cotangent. These functions are reciprocals of each other, meaning that the value of one function is the reciprocal of the value of another function.
| 2. Can you provide an example of a trigonometric ratio of a specific angle? |  |
Ans. One example of a trigonometric ratio of a specific angle is the sine of 30 degrees, which is equal to 1/2. This means that in a right triangle with a 30-degree angle, the ratio of the length of the side opposite the angle to the length of the hypotenuse is 1/2.
| 3. What are some common trigonometric identities that are important to know? |  |
Ans. Some common trigonometric identities include the Pythagorean identities, sum and difference identities, double angle identities, and half-angle identities. These identities are useful in simplifying trigonometric expressions and solving trigonometric equations.
| 4. How can trigonometric identities be used in solving trigonometric equations? |  |
Ans. Trigonometric identities can be used to simplify complex trigonometric expressions, making it easier to solve equations involving trigonometric functions. By applying the appropriate identity, you can transform the equation into a simpler form that can be easily solved using algebraic techniques.
| 5. Why are trigonometric ratios of some specific angles important in trigonometry? |  |
Ans. Trigonometric ratios of some specific angles, such as 30, 45, and 60 degrees, are important because they are commonly used in mathematical calculations and real-world applications. Knowing these ratios allows for quick and accurate calculations in various trigonometric problems.
Related Searches