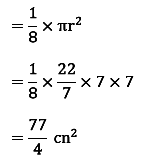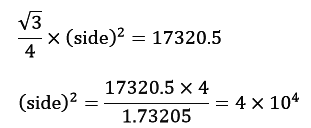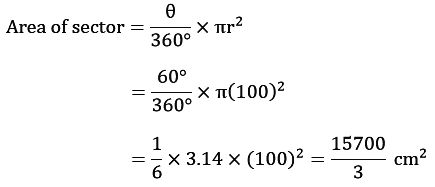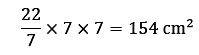Important Definitions & Formulas: Areas Related to Circles | Mathematics (Maths) Class 10 PDF Download
| Table of contents |

|
| Perimeter and Area of a Circle |

|
| Perimeter and Area of the Semi-circle |

|
| Area of a Ring |

|
| Areas of Sectors of a Circle |

|
| Length of an Arc of a Sector of Angle θ |

|
Perimeter and Area of a Circle
The perimeter of all the plain figures is the outer boundary of the figure. Likewise, the outer boundary of the circle is the perimeter of the circle. The perimeter of a circle is also called the Circumference of the Circle.
Radius = r and Diametre = d = 2rCircumference = 2πr = πd (π = 22/7)
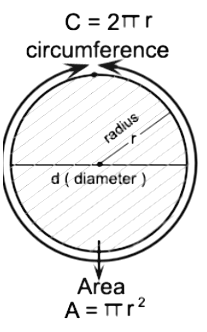 The area is the region enclosed by the circumference.
The area is the region enclosed by the circumference.
Area of the circle = πr2
Example: If a pizza is cut in such a way that it divides into 8 equal parts as shown in the figure, then what is the area of each piece of the pizza? The radius of the circle shaped pizza is 7 cm.
Solution: The pizza is divided into 8 equal parts, so the area of each piece is equal.
Area of 1 piece = 1/8 of area of circle
Perimeter and Area of the Semi-circle
The perimeter of the semi-circle is half of the circumference of the given circle plus the length of diameter as the perimeter is the outer boundary of the figure.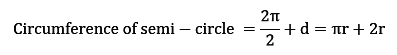
 Area of the semi-circle is just half of the area of the circle.
Area of the semi-circle is just half of the area of the circle.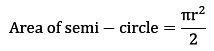
Area of a Ring
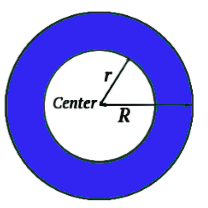
Area of the ring i.e. the coloured part in the above figure is calculated by subtracting the area of the inner circle from the area of the bigger circle.
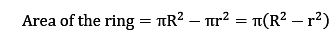
Where, R = radius of outer circle
r = radius of inner circle
Areas of Sectors of a Circle
The area formed by an arc and the two radii joining the endpoints of the arc is called Sector.
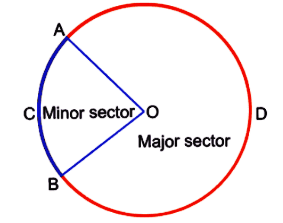
- Minor Sector: The area including ∠AOB with point C is called Minor Sector. So OACB is the minor sector. ∠AOB is the angle of the minor sector.

- Major Sector: The area including ∠AOB with point D is called the Major Sector. So OADB is the major sector. The angle of the major sector is 360° – ∠AOB.
Area of Major Sector = πr2 - Area of the Minor Sector
Remark: Area of Minor Sector + Area of Major Sector = Area of the Circle
Length of an Arc of a Sector of Angle θ
An arc is the piece of the circumference of the circle so an arc can be calculated as the θ part of the circumference.

Areas of Segments of the Circle
The area made by an arc and a chord is called the Segment of the Circle.
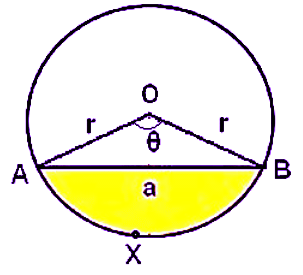
Minor Segment
The area made by chord AB and arc X is the minor segment. The area of the minor segment can be calculated by
Area of Minor Segment = Area of Minor Sector – Area of ∆ABO
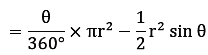
Major Segment
The other part of the circle except for the area of the minor segment is called a Major Segment.
Area of Major Segment = πr2 - Area of Minor Segment
Remark: Area of major segment + Area of minor segment = Area of circle
Areas of Combinations of Plane Figures
As we know how to calculate the area of different shapes, so we can find the area of the figures which are made with the combination of different figures.
Example: Find the area of the colored part if the given triangle is equilateral and its area is 17320.5 cm2. Three circles are made by taking the vertex of the triangles as the centre of the circle and the radius of the circle is the half of the length of the side of the triangle. (π = 3.14 and √3 = 1.73205)
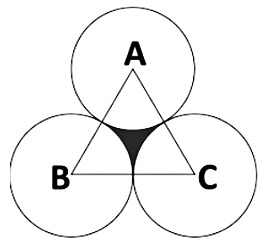
Solution: Given
ABC is an equilateral triangle, so ∠A, ∠B, ∠C = 60°
Hence the three sectors are equal, of angle 60°.
Required
To find the area of the shaded region.
Area of shaded region =Area of ∆ABC – Area of 3 sectors
Area of ∆ABC = 17320.5 cm2
Side = 200 cm
As the radius of the circle is half of the length of the triangle, so
Radius = 100 cm
Area of 3 Sectors = 3 × 15700/3 cm2 cm2
Area of shaded region = Area of ∆ABC – Area of 3 sectors
= 17320.5 - 15700 cm2
= 1620.5 cm2
Example: Find the area of the shaded part, if the side of the square is 8 cm and the 44 cm.
Solution: Required region = Area of circle – Area of square
= πr2 – (side)2
Circumference of circle = 2πr = 44
Radius of the circle = 7 cm
Area of circle = πr2
Area of square = (side) 2 = (8)2 = 64 cm2
Area of shaded region = Area of circle – Area of square
= 154 cm2 - 64 cm2
= 90 cm2
|
129 videos|736 docs|84 tests
|
FAQs on Important Definitions & Formulas: Areas Related to Circles - Mathematics (Maths) Class 10
| 1. What is the formula for calculating the perimeter of a circle? |  |
| 2. How do you find the area of a semi-circle? |  |
| 3. What is the formula for the area of a ring? |  |
| 4. How can I calculate the area of a sector of a circle? |  |
| 5. What is the formula for finding the length of an arc of a sector with angle θ? |  |