Class 10 Maths Previous Year Questions - Polynomials
| Table of contents |

|
| Previous Year Questions 2024 |

|
| Previous Year Questions 2023 |

|
| Previous Year Questions 2022 |

|
| Previous Year Questions 2021 |

|
| Previous Year Questions 2020 |

|
| Previous Year Questions 2019 |

|
Previous Year Questions 2024
Q1: What should be added from the polynomial x2 – 5x + 4, so that 3 is the zero of the resulting polynomial? (2024)(a) 1
(b) 2
(c) 4
(d) 5
 View Answer
View AnswerAns: (b)
Let, f(x) = x2 – 5x + 4
Let p should be added to f(x) then 3 becomes zero of polynomial.
So, f(3) + p = 0
⇒ 32 – 5 × 3 + 4 + p = 0
⇒ 9 + 4 – 15 + p = 0
⇒ – 2 + p = 0
⇒ p = 2
So, 2 should be added.
Q2: Find the zeroes of the quadratic polynomial x2 – 15 and verify the relationship between the zeroes and the coefficients of the polynomial. (2024)
 View Answer
View AnswerAns:
x2 – 15 = 0
x2 = 15
x = ± √15
Zeroes will be α = √15 , β = – √15
Verification: Given polynomial is x2 – 15
On comparing above polynomial with
ax2 + bx + c, we have
a = 1, b = 0, c = –15
sum of zeros = α + β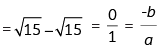
Product of zeros = αβ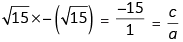
Hence, verified.
Previous Year Questions 2023
Q3: The graph of y = p(x) is given, for a polynomial p(x). The number of zeroes of p(x) from the graph is (2023)
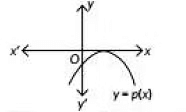 (a) 3
(a) 3
(b) 1
(c) 2
(d) 0
 View Answer
View AnswerAns: (b)
Here, y = p(x) touches the x-axis at one point
So, number of zeros is one.
Q4: If α, β are the zeroes of a polynomial p(x) = x2 + x - 1, then 1/α + 1/β equals to (2023)
(a) 1
(b) 2
(c) -1
(d) -1/2
 View Answer
View AnswerAns: (a)
The polynomial is p(x) = x2 + x - 1.
Step 1: The relationships between the zeroes and coefficients:
Sum of zeroes (α + β): - ba = - 11 = -1
Product of zeroes (αβ): ca = -11 = -1
Step 2: Simplify 1α + 1β:
1α + 1β = α + βαβ
Substitute the values:
α + βαβ = -1-1 = 1
Final Answer: (a) 1
Q5: If α, β are the zeroes of a polynomial p(x) = x2 - 1, then the value of (α + β) is (2023)
(a) 1
(b) 2
(c) -1
(d) 0
 View Answer
View AnswerAns: (d)
The polynomial is p(x) = x2 - 1.
Step 1: Sum of zeroes (α + β): - ba = - 01
Step 2: Simplify:
- 01 = 0
Final Answer: (d) 0
Q6: If α, β are the zeroes of a polynomial p(x) = 4x2 - 3x - 7, then (1/α + 1/β) is equal to (2023)
(a) 7/3
(b) -7/3
(c) 3/7
(d) -3/7
 View Answer
View AnswerAns: (d)
The polynomial is p(x) = 4x2 - 3x - 7.
Step 1: calculating sum and product of zeroes
Sum of zeroes (α + β): - ba = - (-3)4 = 34
Product of zeroes (αβ): ca = -74
Step 2: Simplify 1α + 1β:
α + βαβ = 34-74 = -37
Final Answer: (d) - 37
Q7: If one zero of the polynomial p(x) = 6x2 + 37x – (k – 2) is reciprocal of the other, then find the value of k. (CBSE 2023)
 View Answer
View AnswerAns: We have,
The polynomial is p(x) = 6x2 + 37x - (k - 2).
Step 1: The relationship between the product of zeroes and coefficients:
Product of zeroes (αβ): ca = -(k - 2)6
It is given that αβ = 1. Substitute this:
-(k - 2)6 = 1
Step 2: Solve for k:
Multiply both sides by 6:
-(k - 2) = 6
Simplify:
k - 2 = -6
k = -4
Final Answer: k = - 4
Previous Year Questions 2022
Q8: If one of the zeroes of a quadratic polynomial ( k - 1 )x2 + kx + 1 is - 3 , then the value of k is (2022)
(a) 4/3
(b) -4/3
(c) 2/3
(d) -2/3
 View Answer
View AnswerAns: (a)
Given. -3 is a zero of quadratic polynomial (k - 1)2+ kx + 1.
∴ (k - 1) (-3)2 + k(-3) +1 = 0
⇒ 9k - 9 - 3k + 1 = 0 ⇒ 6k - 8 = 0
⇒ k = 8/6
⇒ k = 4/3
Q9: If the path traced by the car has zeroes at -1 and 2, then it is given by (2022)
(a) x2 + x + 2
(b) x2 - x + 2
(c) x2 - x - 2
(d) x2 + x - 2
 View Answer
View AnswerAns: (c)
The zeroes of the polynomial are -1 and 2.
Step 1: The polynomial with given zeroes is:
p(x) = a(x - α)(x - β)
Substitute the zeroes α = -1 and β = 2:
p(x) = a(x - (-1))(x - 2) = p(x) = a(x + 1)(x - 2)
Step 2: Expand the polynomial:
p(x) = a[(x)(x) + (x)(-2) + (1)(x) + (1)(-2)]
p(x) = a[x2 - x - 2]
Step 3: Assuming a = 1:
p(x) = x2 - x - 2
Final Answer: (c) x2 - x - 2
Q10: The number of zeroes of the polynomial representing the whole curve, is (2022)
(a) 4
(b) 3
(c) 2
(d) 1
 View Answer
View AnswerAns: (a)
Given curve cuts the x-axis at four distinct points.
So, number of zeroes will be 4 .
Q11: The distance between C and G is (2022)
(a) 4 units
(b) 6 units
(c) 8 units
(d) 7 units
 View Answer
View AnswerAns: (b)
The distance between point C and G is 6 units.
Q12: The quadratic polynomial, the sum of whose zeroes is -5 and their product is 6. (2022)
(a) x2 + 5x + 6
(b) x2 - 5x + 6
(c) x2 - 5 x - 6
(d) - x2 + 5x + 6
 View Answer
View AnswerAns: (a)
Let α, β be the zeroes of required polynomial p(x).
Given, α + β=-5 and α.β=6
∴ p(x)=k[x2 - (-5)x + 6] = k[x2 + 5x + 6]
Thus, one of the polynomial which satisfy the given condition is x2+ 5x + 6
Previous Year Questions 2021
Q13: If one zero of the quadratic polynomial x2 + 3x + k is 2 then find the value of k. (2021) View Answer
View AnswerAns: Given, polynomial is f(x) =x2 + 3x + k
Since, 2 is zero of the polynomial f(x).
∴ f(2) = 0
⇒ f(2) =(2)2 + 3 x 2 + k
⇒ 4 + 6 + k = 0
⇒ k = -10
Previous Year Questions 2020
Q14: The degree of polynomial having zeroes -3 and 4 only is (2020)
(a) 2
(b) 1
(c) more than 3
(d) 3
 View Answer
View AnswerAns: (a)
Since, the polynomial has two zeroes only. So. the degree of the polynomial is 2.
Q15: If one of the zeroes of the quadratic polynomial x2 + 3x + k is 2. then the value of k is (2020)
(a) 10
(b) - 10
(c) -7
(d) -2
 View Answer
View AnswerAns: (b)
Given, 2 is a zero of the polynomial
p(x) = x2 + 3x + k
∴ p (2) = 0
⇒ (2)2 + 3(2) + k = 0
⇒ 4 + 6 + k = 0 =
⇒ 10 + k = 0
⇒ k= -10
Q16: The quadratic polynomial, the sum of whose zeroes is -5 and their product is 6________ is (2020)
(a) x2 + 5x + 6
(b) x2 - 5x + 6
(c) x2- 5x - 6
(d) -x2 + 5x + 6
 View Answer
View AnswerAns: (a)
Let α, β be the zeroes of required polynomial p(x)
Given, α+ β = -5 and αβ = 6
p(x) = k[x2 - (- 5)x + 6]
= k[x2 + 5x + 6]
Thus, one of the polynomial which satisfy the given condition is x2 + 5x + 6.
Q17: Form a quadratic polynomial, the sum and product of whose zeroes are (-3) and 2 respectively. (CBSE 2020)
 View Answer
View AnswerAns: Let α, β be the zeroes of required polynomial Given, α + β = -3 and αβ = 2
∴ p(x) = k[x2= - (-3)x + 2] = k(x2 + 3x + 2)
For k = 1 , p (x) = x2 + 3x + 2
Hence, one of the polynomial which satisfy the given condition is x2 + 3x + 2.
Q18: The zeroes of the polynomial x2 – 3x – m(m + 3) are:
(a) m, m + 3
(b) –m, m + 3
(c) m, – (m + 3)
(d) –m, – (m + 3) (CBSE 2020)
 View Answer
View AnswerAns: (b)
Given:
x2 − 3x − m(m + 3) = 0
Let's find the zeroes by applying the quadratic formula: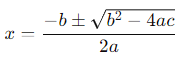
Substitute into the formula:
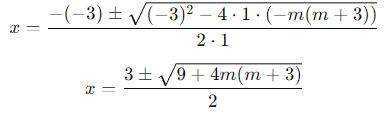
Simplify under the square root:
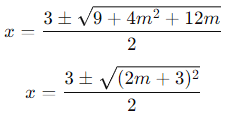
Taking the square root:
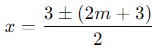
So, the zeroes are –m and m + 3.
Thus, the correct answer is (b) –m, m + 3.
Previous Year Questions 2019
Q19: Find the value of k such that the polynomial x2 - (k + 6)x + 2(2k - 1) has sum of its zeroes equal to half of their product. [Year 2019, 3 Marks] View Answer
View AnswerAns: 7
The given polynomial is x2 -(k + 6)x + 2(2k - 1)
According to the question
Sum of zeroes = 1/2(Product of Zeroes ):
⇒ k + 6 = 1/2 x 2 (2k - 1)
⇒ k + 6 = 2k - 1
⇒ k = 7
|
126 videos|457 docs|75 tests
|
FAQs on Class 10 Maths Previous Year Questions - Polynomials
| 1. What are polynomials in mathematics? |  |
| 2. How do you identify the degree of a polynomial? |  |
| 3. What is the difference between a monomial, binomial, and polynomial? |  |
| 4. How do you add and subtract polynomials? |  |
| 5. Why are polynomials important in Grade 10 mathematics? |  |



















