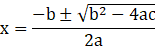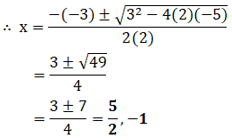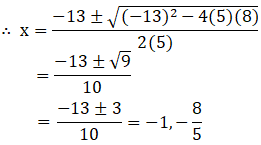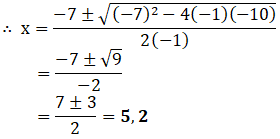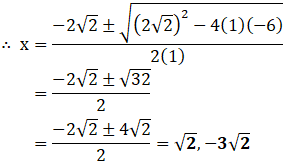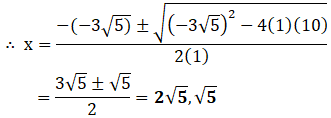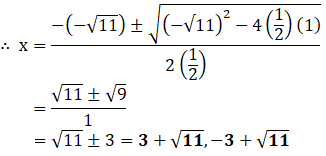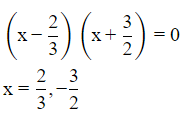NCERT Exemplar: Quadratic Equations - 1 | Mathematics (Maths) Class 10 PDF Download
Exercise 4.1
Choose the correct answer from the given four options in the following questions:
Q.1. Which of the following is a quadratic equation?
(a) x2 + 2x + 1 = (4 – x)2 + 3
(b) –2x2 = (5 – x)(2x-(2/5))
(c) (k + 1) x2 + (3/2) x = 7, where k = –1
(d) x3 – x2 = (x – 1)3
Correct Answer is Option (d)
The standard form of a quadratic equation is given by,
ax2 + bx + c = 0, a ≠ 0
(A) Given, x2 + 2x + 1 = (4 – x)2 + 3
x2 + 2x + 1 = 16 – 8x + x2 + 3
10x – 18 = 0
which is not a quadratic equation.
(B) Given, -2x2 = (5 – x) (2x – 2/5)
-2x2 = 10x – 2x2 – 2 +2/5x
52x – 10 = 0
which is not a quadratic equation.
(C) Given, (k + 1) x2 + 3/2 x = 7, where k = -1
(-1 + 1) x2 + 3/2 x = 7
3x – 14 = 0
which is not a quadratic equation.
(D) Given, x3 – x2 = (x – 1)3
x3 – x2 = x3 – 3x2 + 3x – 1
2x2 – 3x + 1 = 0
which represents a quadratic equation.
Q.2. Which of the following is not a quadratic equation?
(a) 2(x – 1)2 = 4x2 – 2x + 1
(b) 2x – x2 = x2 + 5
(c) (√2x + √3)2 + x2 = 3x2 − 5x
(d) (x2 + 2x)2 = x4 + 3 + 4x3
Correct Answer is Option (c)
A quadratic equation is represented by the form,
ax2 + bx + c = 0, a ≠ 0
(a) Given, 2(x – 1)2 = 4x2 – 2x + 1
2(x2 – 2x + 1) = 4x2 – 2x + 1
2x2 + 2x – 1 = 0
which is a quadratic equation.
(b) Given, 2x – x2 = x2 + 5
2x2 – 2x + 5 = 0
which is a quadratic equation.
(c) Given, (√2x + √3)2 + x2= 3x2 – 5x
2x2 + 2√6x + 3 + x2= 3x2 – 5x
(5 + 2√6)x + 3 = 0
which is not quadratic equation, it is a linear equation.
(d) Given, (x2 + 2x)2 = x4 + 3 + 4x3
x4 + 4x3 + 4x2 = x4 + 3 + 4x3
4x2 – 3 = 0
which is a quadratic equation.
Q.3. Which of the following equations has 2 as a root?
(a) x2 – 4x + 5 = 0
(b) x2 + 3x – 12 = 0
(c) 2x2 – 7x + 6 = 0
(d) 3x2 – 6x – 2 = 0
Correct Answer is Option (c)
If 2 is a root then substituting the value 2 in place of x should satisfy the equation.
(a) Given,
x2 – 4x + 5 = 0
(2)2 – 4(2) + 5 = 1 ≠ 0
So, x = 2 is not a root of x2 – 4x + 5 = 0
(b) Given, x2 + 3x – 12 = 0
(2)2 + 3(2) – 12 = -2 ≠ 0
So, x = 2 is not a root of x2 + 3x – 12 = 0
(c) Given, 2x2 – 7x + 6 = 0
2(2)2 – 7(2) + 6 = 0
Here, x = 2 is a root of 2x2 – 7x + 6 = 0
(d) Given, 3x2 – 6x – 2 = 0
3(2)2 – 6(2) – 2 = -2 ≠ 0
So, x = 2 is not a root of 3x2 – 6x – 2 = 0
Q.4. If ½ is a root of the equation x2 + kx – 5/4 = 0, then the value of k is
(a) 2
(b) – 2
(c) ¼
(d) ½
Correct Answer is Option (a)
If ½ is a root of the equation
x2 + kx – 5/4 = 0 then, substituting the value of ½ in place of x should give us the value of k.
Given, x2 + kx – 5/4 = 0 where, x = ½
(½)2 + k (½) – (5/4) = 0
(k/2) = (5/4) – ¼
k = 1
Q.5. Which of the following equations has the sum of its roots as 3?
(a) 2x2 – 3x + 6 = 0
(b) –x2 + 3x – 3 = 0
(c) √2x2 – 3/√2x + 1 = 0
(d) 3x2 – 3x + 3 = 0
Correct Answer is Option (b)
The sum of the roots of a quadratic equation ax2 + bx + c = 0, a ≠ 0 is given by,
Coefficient of x / coefficient of x2 = – (b/a)
(a) Given, 2x2 – 3x + 6 = 0
Sum of the roots = – b/a = -(-3/2) = 3/2
(b) Given, -x2 + 3x – 3 = 0
Sum of the roots = – b/a = -(3/-1) = 3
(c) Given, √2x2 – 3/√2x+1=0
2x2 – 3x + √2 = 0
Sum of the roots = – b/a = -(-3/2) = 3/2
(d) Given, 3x2 – 3x + 3 = 0
Sum of the roots = – b/a = -(-3/3) = 1
Q.6. Values of k for which the quadratic equation 2x2 – kx + k = 0 has equal roots is
(a) 0 only
(b) 4
(c) 8 only
(d) 0, 8
Correct Answer is Option (d)
Given, the equation is 2x² - kx + k = 0
We have to find the values of k for which the equation has equal roots.
A quadratic equation ax² + bx + c = 0 has equal roots when the discriminant of the equation is zero.
Discriminant = b² - 4ac
Here, a = 2, b = -k and c = k
(-k)² - 4(2)(k) = 0
k² - 8k = 0
k(k - 8) = 0
k = 0
k - 8 = 0
k = 8
Therefore, the roots of the equation are 0 and 8.
Q.7. Which constant must be added and subtracted to solve the quadratic equation 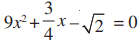 by the method of completing the square?
by the method of completing the square?
(a) 1/8
(b) 1/64
(c) 1/4
(d) 9/64
Correct Answer is Option (b)
Given, the quadratic equation is 9x² + (3/4)x - √2 = 0
We have to find the constant to be added and subtracted to solve the quadratic equation by the method of completing the square.
Let y = 3x
Now, (3x)² + (3x)/4 - √2 = 0
y² + (1/4)y - √2 = 0 --------------------- (1)
By using algebraic identity,
(a + b)² = a² + 2ab + b² --------------------- (2)
Comparing (1) and (2),
a² = 1
a = 1
2ab = 1/4
2(1)b = 1/4
b = 1/8
b² = (1/8)² = 1/64
So, y² + (1/4)y - √2 + 1/64 - 1/64 = 0
On rearranging,
y² + (1/4)y + 1/64 - √2 - 1/64 = 0
(y + 1/8)² = √2 + 1/64
Now, (3x + 1/8)² = √2 + 1/64
Therefore, the constant to be added and subtracted is 1/64.
Q.8. The quadratic equation 2x2 – √5x + 1 = 0 has
(a) two distinct real roots
(b) two equal real roots
(c) no real roots
(d) more than 2 real roots
Correct Answer is Option (c)
Given, the quadratic equation is 2x² - √5x + 1 = 0
We have to find the nature of the roots of the equation.
Discriminant = b² - 4ac
Here, a = 2, b = -√5 and c = 1
b² = (-√5)² = 5
4ac = 4(2)(1) = 8
b² - 4ac = 5 - 8 = -3
b² - 4ac < 0
A quadratic equation ax² + bx + c = 0 has no real roots when the discriminant of the equation is less than zero.
Therefore, the equation has no real roots.
Q.9. Which of the following equations has two distinct real roots?
(a) 2x2 -3√2x + 9/4 = 0
(b) x2 + x – 5 = 0
(c) x2 + 3x + 2√2 = 0
(d) 5x2 – 3x + 1 = 0
Correct Answer is Option (b)
We have to find the equation which has two distinct real roots.
A quadratic equation ax² + bx + c = 0 has 2 distinct real roots when the discriminant of the equation is greater than zero.
Discriminant = b² - 4ac
From the options,
(a) 2x² - 3√2x + 9/4 = 0
Here, a = 2, b = -3√2 and c = 9/4
b² - 4ac = (-3√2)² - 4(2)(9/4)
= 18 - 18
= 0
Therefore, the equation has equal roots.
(b) x² + x - 5 = 0
Here, a = 1, b = 1 and c = -5
b² - 4ac = (1)² - 4(1)(-5)
= 1 + 20
= 21 > 0
Therefore, the equation has 2 distinct real roots.
(c) x² + 3x + 2√2 = 0
Here, a = 1, b = 3 and c = 2√2
b² - 4ac = (3)² - 4(1)(2√2)
= 9 - 8√2 < 0
Therefore, the equation has no real roots.(d) 5x² - 3x + 1 = 0
Here, a = 5, b = -3 and c = 1
b² - 4ac = (-3)² - 4(5)(1)
= 9 - 20
= -11 < 0
Therefore, the equation has no real roots.
Q.10. Which of the following equations has no real roots?
(a) x2 – 4x + 3√2 = 0
(b) x2 + 4x – 3√2 = 0
(c) x2 – 4x – 3√2 = 0
(d) 3x2 + 4√3x + 4 = 0
Correct Answer is Option (a)
We have to find an equation that has no real roots.
A quadratic equation ax² + bx + c = 0 has no real roots when the discriminant of the equation is less than zero.
Discriminant = b² - 4ac
From the options,
(a) x² - 4x + 3√2 = 0
Here, a = 1, b = -4 and c = 3√2
b² - 4ac = (-4)² - 4(1)(3√2)
= 16 - 12√2
= 16 - 12(1.414)
= 16 - 16.968
= -0.968 < 0
Therefore, the equation has no real roots.
(b) x² + 4x - 3√2 = 0
Here, a = 1, b = 4 and c = -3√2
b² - 4ac = (4)² - 4(1)(-3√2)
= 16 + 12√2 > 0
Therefore, the equation has 2 distinct real roots.
(c) x² - 4x - 3√2 = 0
Here, a = 1, b = -4 and c = -3√2
b² - 4ac = (-4)² - 4(1)(-3√2)
= 16 + 12√2 > 0
Therefore, the equation has 2 distinct real roots.
(d) 3x² + 4√3x + 4 = 0
Here, a = 3, b = 4√3 and c = 4
b² - 4ac = (4√3)² - 4(3)(4)
= 48 - 48
= 0
Q.11. (x2 + 1)2 – x2 = 0 has
(a) four real roots
(b) two real roots
(c) no real roots
(d) one real root.
Correct Answer is Option (c)
Given, the equation is (x² + 1)² - x² = 0
We have to find the nature of the roots of the equation.
By using algebraic identity,
(a + b)² = a² + 2ab + b²
(x² + 1)² = x⁴ + 2x² + 1
So, x⁴ + 2x² + 1 - x² = 0
By grouping,
x⁴ + 2x² - x² + 1 = 0
x⁴ + x² + 1 = 0
Let y = x²
So, y² + y + 1 = 0
Here, a = 1, b = 1 and c = 1
Discriminant = b² - 4ac = (1)² - 4(1)(1)
= 1 - 4= -3 < 0
A quadratic equation ax² + bx + c = 0 has no real roots when the discriminant of the equation is less than zero.
Therefore, the equation has no real roots.
Hence, the correct answer is option [c].
Exercise 4.2
Q.1. State whether the following quadratic equations have two distinct real roots. Justify your answer.
(i) x2 – 3x + 4 = 0
(ii) 2x2 + x – 1 = 0
(iii) 2x2 – 6x + 9/2 = 0
(iv) 3x2 – 4x + 1 = 0
(v) (x + 4)2 – 8x = 0
(vi) (x – √2)2 – 2(x + 1) = 0
(vii) √2 x2 –(3/√2)x + 1/√2 = 0
(viii) x (1 – x) – 2 = 0
(ix) (x – 1) (x + 2) + 2 = 0
(x) (x + 1) (x – 2) + x = 0
(i) The equation x2 – 3x + 4 = 0 has no real roots.
D = b2 – 4ac
= (-3)2 – 4(1)(4)
= 9 – 16 < 0
Hence, the roots are imaginary.
(ii) The equation 2x2 + x – 1 = 0 has two real and distinct roots.
D = b2 – 4ac
= 12 – 4(2) (-1)
= 1 + 8 > 0
Hence, the roots are real and distinct.
(iii) The equation 2x2 – 6x + (9/2) = 0 has real and equal roots.
D = b2 – 4ac
= (-6)2 – 4(2) (9/2)
= 36 – 36 = 0
Hence, the roots are real and equal.
(iv) The equation 3x2 – 4x + 1 = 0 has two real and distinct roots.
D = b2 – 4ac
= (-4)2 – 4(3)(1)
= 16 – 12 > 0
Hence, the roots are real and distinct.
(v) The equation (x + 4)2 – 8x = 0 has no real roots.
Simplifying the above equation,
x2 + 8x + 16 – 8x = 0
x2 + 16 = 0
D = b2 – 4ac
= (0) – 4(1) (16) < 0
Hence, the roots are imaginary.
(vi) The equation (x – √2)2 – √2(x+1)=0 has two distinct and real roots.
Simplifying the above equation,
x2 – 2√2x + 2 – √2x – √2 = 0
x2 – √2(2+1)x + (2 – √2) = 0
x2 – 3√2x + (2 – √2) = 0
D = b2 – 4ac
= (– 3√2)2 – 4(1)(2 – √2)
= 18 – 8 + 4√2 > 0
Hence, the roots are real and distinct.
(vii) The equation √2x2 – 3x/√2 + ½ = 0 has two real and distinct roots.
D = b2 – 4ac
= (- 3/√2)2 – 4(√2) (½)
= (9/2) – 2√2 > 0
Hence, the roots are real and distinct.
(viii) The equation x (1 – x) – 2 = 0 has no real roots.
Simplifying the above equation,
x2 – x + 2 = 0
D = b2 – 4ac
= (-1)2 – 4(1)(2)
= 1 – 8 < 0
Hence, the roots are imaginary.
(ix) The equation (x – 1) (x + 2) + 2 = 0 has two real and distinct roots.
Simplifying the above equation,
x2 – x + 2x – 2 + 2 = 0
x2 + x = 0
D = b2 – 4ac
= 12 – 4(1)(0)
= 1 – 0 > 0
Hence, the roots are real and distinct.
(x) The equation (x + 1) (x – 2) + x = 0 has two real and distinct roots.
Simplifying the above equation,
x2 + x – 2x – 2 + x = 0
x2 – 2 = 0
D = b2 – 4ac
= (0)2 – 4(1) (-2)
= 0 + 8 > 0
Hence, the roots are real and distinct.
Q.2. Write whether the following statements are true or false. Justify your answers.
(i) Every quadratic equation has exactly one root.
(ii) Every quadratic equation has at least one real root.
(iii) Every quadratic equation has at least two roots.
(iv) Every quadratic equations has at most two roots.
(v) If the coefficient of x2 and the constant term of a quadratic equation have opposite signs, then the quadratic equation has real roots.
(vi) If the coefficient of x2 and the constant term of a quadratic equation have the same sign , then the quadratic equation has no real roots.
(i) False. For example, a quadratic equation x2 – 9 = 0 has two distinct roots – 3 and 3.
(ii) False. For example, equation x2 + 4 = 0 has no real root.
(iii) False. For example, a quadratic equation x2 – 4x + 4 = 0 has only one root which is 2.
(iv) True, because every quadratic polynomial has almost two roots.
(v) True, because in this case discriminant is always positive.
For example, in ax2+ bx + c = 0, as a and c have opposite sign, ac < 0
⟹ Discriminant = b2 – 4ac > 0.
(vi) True, because in this case discriminant is always negative.
For example, in ax2+ bx + c = 0, as b = 0, and a and c have same sign then ac > 0
⟹ Discriminant = b2 – 4ac = – 4 a c < 0
Q.3. A quadratic equation with integral coefficient has integral roots. Justify your answer.
No, a quadratic equation with integral coefficients may or may not have integral roots.
Justification
Consider the following equation,
8x2 – 2x – 1 = 0
The roots of the given equation are ½ and – ¼ which are not integers.
Hence, a quadratic equation with integral coefficient might or might not have integral roots.
Q.4. Does there exist a quadratic equation whose coefficients are rational but both of its roots are irrational? Justify your answer.
Yes, for this Discriminant should not be a perfect square.
Consider the quadratic equation 2x2 +x−4=0, which has rational coefficients.
The roots of the given quadratic equation arewhich are irrational.
Q.5. Does there exist a quadratic equation whose coefficients are all distinct irrationals but both the roots are rationals? Why?
Yes, consider the quadratic equation with all distinct irrationals coefficients i.e. √ 3x2−7√3x +12√3 = 0. The roots of this quadratic equation are 3 and 4, which are rationals.
Q.6. Is 0.2 a root of the equation x2 – 0.4 = 0? Justify.
Given, the quadratic equation is x² - 0.4 = 0
We have to determine if 0.2 is a root of the equation.
Put x = 0.2 in the equation,
x² - 0.4 = (0.2)² - 0.4
= 0.04 - 0.4
= -0.36
Therefore, 0.2 is not a root of the equation.
Q.7. If b = 0, c < 0, is it true that the roots of x2 + bx + c = 0 are numerically equal and opposite in sign? Justify.
Given, the equation is x² + bx + c = 0.
b = 0 and c < 0
We have to determine if the roots of the equation are numerically equal and opposite in sign.
Using the quadratic formula,
x = [-b ± √b² - 4ac]/2a
Here, a = 1, b = 0
Since c < 0 take c as -c.
x = [-0 ± √0 - 4(1)(-c)]/2(1)
x = ± √4c/2
x = ± c
Therefore, the roots are c and -c.
Exercise 4.3
Q.1. Find the roots of the quadratic equations by using the quadratic formula in each of the following:
(i) 2 x2 – 3x – 5 = 0
(ii) 5x2 + 13x + 8 = 0
(iii) –3x2 + 5x + 12 = 0
(iv) –x2 + 7x – 10 = 0
(v) x2 + 2 √2x – 6 = 0
(vi) x2 – 3 √5x + 10 = 0
(vii) (½)x2– √11x + 1 = 0
The quadratic formula for finding the roots of quadratic equation
ax2 + bx + c = 0, a ≠ 0 is given by,
(i) 2 x2 – 3x – 5 = 0
(ii) 5x2 + 13x + 8 = 0
(iv) –x2 + 7x – 10 = 0
(v) x2 + 2 √2x – 6 = 0
(vi) x2 – 3 √5x + 10 = 0
(vii) (½)x2– √11x + 1 = 0
Q.2. Find the roots of the following quadratic equations by the factorisation method:
(i) 2x2 + 5/3x - 2 = 0
(ii) 2/5x2 - x - 3/5 = 0
(iii) 3√2 x2 – 5x – √2 = 0
(iv) 3x2 + 5√5x - 10 = 0
(v) 21x2 -2x + 1/21 = 0
(i) Given,
2x2 + 5/3x - 2 = 0
⇒6x2 +5x−6=0
6x2 −4x+9x−6=0
2x(3x−2)+3(3x−2)=0
(3x−2)(2x+3)=0
(ii) Given, the quadratic equation is (2/5)x² - x - 3/5 = 0.
We have to find the roots of the equation by factorisation method.
The equation can be written as
2x² - 5x - 3 = 0
On factoring,
2x² - 6x + x - 3 = 0
2x(x - 3) + 1(x - 3) = 0
(2x + 1)(x - 3) = 0
Now, 2x + 1 = 0
2x = -1
x = -1/2
Also, x - 3 = 0
x = 3
Therefore, the roots of the equation are 3 and -1/2.(iii) Given, the quadratic equation is 3√2x² - 5x - √2 = 0.
We have to find the roots of the equation by factorisation method.
On factoring,
3√2x² - 5x - √2 = 0
3√2x² - 6x + x - √2 = 0
3√2x(x - √2) + 1(x - √2) = 0
(3√2x + 1)(x - √2) = 0
Now, 3√2x + 1 = 0
3√2x = -1
x = -1/3√2
Also, x - √2 = 0
x = √2
Therefore, the roots of the equation are √2 and -1/3√2.(iv) Given, the quadratic equation is 3x² + 5√5x - 10 = 0.
We have to find the roots of the equation by factorisation method.
On factoring,
3x² + 6√5x - √ 5x - 10 = 0
3x(x + 2√5) - √5(x + 2√5) = 0
(3x - √5)(x + 2√5) = 0
Now, 3x - √5 = 0
3x = √5
x = √5/3
Also, x + 2√5 = 0
x = -2√5
Therefore, the roots of the equation are -2√5 and √5/3.(v) Given, the quadratic equation is 21x² - 2x + 1/21 = 0.
We have to find the roots of the equation by factorisation method.
The equation can be written as
441x² - 42x + 1 = 0
On factoring,
441x² - 21x - 21x + 1 = 0
21x(21x - 1) - (21x - 1) = 0
(21x - 1)(21x - 1) = 0
Now, 21x - 1 = 0
21x = 1
x = 1/21
Therefore, the roots of the equation are 1/21 and 1/21.
|
127 videos|584 docs|79 tests
|
FAQs on NCERT Exemplar: Quadratic Equations - 1 - Mathematics (Maths) Class 10
| 1. How to solve quadratic equations by factorization? |  |
| 2. What is the quadratic formula and how is it used to solve quadratic equations? |  |
| 3. How many solutions can a quadratic equation have? |  |
| 4. Can a quadratic equation have no solutions? |  |
| 5. How can the graph of a quadratic equation help in solving it? |  |