NCERT Exemplar: Arithmetic Progressions | Mathematics (Maths) Class 10 PDF Download
Exercise 5.1
Choose the correct answer from the given four options in the following questions:Q1: In an AP, if d = –4, n = 7, an = 4, then a is
(a) 6
(b) 7
(c) 20
(d) 28
Correct Answer is option (d)
We know that nth term of an AP is
an = a + (n – 1)d
where,
a = first term
an is nth term
d is the common difference
According to the question,
4 = a + (7 – 1)(- 4)
4 = a – 24
a = 24 + 4 = 28
Q2: In an AP, if a = 3.5, d = 0, n = 101, then an will be
(a) 0
(b) 3.5
(c) 103.5
(d) 104.5
Correct Answer is option (b)
We know that nth term of an AP is
an = a + (n – 1)d
Where,
a = first term
an is nth term
d is the common difference
an = 3.5 + (101 – 1)0
= 3.5
(Since, d = 0, it’s a constant A.P)
Q3: The list of numbers – 10, – 6, – 2, 2,… is
(a) an AP with d = – 16
(b) an AP with d = 4
(c) an AP with d = – 4
(d) not an AP
Correct Answer is option (b)
According to the question,
a1 = – 10
a2 = – 6
a3 = – 2
a4 = 2
a2 – a1 = 4
a3 – a2 = 4
a4 – a3 = 4
a2 – a1 = a3 – a2 = a4 – a3 = 4
Therefore, it’s an A.P with d = 4
Q4: The 11th term of the AP: –5, (–5/2), 0, 5/2, …is
(a) –20
(b) 20
(c) –30
(d) 30
Correct Answer is option (b)
First term, a = – 5
Common difference,
d = 5 – (-5/2) = 5/2
n = 11
We know that the nth term of an AP is
an = a + (n – 1)d
Where,
a = first term
an is nth term
d is the common difference
a11 = – 5 + (11 – 1)(5/2)
a11 = – 5 + 25 = 20
Q5: The first four terms of an AP, whose first term is –2 and the common difference is –2, are
(a) – 2, 0, 2, 4
(b) – 2, 4, – 8, 16
(c) – 2, – 4, – 6, – 8
(d) – 2, – 4, – 8, –16
Correct Answer is option (c)
First term, a = – 2
Second Term, d = – 2
a1 = a = – 2
We know that the nth term of an AP is
an = a + (n – 1)d
Where,
a = first term
an is nth term
d is the common difference
Hence, we have,
a2 = a + d = – 2 + (- 2) = – 4
Similarly,
a3 = – 6
a4 = – 8
So the A.P is
– 2, – 4, – 6, – 8
Q6: The 21st term of the AP whose first two terms are –3 and 4 is
(a) 17
(b) 137
(c) 143
(d) –143
Correct Answer is option (b)
First two terms of an AP are a = – 3 and a2 = 4.
We know, nth term of an AP is
an = a + (n – 1)d
Where,
a = first term
an is nth term
d is the common difference
a2 = a + d
4 = – 3 + d
d = 7
Common difference, d = 7
a21 = a + 20d
= – 3 + (20)(7)
= 137
Q7: If the 2nd term of an AP is 13 and the 5th term is 25, what is its 7th term?
(a) 30
(b) 33
(c) 37
(d) 38
Correct Answer is option (b)
We know that the nth term of an AP is
an = a + (n – 1)d
Where,
a = first term
an is nth term
d is the common difference
a2 = a + d = 13 …..(1)
a5 = a + 4d = 25 …… (2)
From equation (1) we have,
a = 13 – d
Using this in equation (2), we have
13 – d + 4d = 25
13 + 3d = 25
3d = 12
d = 4
a = 13 – 4 = 9
a7 = a + 6d
= 9 + 6(4)
= 9 + 24 = 33
Q8: Which term of the AP: 21, 42, 63, 84… is 210?
(a) 9th
(b) 10th
(c) 11th
(d) 12th
Correct Answer is option (b)
Let nth term of the given AP be 210.
According to question,
first term, a = 21
common difference, d = 42 – 21 = 21 and an = 210
We know that the nth term of an AP is
an = a + (n – 1)d
Where,
a = first term
an is nth term
d is the common difference
210 = 21 + (n – 1)21
189 = (n – 1)21
n – 1 = 9
n = 10
So, 10th term of an AP is 210.
Q9: If the common difference of an AP is 5, then what is a18 – a13?
(a) 5
(b) 20
(c) 25
(d) 30
Correct Answer is option (c)
Given, the common difference of AP i.e., d = 5
Now,
As we know, nth term of an AP is
an = a + (n – 1)d
where a = first term
an is nth term
d is the common difference
a18 -a13 = a + 17d – (a + 12d)
= 5d
= 5(5)
= 25
Q10: What is the common difference of an AP in which a18 – a14 = 32?
(a) 8
(b) – 8
(c) – 4
(d) 4
Correct Answer is option (a)
An arithmetic progression (AP) is a sequence where the two consecutive terms have the same common difference. It is obtained by adding the same fixed number to its previous term.
The nth term of an AP is
aₙ = a + (n - 1 )d.
a = first term
aₙ = nth term
d = common difference.
Given,
a₁₈ - a₁₄ = 32
a + (18 - 1)d - [a + (14 - 1)d] = 32.
a + 17d - a - 13d = 32.
17d - 13d = 32.
4d = 32
d = 8.
Therefore, d = 8.
Q11: Two APs have the same common difference. The first term of one of these is –1 and that of the other is – 8. Then the difference between their 4th terms is
(a) –1
(b) – 8
(c) 7
(d) –9
Correct Answer is option (c)
An arithmetic progression (AP) is a sequence where the two consecutive terms have the same common difference. It is obtained by adding the same fixed number to its previous term.
The nth term of an AP is
aₙ = a + (n - 1 )d.
a = first term
aₙ = nth term
d = common difference.
Let the common difference be d₁ and d₂.
By the condition given,
d₁ = d₂ = d -------------- (i)
The first term of the first AP be (a₁) = -1
The first term of the second AP be (a₂) = -8.
4th term of first AP,
T₄ = a₁ + (4 - 1)d
T₄ = -1 + 3d.
4th term of second AP,
T₄‘ = a₂ + (4 - 1)d
T₄‘ = -8 + 3d.
The difference between their 4th terms is
꘡T₄ - T₄’꘡= (-1 + 3d) - (-8 + 3d)
꘡T₄ - T₄’꘡= -1 + 3d + 8 - 3d = 7
꘡T₄ - T₄’꘡= 7.
Therefore, the required difference is 7.
Q12: If 7 times the 7th term of an AP is equal to 11 times its 11th term, then its 18th term will be
(a) 7
(b) 11
(c) 18
(d) 0
Correct Answer is option (d)
An arithmetic progression (AP) is a sequence where the two consecutive terms have the same common difference. It is obtained by adding the same fixed number to its previous term.
The nth term of an AP is
aₙ = a + (n - 1 )d.
a = first term
aₙ = nth term
d = common difference.
As per the question,
7a₇ = 11a₁₁
Since,aₙ = a + (n - 1 )d.
7[a + (7 - 1)d] = 11 [a + (11 - 1)d]
7(a + 6d) = 11 (a + 10d)
7a + 42d = 11a + 110d
42d -110d = 11a - 7a
4a + 68 d = 0
2(2a + 34d) = 0
2a + 34d = 0
a + 17d = 0----------------------(1)
18th term of an AP is
a₁₈ = a + (18 - 1)d
a₁₈ = a + 17d
a₁₈ = 0.
Therefore, the a₁₈ =0.
Q13: The 4th term from the end of the AP: -11, -8, -5, ..., 49 is
(a) 37
(b) 40
(c) 43
(d) 58
Correct Answer is option (b)
An arithmetic progression (AP) is a sequence where the two consecutive terms have the same common difference. It is obtained by adding the same fixed number to its previous term.
The nth term of an AP from the end is
aₙ = l -(n - 1)d ------(1)
a = first term
aₙ = nth term
d = common difference.
l = Last term.
From the question,
l = 49
d = -8 - (-11) = -8 + 11 = 3
From(1),we get,
a₄ = 49 - (4 - 1) 3
a₄ = 49 - 3(3)
a₄ = 49 - 9
a₄ = 40.
Therefore, the 4th term is 40.
Q14: The famous mathematician associated with finding the sum of the first 100 natural numbers is
(a) Pythagoras
(b) Newton
(c) Gauss
(d) Euclid
Correct Answer is option (c)
An arithmetic progression (AP) is a sequence where the two consecutive terms have the same common difference. It is obtained by adding the same fixed number to its previous term.
Gauss is the famous mathematician associated with finding the sum of 100 natural numbers.
Therefore, the famous mathematician is Gauss.
Q15: If the first term of an AP is –5 and the common difference is 2, then the sum of the first 6 terms is
(a) 0
(b) 5
(c) 6
(d) 15
Correct Answer is option (a)
An arithmetic progression (AP) is a sequence where the two consecutive terms have the same common difference. It is obtained by adding the same fixed number to its previous term.
From the question:
a = -5
d = 2.
The formula to find the sum is
Sn = n/2 [2a + (n - 1)d].
Substituting the values, we get,
S₆ = 6/2 [2a + (6 - 1)d]
S₆ = 3[2(-5) + 5(2)]
S₆ = 3(-10 + 10)
S₆ = 3(0)
S₆ = 0.
Therefore, S₆ = 0.
Q16: The sum of the first 16 terms of the AP: 10, 6, 2,... is
(a) –320
(b) 320
(c) –352
(d) –400
Correct Answer is option (a)
An arithmetic progression (AP) is a sequence where the two consecutive terms have the same common difference. It is obtained by adding the same fixed number to its previous term.
From the question given,
AP is 10, 6, 2,
a = 10
d = - 4.
The formula to find the sum is
Sn = n/2 [2a + (n - 1)d].
S₁₆ = 16/2 [2a + (16 - 1)d]
S₁₆ = 8[2 × 10 + 15(-4)]
S₁₆ = 8(20 - 60)
S₁₆ = 8(-40)
S₁₆ = -320.
Therefore, S₁₆ = -320.
Q17: In an AP if a = 1, an = 20 and Sn = 399, then n is
(a) 19
(b) 21
(c) 38
(d) 42
Correct Answer is option (c)
An arithmetic progression (AP) is a sequence where the two consecutive terms have the same common difference. It is obtained by adding the same fixed number to its previous term.
From the question,
a = 1
aₙ = 20
Sₙ = 399.
The formula to find the sum is
Sₙ = n/2 [2a + (n - 1)]d.
Substituting the values, we get,
399 = n/2 [2 × 1 + (n - 1)d].
798 = 2n + n(n - 1)d -----------(1)
Since, aₙ = a + (n - 1)d
a + (n-1)d = 20
1 + (n - 1)d = 20
(n - 1)d = 19 -----------(2)
Substituting (2) in(1), we get,
798 = 2n + 19 n
798 = 21n
n = 798/21.
Therefore, n = 798/21 = 38
Q18: The sum of the first five multiples of 3 is
(a) 45
(b) 55
(c) 65
(d) 75
Correct Answer is option (a)
An arithmetic progression (AP) is a sequence where the two consecutive terms have the same common difference. It is obtained by adding the same fixed number to its previous term.
From the question,
The first five multiples of 3 are 3, 6, 9,12 and 15.
First term, a = 3,
common difference, d = 6 - 3 = 3 and
number of terms, n = 5
The formula to find the sum is
Sₙ = n/2 [2a + (n - 1)d.
Substituting the values
S₅ = 5/2 [2a + (5 - 1)d]
S₅ = 5/2 [2 × 3 + 4 × 3]
So we get
S₅ = 5/2 (6 + 12)
S₅ = 5 × 9
S₅ = 45.
Therefore, S₅ = 45.
Exercise 5.2
Q1: Which of the following forms an AP? Justify your answer.
(i) –1, –1, –1, –1,…
We have a1 = – 1 , a2 = – 1, a3 = – 1 and a4 = – 1
a2 – a1 = 0
a3 – a2 = 0
a4 – a3 = 0
Clearly, the difference of successive terms is same, therefore given list of numbers from an AP.
(ii) 0, 2, 0, 2,…
We have a1 = 0, a2 = 2, a3 = 0 and a4 = 2
a2 – a1 = 2
a3 – a2 = – 2
a4 – a3 = 2
Clearly, the difference of successive terms is not same, therefore given list of numbers does not form an AP.
(iii) 1, 1, 2, 2, 3, 3…
We have a1 = 1 , a2 = 1, a3 = 2 and a4 = 2
a2 – a1 = 0
a3 – a2 = 1
Clearly, the difference of successive terms is not same, therefore given list of numbers does not form an AP.
(iv) 11, 22, 33…
We have a1 = 11, a2 = 22 and a3 = 33
a2 – a1 = 11
a3 – a2 = 11
Clearly, the difference of successive terms is same, therefore given list of numbers form an AP.
(v) 1/2,1/3,1/4, …
We have a1 = ½ , a2 = 1/3 and a3 = ¼
a2 – a1 = -1/6
a3 – a2 = -1/12
Clearly, the difference of successive terms is not same, therefore given list of numbers does not form an AP.
(vi) 2, 22, 23, 24, …
We have a1 = 2 , a2 = 22, a3 = 23 and a4 = 24
a2 – a1 = 22 – 2 = 4 – 2 = 2
a3 – a2 = 23 – 22 = 8 – 4 = 4
Clearly, the difference of successive terms is not same, therefore given list of numbers does not form an AP.
(vii) √3, √12, √27, √48, …
We have,
a1 = √3, a2 = √12, a3 = √27 and a4 = √48
a2 – a1 = √12 – √3 = 2√3 – √3 = √3
a3 – a2 = √27 – √12 = 3√3 – 2√3 = √3
a4 – a3 = √48 – √27 = 4√3 – 3√3 = √3
Clearly, the difference of successive terms is same, therefore given list of numbers from an AP.
Q2: Justify whether it is true to say that –1, -3/2, –2, 5/2,… forms an AP as
a2 – a1 = a3 – a2.
False
a1 = -1, a2 = -3/2, a3 = -2 and a4 = 5/2
a2 – a1 = -3/2 – (-1) = – ½
a3 – a2 = – 2 – (- 3/2) = – ½
a4 – a3 = 5/2 – (-2) = 9/2
Clearly, the difference of successive terms in not same, all though, a2 – a1 = a3 – a2 but a4 – a3 ≠ a3 – a2 therefore it does not form an AP.
Q3: For the AP: –3, –7, –11, …, can we find directly a30 – a20 without actually finding a30 and a20? Give reasons for your answer.
True
Given,
First term, a = – 3
Common difference, d = a2 – a1 = – 7 – (- 3) = – 4
a30 – a20 = a + 29d – (a + 19d)
= 10d
= – 40
It is so because difference between any two terms of an AP is proportional to common difference of that AP
Q4: Two APs have the same common difference. The first term of one AP is 2 and that of the other is 7. The difference between their 10th terms is the same as the difference between their 21st terms, which is the same as the difference between any two corresponding terms. Why?
Suppose there are two AP’s with first terms a and A
And their common differences are d and D respectively
Suppose n be any term
an = a + (n – 1)d
An = A + (n – 1)D
As common difference is equal for both AP’s
We have D = d
Using this we have
An – an = a + (n – 1)d – [ A + (n – 1)D]
= a + (n – 1)d – A – (n – 1)d
= a – A
As a – A is a constant value
Therefore, difference between any corresponding terms will be equal to a – A.
Q5: Is 0 a term of the AP: 31, 28, 25, ...? Justify your answer.
An arithmetic progression (AP) is a sequence where the two consecutive terms have the same common difference. It is obtained by adding the same fixed number to its previous term.
Let 0 be the nth term of given AP, (aₙ = 0)
From the question given,
a = 31,
d = 28 - 31 = - 3
The nth terms of an AP, is
aₙ = a + (n - 1 )d.
Substituting the values, we get,
0 = 31 + (n - 1)(-3)
3(n - 1) = 31.
Dividing both sides by 3, we get,
n - 1 = 31/3.
n = 31/3+ 1
n = 34/3.
As, n should be a positive integer, 0 is not a term given in the AP.
Therefore, 0 is not a term of the given AP.
Q6: The taxi fare after each km, when the fare is Rs 15 for the first km and Rs. 8 for each additional km, does not form an AP as the total fare (in Rs.) after each km is 15, 8, 8, 8, ... Is the statement true? Give reasons.
From the question above,
False,because the total fare after each km is 15.
From the question above,
t₁ = 15,
t₂ = 23,
t₃ = 31,
t₄ = 39.
Calculating the difference, we get,
t₂ - t₁ = 23 - 15 = 8
t₃ - t₂ = 31 - 23 = 8
t₄ - t₃ = 39 - 31 = 8
Since, each of the successive terms of the given list have the same difference (d=8).
Therefore, the total fare after each km forms an AP.
Q7: In which of the following situations, do the lists of numbers involved form an AP?
Give reasons for your answers.
(i) The fee charged from a student every month by a school for the whole session, when the monthly fee is Rs. 400.
(ii) The fee charged every month by a school from Classes I to XII, when the monthly fee for Class I is Rs. 250, and it increases by Rs. 50 for the next higher class.
(iii) The amount of money in the account of Varun at the end of every year when Rs. 1000 is deposited at simple interest of 10% per annum.
(iv) The number of bacteria in a certain food item after each second, when they double in every second.
Sol: (i) The fee charged from a student every month by a school for the whole session, when the monthly fee is Rs. 400.
From the question given,
The fee charged from a student every month by a school for the whole session is 400,400,400,400,....
Calculating the difference, we get,
Common difference, d = 0.
Since the difference between each successive term of the given list of numbers is 0.
Therefore, it forms an AP, with a common difference, d = 0.
(ii) The fee charged every month by a school from Classes I to XII, when the monthly fee for Class I is Rs. 250, and it increases by Rs. 50 for the next higher class.
From the question given,
The monthly fee from I to XII is 250, (250+50), (250 + 2 × 50), (250 + 3 × 50),….
(250, 300, 350, 400,….)
Calculating the difference, we get,
d1 = 300 - 250 = 50
d2 = 350 - 300 = 50
d3 = 400 - 350 = 50
Since, the d = 50 is the same for all, i.e. d1 = d2 = d3. The above statement forms an AP.
Therefore a given list of numbers formed by monthly fees from I to XII forms an AP.
Therefore, it forms an A.P with a common difference 50.
(iii) The amount of money in the account of Varun at the end of every year when Rs. 1000 is deposited at simple interest of 10% per annum.
Simple Interest = Principal × rate × time/100.
From the question given,
Simple Interest = 1000× 10 × 1/100 = 100.
Hence, the amount of money in the account at end of every year is
1000, (1000 + 100 × 1), (1000 + 100 × 2), (1000 + 100 × 3),….. = 1000, 1100, 1200, 1300,….
Calculating the difference, we get,
d1 = 1100 - 1000 = 100
d2 = 1200 - 1100 = 100
d3 = 1300 - 1200 = 100
Since, the d = 100 is the same for all, d1 = d2 = d3, the given list of numbers forms an AP.
Therefore, it forms an A.P with a common difference 100
(iv) The number of bacteria in a certain food item after each second, when they double in every second.
Let the number of bacteria present in food initially be x.
Since, they double in every second , x, 2x, 2(2x), 2(2 . 2 . x),…= x, 2x, 4x, 8x,…
From the question given,
t₁ = x,
t₂ = 2x,
t₃ = 4x
t₄ = 8x.
Calculating the difference,we get,
t₂ - t₁ = 2x - x = x
t₃ - t₂ = 4x - 2x = 2x
t₄ - t₃ = 8x - 4x = 4x.
Hence, the difference between each successive term is not the same.
Therefore, the list does not form an AP.
Q8: Justify whether it is true to say that the following are the nth terms of an AP.
(i) 2n–3
(ii) 3n2 + 5
(iii) 1 + n + n2
Sol: (i) 2n–3
Yes.
Ac cording to the question,
aₙ = 2n - 3
Substituting the value of n, we get
n = 1, a₁ = 2(1) - 3 = -1
n = 2, a₂ = 2(2) - 3 = 1
n = 3, a₃ = 2(3) - 3 = 3
n = 4, a₄ = 2(4) - 3 = 5
Hence, the sequence becomes -1, 1, 3, 5….
Calculating the difference, we get,
a₂ - a₁ = 1 - (-1) = 1 + 1 = 2
a₃ - a₂ = 3 - 1 = 2
a₄ - a₃ = 5 - 3 = 2.
So, we get,
a₂ - a₁ = a₃ - a₂ = a₄ - a₃
Therefore, 2n - 3 is the nth term of an AP.
(ii) 3n2 + 5
No.
According to the question,
aₙ = 3n² + 5
Substituting the value of n, we get,
n = 1, a₁ = 3(1)2 + 5 = 8
n = 2, a₂ = 3(2)2 + 5 = 3(4) + 5 = 17
n = 3, a₁ = 3(3)2 + 5 = 3(9) + 5 = 27 + 5 = 32
Hence, the sequence becomes 8, 17, 32,….
Calculating the difference, we get,
a₂ - a₁ = 17 - 8 = 9
a₃ - a₂ = 32 -17 = 15.
So, we get,
a₂ - a₁ ≠ a₃ - a₂
Since, the difference of each successive term is not the same, it does not form an AP.
Therefore, it does not form an AP.
(iii) 1 + n + n2
No.
According to the question,
aₙ = 1 + n + n²
Substituting the values of n, we get,
n = 1, a₁ = 1 + 1 + (1)² = 3
n = 2, a₂ = 1 + 2 + (2)² = 1 + 2 + 4 = 7
n = 3, a₃ = 1 + 3 + (3)² = 1+ 3 + 9 = 13
Hence, the sequence becomes 3, 7, 13,…
Calculating the difference, we get,
a₂ - a₁ = 7 - 3 = 4
a₃ - a₂ = 13 - 7 = 6.
So, we get,
a₂ - a₁ ≠ a₃ - a₂
Since, the difference of each successive term is not the same, it does not form an AP.
Therefore, it does not form an AP.
Exercise 5.3
Q1: Match the APs given in column A with suitable common differences given in column B.
(A1) AP is 2, – 2, – 6, – 10, ….
So common difference is simply
a2 – a1 = – 2 – 2 = – 4 = (B3)
(A2) Given
First term, a = – 18
No of terms, n = 10
Last term, an = 0
By using the nth term formula
an = a + (n – 1)d
0 = – 18 + (10 – 1)d
18 = 9d
d = 2 = (B5)
(A3) Given
First term, a = 0
Tenth term, a10 = 6
By using the nth term formula
an = a + (n – 1)d
a10 = a + 9d
6 = 0 + 9d
d = 2/3 = (B6)
(A4) Let the first term be a and common difference be d
Given that
a2 = 13
a4 = 3
a2 – a4 = 10
a + d – (a + 3d) = 10
d – 3d = 10
– 2d = 10
d = – 5= (B1)
Q2: Verify that each of the following is an AP, and then write its next three terms.
(i) 0, 1/4, 1/2, 3/4,…
Here,
a1 = 0
a2 = ¼
a3 = ½
a4 = ¾
a2 – a1 = ¼ – 0 = ¼
a3 – a2 = ½ – ¼ = ¼
a4 – a3 = ¾ – ½ = ¼
Since, difference of successive terms are equal,
Hence, 0, 1/4, 1/2, 3/4… is an AP with common difference ¼.
Therefore, the next three term will be,
¾ + ¼ , ¾ + 2(¼), ¾ + 3(¼)
1, 5/4 , 3/2
(ii) 5, 14/3, 13/3, 4…
Here,
a1 = 5
a2 = 14/3
a3 = 13/3
a4 = 4
a2 – a1 = 14/3 – 5 = -1/3
a3 – a2 = 13/3 – 14/3 = -1/3
a4 – a3 = 4 – 13/3 = -1/3
Since, difference of successive terms are equal,
Hence, 5, 14/3, 13/3, 4… is an AP with common difference -1/3.
Therefore, the next three term will be,
4 + (-1/3), 4 + 2(-1/3), 4 + 3(-1/3)
11/3 , 10/3, 3
(iii) √3 , 2√3, 3√3,…
Here,
a1 = √3
a2 = 2√3
a3 = 3√3
a4 = 4√3
a2 – a1 = 2√3 – √3 = √3
a3 – a2 = 3√3 – 2√3= √3
a4 – a3 = 4√3 – 3√3= √3
Since, difference of successive terms are equal,
Hence, √3 , 2√3, 3√3,… is an AP with common difference √3.
Therefore, the next three term will be,
4√3 + √3, 4√3 + 2√3, 4√3 + 3√3
5√3, 6√3, 7√3
(iv) a + b, (a + 1) + b, (a + 1) + (b + 1), …
Here
a1 = a + b
a2 = (a + 1) + b
a3 = (a + 1) + (b + 1)
a2 – a1 = (a + 1) + b – (a + b) = 1
a3 – a2 = (a + 1) + (b + 1) – (a + 1) – b = 1
Since, difference of successive terms are equal,
Hence, a + b, (a + 1) + b, (a + 1) + (b + 1), … is an AP with common difference 1.
Therefore, the next three term will be,
(a + 1) + (b + 1) + 1, (a + 1) + (b + 1) + 1(2), (a + 1) + (b + 1) + 1(3)
(a + 2) + (b + 1), (a + 2) + (b + 2), (a + 3) + (b + 2)
(v) a, 2a + 1, 3a + 2, 4a + 3,…
Here a1 = a
a2 = 2a + 1
a3 = 3a + 2
a4 = 4a + 3
a2 – a1 = (2a + 1) – (a) = a + 1
a3 – a2 = (3a + 2) – (2a + 1) = a + 1
a4 – a3 = (4a + 3) – (3a+2) = a + 1
Since, difference of successive terms are equal,
Hence, a, 2a + 1, 3a + 2, 4a + 3,… is an AP with common difference a + 1.
Therefore, the next three term will be,
4a + 3 +(a + 1), 4a + 3 + 2(a + 1), 4a + 3 + 3(a + 1)
5a + 4, 6a + 5, 7a + 6
Q3: Write the first three terms of the APs when a and d are as given below:
(i) a = 1/2, d = -1/6
(ii) a = –5, d = –3
(iii) a = 2 , d = 1/√2
Sol: (i) a =1/2, d = -1/6
We know that,
First three terms of AP are:
a, a + d, a + 2d
½, ½ + (-1/6), ½ + 2 (-1/6)
½, 1/3, 1/6
(ii) a = –5, d = –3
We know that,
First three terms of AP are:
a, a + d, a + 2d
-5, – 5 + 1 (- 3), – 5 + 2 (- 3)
– 5, – 8, – 11
(iii) a = √2 , d = 1/√2
We know that,
First three terms of AP are:
a, a + d, a + 2d
√2, √2+1/√2, √2+2/√2
√2, 3/√2, 4/√2
Q4: Find a, b and c such that the following numbers are in AP: a, 7, b, 23, c
For a, 7, b, 23, c… to be in AP
it has to satisfy the condition,
a5 – a4 = a4 – a3 = a3 – a2 = a2 – a1 = d
Where d is the common difference
7 – a = b – 7 = 23 – b = c – 23 …(1)
Let us equate,
b – 7 = 23 – b
2b = 30
b = 15 (eqn 1)
And,
7 – a = b – 7
From eqn 1
7 – a = 15 – 7
a = – 1
And,
c – 23 = 23 – b
c – 23 = 23 – 15
c – 23 = 8
c = 31
So a = – 1
b = 15
c = 31
Then, we can say that, the sequence – 1, 7, 15, 23, 31 is an AP
Q5: Determine the AP whose fifth term is 19 and the difference of the eighth term from the thirteenth term is 20.
We know that,
The first term of an AP = a
And, the common difference = d.
According to the question,
5th term, a5 = 19
Using the nth term formula,
an = a + (n – 1)d
We get,
a + 4d = 19
a = 19 – 4d …(1)
Also,
13th term – 8th term = 20
a + 12d – (a + 7d) = 20
5d = 20
d = 4
Substituting d = 4 in equation 1,
We get,
a = 19 – 4(4)
a = 3
Then, the AP becomes,
3, 3 + 4 , 3 + 2(4),…
3, 7, 11,…
Q6: The 26th, 11th and the last term of an AP are 0, 3 and -⅕ respectively. Find the common difference and the number of terms.
Consider the first term, common difference and number of terms of an AP are a, d and n, respectively.
If last term of an AP is known,
l = 8 + (11-1 )d …………. (i)
So nth term of an AP is
Tn = a + (n - 1)d …………. (ii)
We know that,
26th term of an AP = 0
T26 = a + (26 - 1 )d = 0 [from Equation (i)]
8 + 25d = 0 …………. (iii)
11th term of an AP = 3
T11 = s + (11 - 1)d = 3 [from Equation (ii)]
8 + 10d = 3 ……………… (iv)
Last term of an AP = -⅕
l = a + (n - 1 )d [from Equation (i)]
-1/5 = a + (n - 1 )d ………… (v)
Now, subtracting Equation (iv) from Equation (iii),
15 d = - 3
d = -⅕
Substitute the value of d in Equation (iii),
a + 25(-⅕) = 0
a - 5 = 0
a = 5
Substitute the value of a, d in Equation (v), we get
-1/5 = 5 + (n - 1)(-1/5)
-1 = 25 - (n - 1)
-1 = 25 - n + 1
n = 25 + 2 = 27
Therefore, the common difference and number of terms are -1/ 5 and 27.
Q7: The sum of the 5th and the 7th terms of an AP is 52 and the 10th term is 46. Find the AP.
Consider the first term and common differences of AP are a and d.
From the question,
a5 + a7 = 52
a10 = 46
a + (5 - l)d + a + (7 - 1)d = 52
We know that
an = a + (n- 1 )d]
a + (10 - 1 )d = 4
⇒ a + 4d + a + 6d = 52
Similarly a + 9d = 46
⇒ 2a + 10d = 52
and a + 9d = 46
⇒ a + 5d = 26 ………….. (i)
a + 9d = 46 ……………. (ii)
By subtracting Equation (i) from Equation (ii),
4d = 20
d = 5
From Equation (i)
a = 26 - 5(5) = 1
The required AP is a, a + d, a + 2d, a + 3d ….
i.e., 1, 1 + 5, 1 + 2(5), 1 + 3(5)…
i.e., 1, 6,11,16,….
Therefore, the AP is 1, 6, 11, 16, …..
Q8: Find the 20th term of the AP whose 7th term is 24 less than the 11th term, the first term being 12.
Consider the first term, common difference and number of terms of an AP are a, d and n.
We know that
First term (a) = 12
From the given condition,
7th term (T7) = 11th term (T11) - 24
The nth term of an AP, Tn = a + (n - 1 )d
⇒ a + (7 - 1)d = a + (11 - l)d - 24
⇒ a + 6d = a + 10d - 24
⇒ 24 = 4d
Dividing both sides by 4
⇒ d = 6
So the 20th term of AP,
T20 = a + (20 - 1)d
Substituting the values
= 12 + 19 × 6
= 126
Therefore, the 20th term of an AP is 126.
Q9: If the 9th term of an AP is zero, prove that its 29th term is twice its 19th term.
An arithmetic progression (AP) is a sequence where the differences between every two consecutive terms are the same.
Consider the first term, common difference and number of terms of an AP are a, d and n.
We know that,
9th term of an AP, T9 = 0
So the nth term of an AP, Tn = a + (n - 1 )d
⇒ a + (9 - 1)d = 0
⇒ a + 8d = 0 ⇒ a = -8 d ………….. (i)
The 19th term, T19 = a + (19 - 1)d
= -8d + 18d [From Equation (i)
= 10d …………… (ii)
The 29th term, T29 = a + (29 - 1)d
= -8d + 28d
= 20d
= 2 × (10d) [from Equation (i)]
⇒ T29 = 2 × T19
Therefore, it is proved.
Q10: Find whether 55 is a term of the AP: 7, 10, 13,--- or not. If yes, find which term it is.
Consider the first term, common difference and the number of terms of an AP are a, d and n.
nth term of an AP is Tn = 55
We know that the nth term of an AP,
Tn = a + (n - 1 )d …………….. (i)
It is given,
first term (a) = 7
common difference (d) = 10 - 7 = 3
From equation (i),
55 = 7 + (n - 1) × 3
55 = 7 + 3n - 3
55 = 4 + 3n
3n = 51
Dividing both sides by 3
n = 17
n is a positive integer. So 55 is a term of the AP as n = 17
Therefore, the 17th term of an AP is 55.
Q11: Determine k so that k2+ 4k + 8, 2k2 + 3 k + 6, 3k2 + 4 k + 4 are three consecutive terms of an AP.
It is given that
k² + 4k + 8, 2k² + 3k + 6 and 3k² + 4k+ 4 are consecutive terms of an AP.
2k²+ 3k + 6- (k² + 4k + 8)
= 3k² + 4k + 4 - (2k² + 3k + 6) is the Common difference
By multiplying the negative sign
2k² + 3k + 6 - k² - 4k - 8 = 3k² + 4k + 4 - 2k² - 3k - 6
k² - k - 2 = k² + k - 2
-k = k
2k = 0
k = 0
Therefore, k is 0.
Q12: Split 207 into three parts such that these are in AP and the product of the two smaller parts is 4623.
Consider the three parts of the number 207 are (a - d), a and (a + d), which are in AP.
From the given condition,
Sum of these parts = 207
a - d + a + a + d = 207
3a = 207
Dividing both sides by 3
a = 69
It is given that,
Product of the two smaller parts = 4623
a(a -d) = 4623
Substituting the values
69 . (69 - d) = 4623
69 - d = 67
So we get
d = 69 - 67 = 2
First part = a - d = 69 - 2 = 67,
Second part = a = 69
Third part = n + d = 69 + 2 = 71
Therefore, the required three parts are 67, 69, 71.
Q13: The angles of a triangle are in AP. The greatest angle is twice the least. Find all the angles of the triangle.
Given ,
The angles of a triangle are in AP.
Consider A, B and C are angles of a ∆ABC
B = (A + C)/2
2B = A + C …(i)
We know that, the sum of all interior angles of a ∆ABC is 180°
A + B + C = 180°
2B + B = 180° [from Equation (i)]
3B = 180°
B = 60°
Let A and C be the greatest and least angles
A = 2C …………. (ii)
Substituting the values of B and A in Equation (i),
2 × 60° = 2C + C
120° = 3 C
C = 40°
Substitute value of C in Equation (ii),
A = 2 × 40°
A = 80°
Therefore, all the angles of a triangle are 80°, 60° and 40°.
Q14: If the nth terms of the two APs: 9, 7, 5, ... and 24, 21, 18,... are the same, find the value of n. Also, find that term.
Consider the first term, common difference and number of terms of the AP: 9, 7, 5,…. are
a1, d1 and n1
First term (a1) = 9
Common difference (d1) = 7 - 9 = -2
T’n1 = a1 + (n1 - 1) d
= 9+ (n1 - 1) (-2)
= 9 - 2n1 + 2
T’n1 = 11 - 2n1 ….. (i)
The nth term of an AP is
Tn = a + (n - 1) d
Consider the first term, common difference, and the number of terms of the AP: 24, 21, 18, … are a2, d2, and n2
First term, (a2) = 24
Common difference (d2) = 21 - 24 = -3
The nth term T’’n2 = a2 + (n2 - 1)d2
T”n2 = 24 + (n2 - 1) (-3)
T”n2 = 24 - 3n2 + 3
T”n2 = 27 - 3n2 …. (ii)
From the given condition the nth term of both AP is same
11 - 2n1 = 27 - 3n2
So we get
n = 16
The nth term of first AP is
T’n1 = 11 - 2n1 = 11 - 2 (16) = 11 - 32 = -21
The nth term of second AP is
T”n2 = 27 - 3n2 = 27 - 3 (16) = 27 - 48 = -21
Therefore, the value of n is 16 and that term i.e., nth term is -21.
Q15: If sum of the 3rd and the 8th terms of an AP is 7 and the sum of the 7th and the 14th terms is –3, find the 10th term.
Consider the first term and common difference of an AP are a and d.
From the question,
a3 + a8 = 7 and a17 + a14 = -3
a + (3 - 1)d + a + (8 - 1)d = 7
We know that an = a + (n- 1 )d
a + (7 - 1 )d + a + (14 - 1 )d = -3
a + 2d + a + 7d = 7
a + 6d + a + 13d = -3
2a + 9d = 7 ………….. (i)
2a + 19d = -3 …(ii)
By subtracting equation (i) from equation (ii),
10d = -10
d = -1
2a + 9(-1) = 7 [from equation (i)]
2a - 9 = 7
2a = 16
Dividing both sides by 2
a = 8
So we get
a10 = a + (10 - 1)d
= 8 + 9(-1)
= 8 - 9
= -1
Therefore, the 10th term is -1.
Q16: Find the 12th term from the end of the AP: –2, –4, –6,..., –100.
It is given that
AP : -2, -4, -6,…., -100
First term (a) = -2,
Common difference (d) = -4 - (-2) = -2
Last term (l) = -100
The nth term of an AP from the end
an = l - (n - 1 )d,
where l is the last term
d is the common difference.
So the 12th term from the end,
a12 = -100 - (12 - 1)(-2)
= -100 + (11)(2)
= -100 + 22
= -78
Therefore, the 12th term from the end is -78.
Q17: Which term of the AP: 53, 48, 43,... is the first negative term?
It is given that
AP: 53, 48, 43,…
First term (a) = 53 and
Common difference (d) = 48 - 53 = -5
Consider the nth term of the AP as the first negative term.
i.e., Tn < 0
We know that the nth term of an AP,
Tn = a + (n - 1)d
Here
⇒ [a + (n - 1 )d] < 0
Substituting the values
⇒ 53 + (n - 1)(-5) < 0
⇒ 53 - 5n + 5 < 0
So we get
⇒ 58 - 5n < 0
⇒ 5n > 58
⇒ n > 11.6
⇒ n = 12
So the 12th term is the first negative term of the given AP
T12 = a + (12 - 1)d
= 53 + 11 (-5)
= 53 - 55
= - 2 < 0
Therefore, the first negative term is the 12th term.
Q18: How many numbers lie between 10 and 300, which when divided by 4 leave a remainder 3.
The first number is 11, which divided by 4 leaves a remainder 3 between 10 and 300
The last term before 300 is 299, which is divided by 4 leave remainder 3.
So it is in an arithmetic progression as
11, 15, 19, 23, 299
First-term (a) = 11,
Common difference (d) = 15 - 11 = 4
We know that nth term,
an = a + (n - 1)d
Substituting the values
299 = 11 + (n - 1) 4
4(n - 1) = 288
So we get
(n - 1) = 72
n = 73
Therefore, 73 numbers lie between 10 and 300.
Q19: Find the sum of the two middlemost terms of the AP: -4/3, -1, -2/3,.........,4 ⅓
Given, the arithmetic series is -4/3, -1, -2/3,-------------,4 ⅓
We have to find the sum of the two middle most terms of the series.
From the given series,
First term, a = -4/3,
aₙ = 4 ⅓ = 13/3
Common difference, d = -1 - (-4/3)
= -1 + 4/3
= (-3+4)/3
d = 1/3
The n-th term of an AP is given by
aₙ = a + (n - 1)d
To find n,
13/3 = -4/3 + (n - 1)(1/3)
13/3 + 4/3 = (n - 1)(1/3)
17/3 = (1/3)(n - 1)
n - 1 = 17
n = 17 + 1
n = 18
The two middle most terms of the 18 terms of the series are 9th and 10th terms.
So, a₉ = -4/3 + (9 - 1)(1/3)
= -4/3 + (8/3)
= (-4+8)/3
a₉ = 4/3
a₁₀ = -4/3 + (10 - 1)(1/3)
= -4/3 + (9/3)
= (-4+9)/3
a₁₀ = 5/3
Now, sum of two middle terms = a₉ + a₁₀
= 4/3 + 5/3
= (4+5)/3
= 9/3
= 3
Therefore, the sum of the two middlemost terms of the given AP is 3.
Q20: The first term of an AP is –5 and the last term is 45. If the sum of the terms of the AP is 120, then find the number of terms and the common difference.
Given, the first term of an AP, a = -5
Last term of an AP, l = 45.
Sum of the term of the AP, S = 120
We have to find the number of terms and the common difference.
We know that, if l is the last term of an AP, then the sum of the terms is given by
S = n/2[a + l]
So, 120 = n/2[-5 + 45]
120 = n/2[40]
120 = 20n
n = 120/20
n = 6
The nth term of an AP is given by
aₙ = a + (n - 1)d
Given, a₆ = 45
45 = -5 + (6 - 1)d
45 + 5 = 5d
50 = 5d
d = 50/5
d = 10
Therefore, the number of terms is 6 and the common difference is 10.
Q21: Find the sum:
(i) 1 + (–2) + (–5) + (–8) + ... + (–236)
(ii) - 1/n + 4 - 2/n + 4 - 3/n +.....upto n terms
(iii) (a - b)/(a + b) + (3a - 2b)/(a + b) + (5a - 3b)/(a + b) to 11 terms
(i) 1 + (–2) + (–5) + (–8) + ... + (–236)
Given, the series is 1 + (-2) + (-5) + (-8) + ... + (-236)
We have to find the sum of the series.
From the given series,
First term, a= 1
Last term, n = -236
Common difference, d = -2 - 1 = -3
The nth term of the series in AP is given by
aₙ = a + (n - 1)d
-236 = 1 + (n - 1)(-3)
-236 - 1 = (n - 1)(-3)
n - 1 = 237/3
n - 1 = 79
n = 79 + 1
n = 80
We know that, if l is the last term of an AP, then the sum of the terms is given by
S = n/2[a+l]
So, S = 80/2[1 + (-236)]
= 40[-235]
= -9400
Therefore, the sum of the term is -9400.
(ii) - 1/n + 4 - 2/n + 4 - 3/n +.....upto n terms
Given, the series is 4 - 1/n + 4 - 2/n + 4 - 3/n +.....upto n terms.
We have to find the sum of the series upto n terms.
The given series can also be written as
4n - (1/n + 2/n, ………….+ n/n)
= 4n - (1 + 2 + 3 + .....+ n)/n
The sum of the first n natural numbers is given by
S = n(n + 1)/2
So, the series can be rewritten as
= 4n - n(n + 1)/2n
Cancelling out common term,
= 4n - (n + 1)/2
= 8n - n - 1/2
= (7n - 1)/2
Therefore, the sum of the term is (7n - 1)/2.
(ii) (a - b)/(a + b) + (3a - 2b)/(a + b) + (5a - 3b)/(a + b) to 11 terms
Given, the series is
We have to find the sum of the arithemtic series upto 11 terms.
From the given series,
First term, a = (a - b)/(a + b)
Common difference, d = (3a - 2b)/(a + b) - (a - b)/(a + b)
= (3a - 2b - a + b)/(a + b)
d = (2a - b)/(a + b)
The sum of the first n terms of an AP is given by
Sₙ = n/2[2a + (n - 1)d]
So, S₁₁ = (11/2)[2(a - b)/(a + b) + (11-1)(2a - b)/(a + b)]
= (11/2)[(2a - 2b)/(a + b) + (10)(2a - b)/(a + b)]
= (11/2)[(2a - 2b)/(a + b) + (20a - 10b)/(a + b)]
= (11/2)[2a - 2b + 20a - 10b]/(a + b)
= (11/2)/(a + b)[22a - 12b]
Taking out common term,
= (11/2)/(a + b)[2(11a - 6b)]
= (11/a + b)[11a - 6b]
= 11(11a - 6b)/(a+b)
Therefore, the sum of the series upto 11 terms is 11(11a - 6b)/(a + b)
Q22: Which term of the AP: –2, –7, –12,... will be –77? Find the sum of this AP upto the term –77.
Given, the series is -2, -7, -12,......., -77.
We have to find the sum up to the term -77.
From the series,
First term, a = -2
Last term, l = -77
Common difference, d = -7 - (-2) = -7 + 2 = -5
The nth term of the series in AP is given by
aₙ = a + (n - 1)d
So, -77 = -2 + (n - 1)(-5)
-77 + 2 = (n - 1)(-5)
75 = (n - 1)(5)
n - 1 = 75/5
n - 1 = 15
n = 15 + 1
n = 16
If l is the last term of an AP, then the sum of the terms is given by
S = n/2[a+l]
So, S = 16/2[-2 + (-77)]
S = 8[-2 - 77]
= 8(-79)
S = -632
Therefore, the sum of the term is -632.
Q23: If an = 3 – 4 n, show that a1 ,a2 , a3 , ... form an AP. Also find S20.
Given, aₙ = 3 - 4n
We have to show that the given expression forms an AP and find the sum up to 20 terms.
Put n =1, a₁ = 3 - 4(1) = 3 - 4 = -1
Put n= 2, a₂ = 3 - 4(2) = 3 - 8 = -5
Put n= 3, a₃ = 3 - 4(3) = 3 - 12 = -9
Put n= 4, a₄ = 3 - 4(4) = 3 - 16 = -13
Put n= 20, a₂₀ = 3 - 4(20) = 3 - 80 = -77
So, the series is -1, -5, -9, -13,........, -77.
First term, a = -1
Last term, l = -77
Common difference, d = -5 - (-1) = -5 + 1 = -4
To check whether the series form an AP,
Common difference, d = -5 - (-1) = -9 - (-5) = -13 - (-9)
d = -5 + 1 = -9 + 5 = -13 + 9 = -4
d = -4
It is clear that the series is in AP.
If l is the last term of an AP, then the sum of the terms is given by
S = n/2[a + l]
So, S = 20/2[-1 + (-77)]
= 10[-5-77]
= 10(-78)
= -780
Therefore, the sum of the series up to 20 terms is -780.
Q24: In an AP, if Sn = n (4n + 1), find the A.
Given, the expression for the sum of the terms is Sₙ = n(4n + 1)
We have to find the AP.
Put n = 1,
S₁ = 1(4(1) + 1) = 4 + 1 = 5
Put n =2,
S₂ = 2(4(2) + 1) = 2(8 + 1) = 2(9) = 18
The AP in terms of common difference is given by
a, a+d, a+2d, a+3d,......., a+(n-1)d
So, S₁ = a
First term, a = 5
S₂ = sum of first two terms of an AP
= a+ a + d
= 2a + d
To find the common difference d,
2a + d = 18
2(5) + d = 18
10 + d = 18
d = 18 - 10
d = 8
The series can be framed as
a = 5
a + d = 5 + 8 = 13
a + 2d = 5 + 2(8) = 5 + 16 = 21
a + 3d = 5 + 3(8) = 5 + 24 = 29
Therefore, the series is 5, 13, 21, 29,.....
Q25: In an AP, if Sn = 3 n2 + 5n and ak = 164, find the value of k.
Given, the expression for the sum of the series is Sₙ = 3n² + 5n
Last term, l is ak = 164
We have to find the value of k.
Put n = 1, S₁ = 3(1)² + 5(1) = 3 + 5 = 8
S₂ = 3(2)² + 5(2) = 3(4) + 10 = 12 + 10 = 22
The AP in terms of common difference is given by
a, a+d, a+2d, a+3d,......., a+(n - 1)d
So, S₁ = a
First term, a = 8
S₂ = sum of first two term of an AP
= a+ a + d
= 2a + d
To find the common difference d,
2a + d = 22
2(8) + d = 22
16 + d = 22
d = 22 - 16
d = 6
The series can be framed as
a = 8
a + d = 8 + 6 = 14
a + 2d = 8 + 2(6) = 8 + 12 = 20
a + 3d = 8 + 3(6) = 8 + 18 = 26
Therefore, the series is 8, 14, 20, 26,.....
The nth term of the series in AP is given by
aₙ = a + (n - 1)d
164 = 8 + (n - 1)(6)
164 - 8 = 6(n - 1)
n - 1 = 156/6
n - 1 = 26
n = 26 + 1
n = 27
Therefore, the value of k is 27.
Q26: If Sn denotes the sum of first n terms of an AP, prove that S12 = 3(S8 –S4)
Given, Sₙ denotes the sum of first n terms of an AP.
We have to prove that S₁₂ = 3(S₈ - S₄).
The sum of the first n terms of an AP is given by
Sₙ = (n/2)[2a + (n-1)d]
LHS: S₁₂
When n = 12, S₁₂ = (12/2)[2a + (12-1)d]
S₁₂ = 6[2a + 11d]
S₁₂ = 12a + 66d
RHS: 3(S₈ - S₄)
When n = 8, S₈ = (8/2)[2a + (8-1)d]
S₈ = 4[2a + 7d]
S₈ = 8a + 28d
When n = 4, S₄ = (4/2)[2a + (4-1)d]
S₄ = 2[2a + 3d]
S₄ = 4a + 6d
Now, S₈ - S₄ = (8a + 28d) - (4a + 6d)
= 8a + 28d - 4a - 6d
= 8a - 4a + 28d - 6
= 4a + 22d
3(S₈ - S₄) = 3(4a + 22d)
= 12a + 66d
= S₁₂
LHS = RHS
Therefore, it is proved that S₁₂ = 3(S₈ - S₄).
Q27: Find the sum of the first 17 terms of an AP whose 4th and 9th terms are –15 and –30 respectively.
Given, the 4-th term of an AP = -15
The 9-th term of an AP = -30
We have to find the first 17 terms of an AP.
The nth term of the series in AP is given by
aₙ = a + (n - 1)d
When n = 4, a₄ = a + (4 - 1) d
a + 3d = -15 --------------- (1)
When n = 9, a₉ = a + (9 - 1)d
a + 8d = -30 ----------------(2)
Subtracting (1) from (2),
a + 8d - (a + 3d) = -30 - (-15)
a + 8d - a - 3d = -30 + 15
8d - 3d = -15
5d = -15
d = -15/5
d = -3
Put d = -3 in (1),
a + 3(-3) = -15
a - 9 = -15
a = -15 + 9
a = -6
The sum of the first n terms of an AP is given by
Sₙ = n/2[2a + (n - 1)d]
To find the sum of the 17 terms,
S17 = 17/2[2(-6) + (17 - 1)(-3)]
= 17/2[-12 + (16)(-3)]
= 17/2[-12 - 48]
= 17/2[-60]
= 17(-30)
S17 = -510
Therefore, the sum of the first 17 terms is -510.
Q28: If the sum of first 6 terms of an AP is 36 and that of the first 16 terms is 256, find the sum of the first 10 terms.
Given, the sum of first 6 terms of an AP is 36
Also, the sum of the first 16 terms of an AP is 256.
We have to find the sum of the first 10 terms.
The sum of the first n terms of an AP is given by
Sₙ = n/2[2a + (n-1)d]
Where, a is the first term
n is the number of terms
d is the common difference
When n = 6,
S₆ = 6/2[2a + (6 - 1)d]
36 = 3[2a + 5d]
2a + 5d = 12 -------------------- (1)
When n = 16,
S₁₆ = 16/2[2a + (16 - 1)d]
256 = 8[2a + 15d]
2a + 15d = 32 ------------------- (2)
Subtracting (1) from (2),
2a + 15d - (2a + 5d) = 32 - 12
2a + 15d - 2a - 5d = 20
15d - 5d = 20
10d = 20
d = 20/10
d = 2
Put d = 2 in (1),
2a + 5(2) = 12
2a + 10 = 12
2a = 12 -10
2a = 2
a = 1
So, the first term, a = 1
Common difference, d = 2
Sum of the first 10 terms, S₁₀ = 10/2[2(1) + (10 - 1)(2)]
= 5[2 + 9(2)]
= 5[2 + 18]
= 5(20
= 100
Therefore, the sum of the first 10 terms of an AP is 100.
Q29: Find the sum of all the 11 terms of an AP whose middlemost term is 30.
Given, the middle term of an AP is 30.
We have to find the sum of all the 11 terms of an AP.
There are 11 terms in total. So, the middle term will be the 6th term.
The nth term of the series in AP is given by
aₙ = a + (n - 1)d
a + (6 - 1)d = 30
a + 5d = 30 ---------- (1)
The sum of the first n terms of an AP is given by
Sₙ = n/2[2a + (n-1)d]
The sum of the first 11 terms of the series is
S₁₁ = 11/2[2a + (11 - 1)d]
= 11/2[2a + 10d]
Taking out common term,
= (11/2)2[a + 5d]
Cancelling out common term,
S₁₁ = 11[a + 5d]--------- (2)
Substituting (1) in (2)
= 11(30)
= 330
Therefore, the sum of the first 11 terms of an AP is 330.
Q30: Find the sum of the last ten terms of the AP: 8, 10, 12,---, 126.
Given, the series in AP as 8, 10, 12, ………, 126.
We have to find the sum of the last 10 terms of the series.
From the series,
We need to find the sum of last 10 terms,
So, common difference, d = 8 -10 = -2
so we take the first term (a) as 126.
The sum of the first n terms of an AP is given by
Sₙ = n/2[2a + (n-1)d]
So, S₁₀ = 10/2[2(126) + (10 - 1)(-2)]
= 5[252 + 9(-2)]
= 5[252 - 18]
= 5[234]
= 1170
Therefore, the sum of the last 10 terms of an AP is 1170.
Q31: Find the sum of the first seven numbers which are multiples of 2 as well as of 9. [Hint: Take the LCM of 2 and 9]
Given, the series is a multiple of 2 as well as 9.
Also, take the LCM of 2 and 9.
We have to find the sum of the first seven numbers.
LCM of 2 and 9 is 18.
So, the series is a multiple of 18.
The first seven multiple of 18 are (18×1), (18×2), (18×3), (18×4), (18×5), (18×6), (18×7)
Therefore, the series is 18, 36, 54, 72, 90, 108, 126.
If l is the last term of an AP, then the sum of the terms is given by
S = n/2[a + l]
Here, first term, a = 18
Last term, l = 126
Common difference, d = 18
S = 7/2[18 + 126]
= 7/2[144]
= 7(72)
= 504
Therefore, the sum of the first seven numbers which are multiples of 2 as well as 9 is 504.
Q32: How many terms of the AP: –15, –13, –11,--- are needed to make the sum –55? Explain the reason for the double answer.
Given, the series in AP is -15, -13, -11,.......
We have to find the number of terms required to make the sum equal to -55.
From the series,
First term, a = -15
Common difference, d= -13 - (-15) = -13 + 15 = 2
The sum of the first n terms of an AP is given by
Sₙ = n/2[2a + (n - 1)d]
So, Sₙ = n/2[2(-15) + (n - 1)(2)]
= n/2[-30 + 2n - 2]
= n/2[2n -32]
= (n/2)2[n - 16]
= n(n - 16)
= n² - 16n
Given, the sum is -55
So, Sₙ = -55
n² - 16n + 55 = 0
On factoring,
n² - 11n - 5n + 55 = 0
n(n - 11)- 5(n - 11) = 0
(n - 5)(n - 11) = 0
Now, n - 5 = 0
n = 5
Also, n - 11 = 0
n = 11
Therefore, the sum of the first 5 terms or the sum of the first 11 terms of an AP is equal to -55.
The 11 terms of the series are -15, -13, -11, -9, -7, -5, -3, -1, 1, 3, 5.
The reason for the double answer is that the AP is increasing with positive values.
So, the sum of the first 5 terms will be equal to -55
As the AP increases with positive values the sum of the first 11 terms equals -55, as the last 6 terms sum up to 0.
Q33: The sum of the first n terms of an AP whose first term is 8 and the common difference is 20 is equal to the sum of first 2n terms of another AP whose first term is – 30 and the common difference is 8. Find n.
Given,
The sum of first n terms of an AP is equal to the sum of first 2n terms of another AP.
We have to find the value of n.
given, the first AP series have
First term, a = 8
Common difference, d = 20
Also, the second AP series have
First term, a = -30
Common difference, d = 8
The sum of the first n terms of an AP is given by
Sₙ = n/2[2a + (n - 1)d]
For the first series, Sₙ = n/2[2(8) + (n - 1)(20)]
= n/2[16 + 20n - 20]
= n/2[20n - 4]
Taking out common term,
= (n/2)2[10n - 2]
Cancelling out common term,
Sₙ = n[10n - 2]
For the second series, S₂ₙ = (2n/2)[2(-30) + (2n - 1)(8)]
= n[-60 + 16n - 8]
S₂ₙ = n[16n - 68]
Given, Sₙ = S₂ₙ
n[10n - 2] = n[16n - 68]
10n - 2 = 16n - 68
10n - 16n = -68 + 2
-6n = -66
n = 66/6
n = 11
Therefore, the value of n is 11.
Q34: Kanika was given her pocket money on Jan 1st, 2008. She puts Re 1 on Day 1, Rs 2 on Day 2, Rs 3 on Day 3, and continued doing so till the end of the month, from this money into her piggy bank. She also spent Rs 204 of her pocket money and found that at the end of the month she still had Rs 100 with her. How much was her pocket money for the month?
It is stated that Kanika was given pocket money on Jan 1st 2008.
She put Re.1 on day 1, Rs.2 on day 2, Rs.3 on day, and so on into her piggy bank till the end of the month.
We have to find the amount of pocket money for the month.
January has 31 days.
So, the series will be 1, 2, 3, ……….,31.
From the series,
First term, a = 1
Last term, l = 31
Common difference, d = 2 -1 = 1
If l is the last term of an AP, then the sum of the terms is given by
S = n/2[a + l]
Here, n = 31
So, S = 31/2[1 + 31]
= 31/2[32]
= 31(16)
S = 496
Given, Rs. 204 from the pocket money was spent by Kanika.
After spending the amount of money left in the piggy bank is Rs.100.
Kanika’s total pocket money = 496 + 204 + 100
= 496 + 304
= 800
Therefore, the total pocket money is Rs.800.
Q35: Yasmeen saves Rs. 32 during the first month, Rs. 36 in the second month and Rs. 40 in the third month. If she continues to save in this manner, in how many months will she save Rs. 2000?
Given, Yasmeen saves Rs 32 in the first month, Rs 36 in the second month and Rs 40 in the third month.
We have to find how many months it will take to save in this manner upto Rs 2000.
The series is 32, 36, 40,.....
Common difference, d = 36 - 32 = 4
First term, a = 32
Sum = 2000
The sum of the first n terms of an AP is given by
Sₙ = n/2[2a + (n-1)d]
So, 2000 = n/2[2(32) + (n - 1)(4)]
2000 = n/2[64 + 4n - 4]
4000 = n[4n + 60]
4n² + 60n = 4000
4n² + 60n - 4000 = 0
Dividing by 4,
n² + 15n - 1000 = 0
On factoring,
n² + 40n - 25n - 1000 = 0
n(n + 40) - 25(n + 40) = 0
(n - 25)(n + 40) = 0
Now, n - 25 = 0
n = 25
Also, n + 40 = 0
n = -40
Since a negative value is not possible, n = -40 is neglected.
Therefore, the number of months required to save upto Rs.2000 is 25.
Exercise 5.4
Q1: The sum of the first five terms of an AP and the sum of the first seven terms of the same AP is 167. If the sum of the first ten terms of this AP is 235, find the sum of its first twenty terms.
We know that, in an A.P.,
First term = a
Common difference = d
Number of terms of an AP = n
According to the question,
We have,
S5 + S7 = 167
Using the formula for sum of n terms,
Sn = (n/2) [2a + (n-1)d]
So, we get,
(5/2) [2a + (5-1)d] + (7/2)[2a + (7-1)d] = 167
5(2a + 4d) + 7(2a + 6d) = 334
10a + 20d + 14a + 42d = 334
24a + 62d = 334
12a + 31d = 167
12a = 167 – 31d …(1)
We have,
S10 = 235
(10/2) [2a + (10-1)d] = 235
5[ 2a + 9d] = 235
2a + 9d = 47
Multiplying L.H.S and R.H.S by 6,
We get,
12a + 54d = 282
From equation (1)
167 – 31d + 54d = 282
23d = 282 – 167
23d = 115
d = 5
Substituting the value of d = 5 in equation (1)
12a = 167 – 31(5)
12a = 167 – 155
12a = 12
a = 1
We know that,
S20 = (n/2) [2a + (20 – 1)d]
= 20/(2[2(1) + 19 (5)])
= 10[ 2 + 95]
= 970
Therefore, the sum of first 20 terms is 970.
Q2: Find the
(i) Sum of those integers between 1 and 500 which are multiples of 2 as well as of 5.
(ii) Sum of those integers from 1 to 500 which are multiples of 2 as well as of 5.
(iii) Sum of those integers from 1 to 500 which are multiples of 2 or 5.
[Hint (iii): These numbers will be: multiples of 2 + multiples of 5 – multiples of 2 as well as of 5]
Sol: (i) Sum of those integers between 1 and 500 which are multiples of 2 as well as of 5.
We know that,
Multiples of 2 as well as of 5 = LCM of (2, 5) = 10
Multiples of 2 as well as of 5 between 1 and 500 = 10, 20, 30…, 490.
Hence,
We can conclude that 10, 20, 30…, 490 is an AP with common difference, d = 10
First term, a = 10
Let the number of terms in this AP = n
Using nth term formula,
an = a + (n – 1)d
490 = 10 + (n – 1)10
480 = (n – 1)10
n – 1 = 48
n = 49
Sum of an AP,
Sn = (n/2) [a + an], here an is the last term, which is given]
= (49/2) × [10 + 490]
= (49/2) × [500]
= 49 × 250
= 12250
Therefore, sum of those integers between 1 and 500 which are multiples of 2 as well as of 5 = 12250
(ii) Sum of those integers from 1 to 500 which are multiples of 2 as well as of 5.
We know that,
Multiples of 2 as well as of 5 = LCM of (2, 5) = 10
Multiples of 2 as well as of 5 from 1 and 500 = 10, 20, 30…, 500.
Hence,
We can conclude that 10, 20, 30…, 500 is an AP with common difference, d = 10
First term, a = 10
Let the number of terms in this AP = n
Using nth term formula,
an = a + (n – 1)d
500 = 10 + (n – 1)10
490 = (n – 1)10
n – 1 = 49
n = 50
Sum of an AP,
Sn = (n/2) [ a + an], here an is the last term, which is given]
= (50/2) ×[10 + 500]
= 25× [10 + 500]
= 25(510)
= 12750
Therefore, sum of those integers from 1 to 500 which are multiples of 2 as well as of 5= 12750
(iii) Sum of those integers from 1 to 500 which are multiples of 2 or 5.
We know that,
Multiples of 2 or 5 = Multiple of 2 + Multiple of 5 – Multiple of LCM (2, 5)
Multiples of 2 or 5 = Multiple of 2 + Multiple of 5 – Multiple of LCM (10)
Multiples of 2 or 5 from 1 to 500 = List of multiple of 2 from 1 to 500 + List of multiple
of 5 from 1 to 500 – List of multiple of 10 from 1 to 500
= (2, 4, 6… 500) + (5, 10, 15… 500) – (10, 20, 30… 500)
Required sum = sum(2, 4, 6,…, 500) + sum(5, 10, 15,…, 500) – sum(10, 20, 30,., 500)
Consider the first series,
2, 4, 6, …., 500
First term, a = 2
Common difference, d = 2
Let n be no of terms
an = a + (n – 1)d
500 = 2 + (n – 1)2
498 = (n – 1)2
n – 1 = 249
n = 250
Sum of an AP, Sn = (n/2) [ a + an]
Let the sum of this AP be S1,
S1 = S250 = (250/2) ×[2 + 500]
S1 = 125(502)
S1 = 62750 … (1)
Consider the second series,
5, 10, 15, …., 500
First term, a = 5
Common difference, d = 5
Let n be no of terms
By nth term formula
an = a + (n – 1)d
500 = 5 + (n – 1)
495 = (n – 1)5
n – 1 = 99
n = 100
Sum of an AP, Sn = (n/2) [ a + an]
Let the sum of this AP be S2,
S2 = S100 = (100/2) ×[5 + 500]
S2 = 50(505)
S2 = 25250 … (2)
Consider the third series,
10, 20, 30, …., 500
First term, a = 10
Common difference, d = 10
Let n be no of terms
an = a + (n – 1)d
500 = 10 + (n – 1)10
490 = (n – 1)10
n – 1 = 49
n = 50
Sum of an AP, Sn = (n/2) [ a + an]
Let the sum of this AP be S3,
S3 = S50 = (50/2) × [2 + 510]
S3 = 25(510)
S3 = 12750 … (3)
Therefore, the required Sum, S = S1 + S2 – S3
S = 62750 + 25250 – 12750
= 75250
Q3: The eighth term of an AP is half its second term and the eleventh term exceeds one third of its fourth term by 1. Find the 15th term.
We know that,
First term of an AP = a
Common difference of AP = d
nth term of an AP, an = a + (n – 1)d
According to the question,
as = ½ a2
2a8 = a2
2(a + 7d) = a + d
2a + 14d = a + d
a = – 13d …(1)
Also,
a11 = 1/3 a4 + 1
3(a + 10d) = a + 3d + 3
3a + 30d = a + 3d + 3
2a + 27d = 3
Substituting a = -13d in the equation,
2 (- 13d) + 27d = 3
d = 3
Then,
a = – 13(3)= – 39
Now,
a15 = a + 14d
= – 39 + 14(3)
= – 39 + 42
= 3
So 15th term is 3.
Q4: An AP consists of 37 terms. The sum of the three middlemost terms is 225 and the sum of the last three is 429. Find the AP.
We know that,
First term of an AP = a
Common difference of AP = d
nth term of an AP, an = a + (n – 1)d
Since, n = 37 (odd),
Middle term will be (n+1)/2 = 19th term
Thus, the three middle most terms will be,
18th, 19th and 20th terms
According to the question,
a18 + a19 + a20 = 225
Using an = a + (n – 1)d
a + 17d + a + 18d + a + 19d = 225
3a + 54d = 225
3a = 225 – 54d
a = 75 – 18d … (1)
Now, we know that last three terms will be 35th, 36th and 37th terms.
According to the question,
a35 + a36 + a37 = 429
a + 34d + a + 35d + a + 36d = 429
3a + 105d = 429
a + 35d = 143
Substituting a = 75 – 18d from equation 1,
75 – 18d + 35d = 143 [ using eqn1]
17d = 68
d = 4
Then,
a = 75 – 18(4)
a = 3
Therefore, the AP is a, a + d, a + 2d….
i.e. 3, 7, 11….
Q5: Find the sum of the integers between 100 and 200 that are
(i) divisible by 9
(ii) not divisible by 9
[Hint (ii): These numbers will be: Total numbers – Total numbers divisible by 9]
(i) The number between 100 and 200 which is divisible by 9 = 108, 117, 126, …198
Let the number of terms between 100 and 200 which is divisible by 9 = n
an = a + (n – 1)d
198 = 108 + (n – 1)9
90 = (n – 1)9
n – 1 = 10
n = 11
Sum of an AP = Sn = (n/2) [ a + an]
Sn = (11/2) × [108 + 198]
= (11/2) × 306
= 11(153)
= 1683
(ii) Sum of the integers between 100 and 200 which is not divisible by 9 = (sum of total numbers between 100 and 200) – (sum of total numbers between 100 and 200 which is divisible by 9)
Sum, S = S1 – S2
Here,
S1 = sum of AP 101, 102, 103, – – – , 199
S2 = sum of AP 108, 117, 126, – – – , 198
For AP 101, 102, 103, – – – , 199
First term, a = 101
Common difference, d = 199
Number of terms = n
Then,
an = a + (n – 1)d
199 = 101 + (n – 1)1
98 = (n – 1)
n = 99
Sum of an AP = Sn = (n/2) [ a + an]
Sum of this AP,
S1 = (99/2) × [199 + 101]
= (99/2) × 300
= 99(150)
= 14850
For AP 108, 117, 126, – – – – , 198
First term, a = 108
Common difference, d = 9
Last term, an = 198
Number of terms = n
Then,
an = a + (n – 1)d
198 = 108 + (n – 1)9
10 = (n – 1)
n = 11
Sum of an AP = Sn = (n/2) [ a + an]
Sum of this AP,
S2 = (11/2) × [108 + 198]
= (11/2) × (306)
= 11(153)
= 1683
Substituting the value of S1 and S2 in the equation, S = S1 – S2
S = S1 + S2
= 14850 – 1683
= 13167
Q6: The ratio of the 11th term to the 18th term of an AP is 2 : 3. Find the ratio of the 5th term to the 21st term, and also the ratio of the sum of the first five terms to the sum of the first 21 terms.
Given, the ratio of 11th term to the 18th term of an AP is 2:3
We have to find
(A) the ratio of the 5th term to the 21st term.
(B) the ratio of the sum of the first five terms to the sum of the first 21 terms.
The nth term of the series in AP is given by
aₙ = a + (n - 1)d
11th term = a + (11-1)d = a + 10d
18th term = a + 17d
As per given condition, 11th term/18th term = 2/3
(a+10d)/(a+17d) = 2/3
3(a+10d) = 2(a+17d)
3a + 30d = 2a + 34d
By grouping,
3a - 2a = 34d - 30d
a = 4d ------------------------ (1)
(A) to find the ratio of the 5th term to the 21st term
5th term = a + 4d
21st term = a + 20d
(a + 4d) /(a + 20d)
Substitute (1) in the above expression,
(4d+4d)/(4d+20d)
= 8d/24d
= 1/3
Therefore, the ratio of the 5th term to the 21st term is 1:3
(B) the ratio of the sum of the first 5 terms to the sum of the first 21 terms.
The sum of the first n terms of an AP is given by
Sₙ = n/2[2a + (n-1)d]
The sum of first five terms is S₅ = 5/2[2a + (5 - 1)d]
S₅ = 5/2[2a + 4d]
S₅ = (5/2)2[a + 2d]
S₅ = 5a + 10d
The sum of first 21 terms is S₂₁ = 21/2[2a + (21 - 1)d]
S₂₁ = 21/2[2a + 20d]
S₂₁ = (21/2)2[a + 10d]
S₂₁ = 21a + 210d
As per given condition, S₅/S₂₁
= (5a+10d)/((21a+210d)
Substitute (1) in the above expression,
= (5(4d) + 10d)/(21(4d) + 210d)
= (20d+10d)/(84d+210d)
= 30d/294d
= 5/49
Therefore, the ratio of the sum of the first 5 terms to the sum of the first 21 terms is 5:49
Q7: Show that the sum of an AP whose first term is a, the second term b and the last term c, is equal to 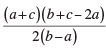 .
.
Given, the AP is a, b, c,.....
We have to prove that the sum of the AP is equal to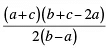
The nth term of the series in AP is given by
aₙ = a + (n - 1)d
Here, first term, a = a
Last term, l = c
Common difference, d = b - a
So, c = a + (n - 1)(b - a)
c - a = (n - 1)(b - a)
n - 1 = (c - a)/(b - a)
n = [(c - a)/(b - a)] + 1
If l is the last term of an AP, then the sum of the terms is given by
S = n/2[a+l]
So, S = ([(c - a)/(b - a)] + 1)/2[a + c]
= ((c - a)+(b - a)[a + c])/2(b - a)
= (c - a + b - a)(a + c)/2(b - a)
S =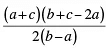
Hence proved.
Q8: Solve the equation – 4 + (–1) + 2 +...+ x = 437.
Given, the series is -4, -1, 2, ……, x
We have to find the value of x.
Here, first term, a = -4
Last term, l = x
Sum of the series, S = 437
Common difference, d = -1 - (-4) = -1 + 4 = 3
The nth term of the series in AP is given by
aₙ = a + (n - 1)d
So, x = -4 + (n - 1)3
x = -4 + 3n -3
x = 3n - 7
3n = x + 7
n = (x + 7)/3
If l is the last term of an AP, then the sum of the terms is given by
S = [n/2][a+l]
So, S = [(x + 7)/6][(-4 + x)]
437 = [(x + 7)(x - 4)]/6
437(6) = (x² + 7x - 4x - 28)
x² + 3x - 28 = 2622
x² + 3x - 2650 = 0
On factoring,
x² + 53x - 50x - 2650 = 0
x(x + 53) - 50(x + 53) = 0
(x - 50)(x + 53) = 0
Now, x + 53 = 0
x = -53
Also, x - 50 = 0
x = 50
Since a negative integer is not possible, x = -53 is neglected.
Therefore, the value of x is 50.
Q9: Jaspal Singh repays his total loan of Rs. 118000 by paying every month starting with the first instalment of Rs. 1000. If he increases the instalment by Rs. 100 every month, what amount will be paid by him in the 30th instalment? What amount of loan does he still have to pay after the 30th instalment?
Given, Jaspal Singh repays his total loan of Rs. 118000.
Monthly instalment is Rs. 1000.
We have to find the amount of loan he still have to pay after the 30th instalment, if he increases the instalment by Rs.100
Here, first term, a = 1000
Common difference, d = 100
To find a30,
The nth term of the series in AP is given by
an = a + (n - 1)d
So, a30 = 1000 + (30 - 1)(100)
= 1000 + 29(100)
= 1000 + 2900
a30 = 3900
So, the amount paid by Jaspal Singh in 30 instalments = Rs.3900
Loan amount paid in 30 instalments = S30
The sum of the first n terms of an AP is given by
Sn = n/2[2a + (n - 1)d]
So, S30 = 30/2[2(1000) + (30 - 1)(100)]
= 15[2000 + 2900]
= 15(4900)
S30 = Rs.73500
Amount of loan to be paid after 30 instalments = (total loan) - (loan amount paid for 30 instalments)
= 118000 - 73500
= Rs.44500
Therefore, the amount of loan to be paid by Jaspal Singh after 30 instalments is Rs. 44500.
Q10: The students of a school decided to beautify the school on the Annual Day by fixing colourful flags on the straight passage of the school. They have 27 flags to be fixed at intervals of every 2 m. The flags are stored at the position of the middlemost flag. Ruchi was given the responsibility of placing the flags. Ruchi kept her books where the flags were stored. She could carry only one flag at a time. How much distance did she cover in completing this job and returning back to collect her books? What is the maximum distance she travelled carrying a flag?
Given, the students decided to fix colourful flags on the straight passage of the school.
Also, there are 27 flags which are to be fixed at intervals of every 2 m.
We have to find the maximum distance she travelled carrying a flag.
The flags are stored at the position of the middle most flag.
Ruchi kept her books where the flags were stored.
Ruchi could carry only one flag at a time.
Here, number of flags, n = 27
The middle flag post is at (n + 1)/2 = (27 + 1)/2 = 28/2 = 14th post
Let us consider that Ruchi first fixes 13 flags on the left side and then completes fixing 13 flags on the right side.
From the middle post she carries one flag to 2m, fixes it and then returns 2m to the middle post.
So, she travels 2 + 2 = 4 m
Similarly, to fix the second flag she travels 4 + 4 = 8 m
To fix the third flag she travels 8 + 4 = 12 m
So, this forms a series
The series is 4, 8, 12, 16,......
Here, first term, a = 4
Common difference, d = 4
Number of flags, n = 13
The sum of the first n terms of an AP is given by
Sn = n/2[2a + (n - 1)d]
So, S = 13/2[2(4) + (13 - 1)(4)]
= 13/2[8 + 12(4)]
= 13/2[8 + 48]
= 13/2[56]
= 13(28)
= 364 m
So, she travels 364 m to fix flags on the left of the middle post.
So, total distance travelled by her to fix all the flags = 2(364) = 728 m.
Now, the distance travelled by Ruchi carrying the flag
= 728/2
= 364 m
Therefore, the maximum distance travelled by Ruchi carrying the flag is 364 m.
|
127 videos|584 docs|79 tests
|
FAQs on NCERT Exemplar: Arithmetic Progressions - Mathematics (Maths) Class 10
| 1. What is an arithmetic progression? |  |
| 2. How can the nth term of an arithmetic progression be calculated? |  |
| 3. How can we find the sum of the first 'n' terms of an arithmetic progression? |  |
| 4. Can an arithmetic progression have a negative common difference? |  |
| 5. What is the difference between an arithmetic progression and a geometric progression? |  |