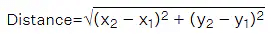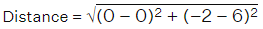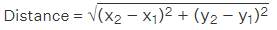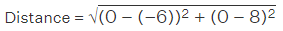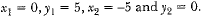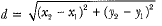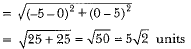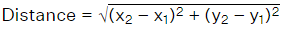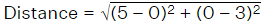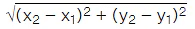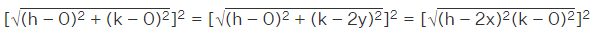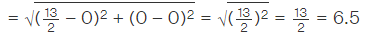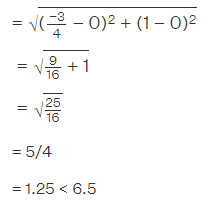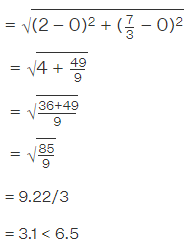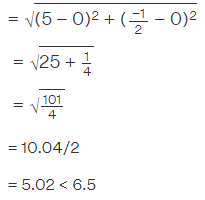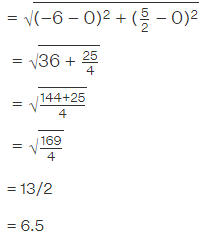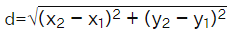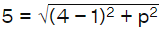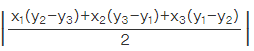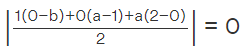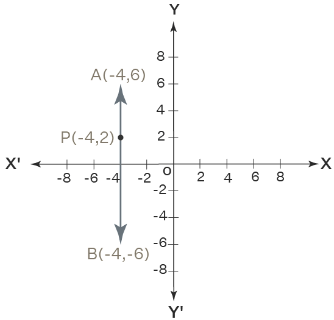NCERT Exemplar: Coordinate Geometry - 1 | Mathematics (Maths) Class 10 PDF Download
EXERCISE 7.1
Choose the correct answer from the given four options:
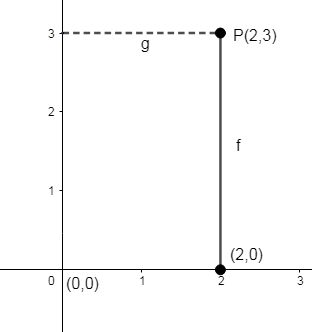
Q1: The distance of the point P (2, 3) from the x-axis is
(a) 2
(b) 3
(c) 1
(d) 5
Correct Answer is Option (b)
Let us mark the point P (2, 3) in the Cartesian plane.
The shortest distance between the coordinate (2, 3) and the x – axis is a straight line to the point (2, 0).
We are said to find the shortest distance from (x - axis). So the point is (2, 0).To find the distance, we can use the distance formula.
Distance formula
= √[(x2 - x1)² + (y2 - y1)²]
Here, (x1, y1) = (2,0), (x2, y2) = (2,3)
= √[(2 - 2)² + (3 - 0)²]
= √[0 + 9] = √9
= 3
Thus the shortest distance of the point P (2, 3) to the x – axis is 3 units.
∴ Option (b) is the correct answer.
Q2: The distance between the points A (0, 6) and B (0, –2) is
(a) 6
(b) 8
(c) 4
(d) 2
Correct Answer is Option (b)
We know that the formula to find the distance between two points A(x₁, y₁) and B(x₂, y₂) is
It is given that
We have to find the distance between the points A (0, 6) and B (0, –2)
Substituting these values in the equation we get
So we get
Distance between A and B = √64
Distance between A and B = 8 units
Therefore, the distance between the points A and B is 8 units.
Q3: The distance of the point P (–6, 8) from the origin is
(a) 8
(b) 2√7
(c) 10
(d) 6
Correct Answer is Option (c)
We know that the formula to find the distance between two points P(x₁, y₁) and Q(x₂, y₂) is
It is given thatWe have to find the distance of the point P (-6, 8) from origin i.e. (0, 0)
Substituting these values in the equation we get
So we getDistance of point P = √(36 + 64) = √100 = 10
Distance of point P = 10 units
Therefore, the distance of the point P (–6, 8) from the origin is 10 units.
Q4: Find distance between the points (0, 5) and (- 5, 0).
(a) 5
(b) 5√2
(c) 2√5
(d) 10
Correct Answer is Option (b)
Here
∴
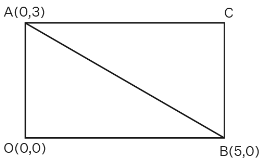
Q5: AOBC is a rectangle whose three vertices are A (0, 3), O (0, 0) and B (5, 0). Find the length of its diagonal.
(a) 5
(b) 3
(c) √34
(d) 4
Correct Answer is Option (c)
It is given that
AOBC is a rectangle whose three vertices are vertices A (0, 3), O (0, 0) and B (5, 0)Length of diagonal AB is the distance between the points (0,3) and (5,0)
We know that the formula to find the distance between two points P(x₁, y₁) and Q(x₂, y₂) is
Distance between the points (0,3) and (5,0) can be found by
So we get
Distance between the points = √(25 + 9) = √34
Distance between the points = √34 units
Therefore, the length of its diagonal is √34 units.
Q6: The perimeter of a triangle with vertices (0, 4), (0, 0) and (3, 0) is
(a) 5
(b) 12
(c) 11
(d) 7 + √5
Correct Answer is Option (b)
First find length of each sides of ∆
Let A( 4 , 0) B(0, 0) and C (0 , 3) be the vertices of the triangle.
Using distance formula we have
AB = √(42 + 0) = 4BC = √(0 + 32) = 3
CA = √(42 + 32) = 5
Clearly adding AB + BC + CA = perimeter of ∆
⇒ Perimeter of ∆ ABC = 3 + 4 + 5= 12 units
Q7: The area of a triangle with vertices A (3, 0), B (7, 0) and C (8, 4) is
(a) 14
(b) 28
(c) 8
(d) 6
Correct Answer is Option (c)
The vertices of the triangle are
A (3, 0), B (7, 0) and C (8, 4)
The formula to find the area of a triangle is
Area = 1/2 [x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)]
Substituting the values
Area = 1/2 [3(0 - 4) + 7(4 - 0) + 8(0 - 0)]
By further calculation
Area = 1/2 [3(-4) + 7(4) + 8(0)]Area = 1/2 [-12 + 28]
So we get
Area = 1/2 [16]
Area = 8 sq. units
Therefore, the area of a triangle is 8 sq. units.
Q8: The points (–4, 0), (4, 0), (0, 3) are the vertices of a
(a) right triangle
(b) isosceles triangle
(c) equilateral triangle
(d) scalene triangle
Correct Answer is Option (b)
Consider A(-4, 0), B(4, 0), C(0, 3) as the vertices givenDistance Formula:
Distance = √((x2 - x1)2 + (y2 - y1)2)
Now, Distance between A and B:
AB = √((4 - (-4))2 + (0 - 0)2)
AB = √64 = 8
Distance between B and C:
BC = √((0 - 4)2 + (3 - 0)2)
BC = √25 = 5
Distance between A and C:
AC = √((0 - (-4))2 + (3 - 0)2)
AC = √25 = 5
As BC = AC the triangle is isosceles
Therefore, the points are the vertices of an isosceles triangle.
Q9: The point which divides the line segment joining the points (7, –6) and (3, 4) in ratio 1 : 2 internally lies in the
(a) I quadrant
(b) II quadrant
(c) III quadrant
(d) IV quadrant
Correct Answer is Option (d)
We know that
m₁x₂ + m₂x₁m₁ + m₂, m₁y₂ + m₂y₁m₁ + m₂
Given:
(x1, y1) = (7, -6)
(x2, y2) = (3, 4)
m1 = 1
m2 = 2
Substituting the values in the section formula:
= 1 × 3 + 2 × 71 + 2, 1 × 4 + 2 × (-6)1 + 2
= 173, -83
As the x coordinate is positive and y coordinate is negative.
The point lies in the IV quadrant.
Q10: The point which lies on the perpendicular bisector of the line segment joining the points A (–2, –5) and B (2, 5) is
(a) (0, 0)
(b) (0, 2)
(c) (2, 0)
(d) (–2, 0)
Correct Answer is Option (a)
We know that
The coordinates of the mid-point of the line segment joining the point P (x1, y1) and Q (x2, y2) are [(x1 + x2)/2, (y1 + y2)/2]
The points given are A (-2, -5) and B (2, 5)Now by substituting the values in the formula
= [(-2 + 2)/2, (-5 + 5)/2]
= (0/2, 0/2)
= (0, 0)
Therefore, the point which lies on the perpendicular is (0, 0).
Q11: The fourth vertex D of a parallelogram ABCD whose three vertices are A (–2, 3), B (6, 7) and C (8, 3) is
(a) (0, 1)
(b) (0, –1)
(c) (–1, 0)
(d) (1, 0)
Correct Answer is Option (b)
Consider the fourth vertex as D = (x, y)
As the diagonals of a parallelogram bisect each other, the midpoint of AC is the same as the midpoint of BD.
We know that
The coordinates of the mid-point of the line segment joining the point are
[(x1 + x2)/2, (y1 + y2)/2]
As the midpoint of AC = Midpoint of BD
[(-2 + 8)/2, (3 + 3)/2] = [(6 + x)/2, (7 + y)/2]
By further calculation[6/2, 6/2] = [(6 + x)/2, (7 + y)/2]
Now we get
6 + x = 6
x = 6 - 6 = 0
And 7 + y = 6
y = 6 - 7 = -1
Therefore, the fourth vertex D is (0, -1).
Q12: If the point P (2, 1) lies on the line segment joining points A (4, 2) and B (8, 4), then
(a) AP = 1/3AB
(b) AP = PB
(c) PB = 1/3AB
(d) AP = 1/2AB
Correct Answer is Option (d)
We know that
The coordinates of the point (x, y) which divides the line segment joining the points (x1, y1) and (x2, y2) internally in the ratio m₁: m₂ are
(x, y) = m₁x₂ + m₂x₁m₁ + m₂, m₁y₂ + m₂y₁m₁ + m₂Consider P to divide AB in the ratio k:1
Let us substitute the values (x1, y1) = (4,2) and (x2, y2) = (8,4)
P = k(8) + 1(4)k + 1, k(4) + 1(2)k + 1
It is given that P = (2,1)
P = 8k + 4k + 1, 4k + 2k + 1 = (2,1)
Let us compare the x coordinates
(8k + 4)/ (k + 1) = 2
By cross multiplication
8k + 4 = 2k + 2
6k = -2
Divide both sides by -2
k = -1/3
As k value is negative, P divides AB in the ratio 1:3 externally
AP/PB = 1/3
AP = 1/2 AB
Therefore, the line segment joining points A (4, 2) and B (8, 4), then AP = 1/2 AB.
Q13: If P a/3, 4 is the mid-point of the line segment joining the points Q (– 6, 5) and R (– 2, 3), then the value of a is
(a) -4
(b) -12
(c) 12
(d) -6
Correct Answer is Option (d)
It is given that
P is the mid-point of the line segment QR
Px = a/3 = (-6 - 2)/2
By cross multiplication we get
2a = -24
Dividing both sides by 2
a = -12
Therefore, the value of a is -12.
Q14: The perpendicular bisector of the line segment joining the points A (1, 5) and B (4, 6) cuts the y-axis at
(a) (0, 13)
(b) (0, –13)
(c) (0, 12)
(d) (13, 0)
Correct Answer is Option (a)
The points given are
A(x₁, y₁) = (1, 5)
B(x₂, y₂) = (4, 6)
Perpendicular bisector of AB will pass through the mid-point of AB
Perpendicular bisector of AB will meet the Y axis at P(0, y)
AP = BP
We know that
The distance between two points P(x₁, y₁) and Q(x₂, y₂) is
Let us apply the distance formula
AP2 = BP2
(x1 - 0)2 + (y1 - y)2 = (x2 - 0)2 + (x2₂ - y)2
Substituting the values
(1- 0)2 + (5 - y)2 = (4 - 0)2 + (6 - y)2
Let us expand using (a - b)2 = a2 + b2 - 2ab
1 + 25 + y2 - 10y = 16 + 36 + y2- 12y
By further calculation
26 + y2 - 10y = 52 + y2 - 12y
So we get
y2 - 10y - y2 + 12y + 26 - 52 = 0
2y - 26 = 0
2y = 26
Divide both sides by 2
y = 13
Therefore, the perpendicular bisector of the line segment is (0, 13).
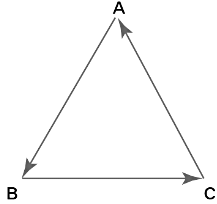
Q15: The coordinates of the point which is equidistant from the three vertices of the ∆ AOB as shown in the figure is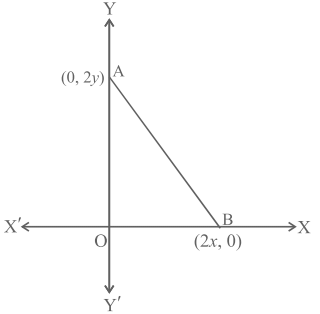
(a) (x, y)
(b) (y, x)
(c) x/2, y/2
(d) y/2, x/2
Correct Answer is Option (a)
Consider the coordinate of the point which is equidistant from the three vertices O (0, 0), A (0,
2y) and B (2x, 0) as P (h, k)
Here PO = PA = PBPO2 = PA2 = PB2 --- (1)
Now we get
h2 + k2 = h2 + (k - 2y)2 = (h - 2x)2 + k2 --- (1)
Let us consider the first two equation
h2 + k2 = h2 + (k - 2y)2
k2 = k2 + 4y2 - 4yk
Taking out the common terms
4y(y - k) = 0
y = k where y ≠ 0
Considering the first and third equationh2 + k2 = (h - 2x)2 + k2
h2 = h2 + 4x2 - 4xh
Taking out the common terms
4x(x - h) = 0
x = h where x ≠ 0
So the required points are (h, k) = (x, y)
Therefore, the coordinates of the point are (x, y).
Q16: A circle drawn with origin as the centre passes through (13/2,0). The point which does not lie in the interior of the circle is
(a) -3/4, 1
(b) 2.7/3
(c) 5,-1/3
(d) -6,5/2
Correct Answer is Option (d)
It is given that
A circle is drawn with origin as centre (0, 0) passes through (13/2, 0)
We know that
Radius of the circle = Distance between the two points
A point lies inside, on or outside the circle if the distance of the point from the centre of the circle is less than, equal to or greater than the radius of the circle.
Let us now check the options one by one
a. The distance between (0, 0) and (-3/4, 1)
(-3/4, 1) lies in the interior of the circle.
b. The distance between (0, 0) and (2, 7/3)
(2, 7/3) lies in the interior of the circle.
c. The distance between (0, 0) and (5, -1/2)
(5, -1/2) lies in the interior of the circle.
d. The distance between (0, 0) and (-6, 5/2)(-6, 5/2) lies on the circle.
Therefore, the point (-6, 5/2) does not lie in the interior of the circle.
Q17: A line intersects the y-axis and x-axis at the points P and Q, respectively. If
(2, –5) is the mid-point of PQ, then the coordinates of P and Q are, respectively
(a) (0, – 5) and (2, 0)
(b) (0, 10) and (– 4, 0)
(c) (0, 4) and (– 10, 0)
(d) (0, – 10) and (4, 0)
Correct Answer is Option (d)
We know that
The coordinates of the mid-point of the line segment joining the point are
[(x1 + x2)/2, (y1 + y2)/2]
Consider the coordinates of P as (x, y) and Q as (x2, y2)
The midpoint of PQ = (2, -5)
Using the midpoint formula
x = (x1 + x2)/2 and y = (y1 + y2)/2
2 = (x1 + x2)/2 and -5 = (y1 + y2)/2
By cross multiplication
x1 + x2 = 4
y1 + y2 = -10
As the line PQ intersects the Y-axis at P
x1 = 0
In the same way, y2 = 0
x2 = 4 and y1 = -10
So the coordinates of P is (0, -10) and Q is (4, 0).
Therefore, the coordinates of P and Q are (0, -10) and (4, 0).
Q18: The area of a triangle with vertices (a, b + c), (b, c + a) and (c, a + b) is
(a) (a + b + c)2
(b) 0
(c) a + b + c
(d) abc
Correct Answer is Option (b)
Consider the vertices of a triangle as
A = (x₁, y₁) = (a, b + c)
B = (x₂, y₂) = (b, c + a)
C = (x₃, y₃) = (c, a + b)
We know that
Area of triangle ABC = Δ = 1/2 [x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)]
Let us substitute the values
Δ = 1/2 [a (c + a - a - b) + b (a + b - b - c) + c (b + c - c - a)]
By further simplification
Δ = 1/2 [a (c - b) + b (a - c) + c (b - a)]
Δ = 1/2 [ac - ab + ab - bc + bc - ac]
So we get
Δ = 1/2 [0]
Δ = 0
Therefore, the area of the triangle is 0.
Q19: If the distance between the points (4, p) and (1, 0) is 5, then the value of p is
(a) 4 only
(b) ± 4
(c) – 4 only
(d) 0
Correct Answer is Option (b)
We know that
The distance between two points P(x1, y1) and Q(x2, y2) is
The points given are (4, p) and (1, 0)
Let us apply the distance formula
By squaring on both sides
25 = (4 - 1)2 + p2
25 = 32 + p2
By further calculation
25 = 9 + p2
p2 = 25 - 9 = 16
So we get
p = ±4
Therefore, the value of p is ±4.
Q20: If the points A (1, 2), O (0, 0) and C (a, b) are collinear, then
(a) a = b
(b) a = 2b
(c) 2a = b
(d) a = –b
Correct Answer is Option (c)
As the given points are collinear, it does not form a triangle
It means that the area of triangle is zero
We know that
Area of triangle with vertices (x1, y1), (x2, y2) and (x3, y3) is
The points given are
(x1, y1) = (1, 2)
(x2, y2) = (0, 0)
(x3, y3) = (a, b)
By substituting these valuesSo we get
-b + 2a = 0
2a = b
Therefore, if the points are collinear, then 2a = b.
EXERCISE 7.2
Q1: State whether the following statements are true or false. Justify your answer.
ΔABC with vertices A(-2, 0), B(0, 2) and C(2, 0) is similar to ΔDEF with vertices D(-4, 0), F(4, 0) and E(0, 4).
Given, vertices of ∆ ABC are A(-2, 0) B(2, 0) and C(0, 2)
Vertices of ∆ DEF are D(-4, 0) E(4, 0) and F(0, 4)
We have to check if the triangles ABC and DEF are similar.
By the property of similarity,
The corresponding sides must be in proportion.
So, the side length of each triangle is calculated using the distance formula and verified whether it is proportional.
The distance between two points P (x₁ , y₁) and Q (x₂ , y₂) is
√[(x₂ - x₁)2 + (y2 - y₁)2]
The side length of ∆ ABC are
AB = √[(2 - (-2))2 + (0 - 0)2] = √(4)2 = √16 = 4
BC = √[(0 - 2)2 + (2 - 0)2] = √[(2)2 + (2)2] = √(4 + 4) = 2√2
AC = √[(0 - (-2))2 + (2 - 0)2] = √[4 + 4] = 2√2
The side length of ∆ DEF are
DE = √[(4 - (-4))2 + (0 - 0)2] = √(8)2 = 8
EF = √[(0 - 4)2 + (4 - 0)2] = √[(-4)2 + (4)2] = √(16 + 16) = √32 = 4√2
DF = √[(0 - (-4))2 + (4 - 0)2] = √(16 + 16) = √32 = 4√2
Now, AB/DE = BC/EF = AC/DF
4/8 = 2√2/4√2 = 2√2/4√2 = 1/2
So, the corresponding sides are in proportion.
Therefore, ∆ ABC ⩬ ∆ DEF
Q2: State whether the following statements are true or false. Justify your answer.
Point P (– 4, 2) lies on the line segment joining the points A (– 4, 6) and B (– 4, – 6).
Given, line segment joining the points A(-4, 6) and B(-4, -6)
We have to determine if the point P(-4, 2) lies on the line segment.
A line segment joining the point Q (x1 , y1) is
y - y1 = m(x - x1)
Where, m is the slope.
The slope of the line joining two points P (x1 , y1) and Q (x2 , y2) is is given by m = (y2 - y1)/(x2 - x1)Here, A(-4, 6) and B(-4, -6
Slope, m = -6 - 6/(-4 - (-4) = -12/0 = ∞
Now, the line segment is y - 6 = (12/0)(x - (-4))
(y - 6)(0) = -12(x + 4)
0 = -12(x + 4x + 4 = 0 -------------- (1)
If the point P(-4, 2) lies on the line segment then it has to satisfy the equation (1),Put x = -4 in (1)
-4 + 4 = 0
0 = 0
Therefore, the point P lies on the line AB.
Q3: State whether the following statements are true or false. Justify your answer.
The points (0, 5), (0, –9) and (3, 6) are collinear.
Given, the points are (0, 5) (0, -9) and (3, 6).
We have to check if the points are collinear.
The area of a triangle with vertices A (x1 , y1) , B (x2 , y2) and C (x3 , y3) is 1/2[x1(y2 - y3) + x2(y3- y1) + x3(y1 - y2)]
To check for the points to be collinear, the area of the triangle must be zero.
Here, (x1 , y1) = (0, 5), (x2 , y2) = (0, -9) and (x3 , y3) = (3, 6)
Area of triangle = 1/2[0(-9 - 6) + 0(6 - (-9)) + 3(5 - (-9))
= 1/2[0 + 0 + 3(5 + 9)]
= 1/2[3(14)]
= 3(7)
= 21
Area of the triangle ≠ 0
Therefore, the given points are not collinear.
Q4: State whether the following statements are true or false. Justify your answer.
Point P (0, 2) is the point of intersection of y–axis and perpendicular bisector of line
segment joining the points A (–1, 1) and B (3, 3).
Given, a line segment joining the points A(-1, 1) and B(3, 3)
We have to determine if the point P(0, 2) is the point of intersection of the y-axis and perpendicular bisector of the given line segment.
We know that any point lying on the perpendicular bisector of the line segment joining two points is equidistant from the two points.
The perpendicular bisector joining the two points are A(-1, 1) and B(3, 3)
To check if the point P lies on the perpendicular bisector, then distance between PA must be equal to distance between PB i.e., PA = PB
The distance between two points P (x1 , y1) and Q (x2 , y2) is√[(x2 - x1)2+(y2 - y1)2]
To find distance between P(0, 2) and A(-1, 1)
PA = √[(-1 - 0)2+(1 - 2)2] = √[(-1)2+(-1)2] = √(1+1) = √2
To find distance between P(0, 2) and B(3, 3)
PB = √[(3 - 0)2+(3 - 2)2] = √[(3)2+(1)2] = √(9+1) = √10
It is clear that PA ≠ PB
Therefore, point P(0, 2) does not lie on the perpendicular bisector of the line segment.
Q5: State whether the following statements are true or false. Justify your answer.
Points A (3, 1), B (12, –2) and C (0, 2) cannot be the vertices of a triangle.
Given, the points are A(3, 1) B(12 , -2) and C(0, 2)
We have to determine if the given points represent the vertices of a triangle.
We know that,
A triangle can be formed from any three line segments provided the sum of the lengths of any two of the segments is greater than the length of the third.
The distance between two points P (x₁ , y₁) and Q (x₂ , y₂) is
√[(x2 - x1)2+(y2 - y1)2]
The length of AB = √[(12 - 3)2+(-2 - 1)2]
= √[(9)²+(-3)²]
= √(81 + 9)
= √90
AB = 3√10
The length of BC = √[(0 -12)2+(2 - (-2))2]
= √[(-12)2+(4)2]
= √(144 + 16)
= √160
BC = 4√10
The length of AC = √[(0 - 3)2+(2 - 1)2]
= √[(-3)2+(1)2]
= √(9 + 1)
AC = √10
Now, sum of the two sides of a triangle = AB + AC
= 3√10 + √10
= 4√10
= BC
So, AB + AC ⪈ BC
Therefore, the given points do not form the vertices of a triangle.
Q6: State whether the following statements are true or false. Justify your answer.
Points A (4, 3), B (6, 4), C (5, –6) and D (–3, 5) are the vertices of a parallelogram.
Given, the points are A(4, 3) B(6, 4) C(5, -6) and D(-3, 5)
We have to determine if the given points are the vertices of a parallelogram.
By the property of parallelogram,
The opposite sides of a parallelogram are equal.
The distance between two points P (x₁ , y₁) and Q (x₂ , y₂) is
√[(x2 - x1)2+(y2 - y1)2]
AB = √[(6 - 4)2+(4 - 3)2]
= √[(2)2+(1)2]
= √(4 + 1)
AB = √5
BC = √[(5 - 6)2+(-6 - 4)2]
= √[(-1)2+(-10)2]
= √(1 + 100)
BC = √101
CD = √[(-3 - 5)2+(5 - (-6))2]
= √[(-8)2+(11)2]
= √(64 + 121)
CD = √185
AD = √[(-3 - 4)2+(5 - 3)2]
= √[(-7)2+(2)2]
= √(49 + 4)
AD = √53
It is clear that AB ≠ CD and BC ≠ AD
The opposite sides are not equal.
Therefore, the given points are not the vertices of a parallelogram.
Q7: State whether the following statements are true or false. Justify your answer.
A circle has its centre at the origin and a point P (5, 0) lies on it. The point
Q (6, 8) lies outside the circle.
Given, the centre of the circle is at the origin.
Point P(5, 0) lies on the circle.
We have to determine if the point Q(6, 8) lies outside the circle.
We know that, if the distance of any point from the centre is less than the radius, then the point is inside the circle equal to the radius, then the point is on the circle.
more than the radius, then the point is outside the circle.
To find the radius of the circle,
Radius of the circle is equal to the distance between the origin and the point P(5, 0)
The distance between two points P (x1 , y1) and Q (x2 , y2) is
√[(x2 - x1)2+(y2 - y1)2]
So, OP = radius of the circle = √[(5 - 0)2+(0 - 0)2]
= √[(5)2+0]
= √25
OP = 5
Distance between the origin and Q(6, 8) = √[(6 - 0)²+(8 - 0)²]
= √[(6)²+(8)²]
= √(36 + 64)
= √100
OQ = 10
We observe that OQ > OP
The distance of the point OQ is greater than the radius of the circle.
Therefore, the point Q lies outside the circle.
Q8: State whether the following statements are true or false. Justify your answer.
The point A (2, 7) lies on the perpendicular bisector of line segment joining the points P (6, 5) and Q (0, – 4).
Given, the line segment joining the points P(6, 5) and Q(0, -4)
We have to determine if the point A(2, 7) lies on the perpendicular bisector of the line segment.
We know that any point lying on the perpendicular bisector of the line segment joining two points is equidistant from the two points.
The perpendicular bisectors joining the two points are P(6, 5) and Q(0, -4)
To check if the point A lies on the perpendicular bisector, then distance between PA must be equal to distance between QA i.e., PA = QA
The distance between two points P (x1 , y1) and Q (x2 , y2) is
√[(x2 - x1)2 + (y2 - y1)2]
The distance between the points P(6, 5) and A(2, 7) = √[(2 - 6)2 + (7 - 5)2]
= √[(-4)2 + (2)2]
= √(16 + 4)
= √20
= 2√5
The distance between the points Q(0, -4) and A(2, 7) = √[(2 - 0)2 + (7 - (-4))2]
= √[(2)2 + (11)2]
= √(4 + 121)
= √125
= 5√5
PA ≠ QA
Therefore, point A(2, 7) does not lie on the perpendicular bisector of the line segment joining the given points.
Q9: State whether the following statements are true or false. Justify your answer.
Point P (5, –3) is one of the two points of trisection of the line segment joining the points A (7, – 2) and B (1, – 5).
Given, the line segment joining the points A(7, -2) and B(1, -5)
We have to check if the P(5, -3) is one of the two points of trisection of the line segment joining the given points.
By section formula,
The coordinates of the point P(x, y) which divides the line segment joining the points A (x₁ , y₁) and B (x2 , y2) internally in the ratio k : 1 are [(kx2 + x1)/k + 1 , (ky2 + y1)/k + 1]
P(5, -3) divides the line segment A(7, -2) and B(1, -5) internally in the ratio k:1
So, (5, -3) = [k(1) + (7))/k + 1 , (k(-5) + (-2))/k + 1]
(5, -3) = [k + 7/k + 1, -5k - 2/k + 1]
Now, k + 7/k + 1 = 5
k + 7 = 5(k + 1)
k + 7 = 5k + 5
By grouping,
5k - k = 7 - 5
4k = 2
k = 2/4
k = 1/2
The point P(5, -3) divides the line segment AB in the ratio 1:2.
Therefore, point P is the point of trisection of AB.
Q10: State whether the following statements are true or false. Justify your answer. Points A (–6, 10), B (–4, 6) and C (3, –8) are collinear such that AB =2/9 AC .
Given, the points are A(-6, 10) B(-4, 6) and C(3, -8)
We have to check if the points are collinear and prove that AB = 2/9 AC.
The area of a triangle with vertices A (x1 , y1) , B (x2 , y2) and C (x3 , y3) is
1/2[x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)]
To check for the points to be collinear, the area of the triangle must be zero.
Here, (x1 , y1) = (-6, 10), (x2 , y2) = (-4, 6) and (x3 , y3) = (3, -8)
Area of triangle = 1/2[-6(6 - (-8)) + -4(-8 - 10) + 3(10 - 6)
= 1/2[-6(14) + -4(-18) + 3(4)]
= 1/2[-84 + 72 + 12]
= 1/2[-84 + 84]
= 0
Area of the triangle = 0
Therefore, the points are collinear.
The distance between two points P (x1 , y1) and Q (x₂ , y₂) is
√[(x₂ - x₁)² + (y₂ - y1)²]
The distance between the points A(-6, 10) and B(-4, 6)
AB = √[(-4 - (-6))² + (6 - 10)²]
= √[(2)² + (-4)²]
= √(4 + 16)
= √20
= 2√5
The distance between the points A(-6, 10) and C(3, -8)
AC = √[(3 - (-6))² + (-8 - 10)²]
= √[(9)² + (-18)²]
= √(81 + 324)
= √405
= 9√5
Now, 2/9 AC = 2/9(9√5) = 2√5 = AB
Therefore, AB = 2/9 AC
Q11: State whether the following statements are true or false. Justify your answer. The point P (–2, 4) lies on a circle of radius 6 and centre C (3, 5).
Given, the circle with radius 6 and centre C(3, 5)
We have to determine if the point P(-2, 4) lies on the circle.
We know that, if the distance of any point from the centre is
- less than the radius, then the point is inside the circle
- equal to the radius, then the point is on the circle.
- more than the radius, then the point is outside the circle.
The distance between two points P (x1 , y1) and Q (x2 , y2) is
√[(x2 - x1)2 + (y2 - y1)2]
The distance between P(-2, 4) and C(3, 5)
PC = √[(3 - (-2))2 + (5 - 4)2]
= √[(5)2 + (1)2]
= √(25 + 1)
PC = √26
It is clear that PC < Radius of the circle
The distance between the point P from the centre is less than the radius of the circle.
Therefore, the point lies inside the circle.
Q12: State whether the following statements are true or false. Justify your answer. The points A (–1, –2), B (4, 3), C (2, 5) and D (–3, 0) in that order form a rectangle.
ABCD will form a rectangle if
(i) It is a parallelogram . (ii) diagonals are equal.
For parallelogram : Diagonals bisect each other.
i.e., Mid point of AC = Mid point of BD is
i.e. ( -1 + 22, -2 + 52 ) = ( 4 - 32, 3 + 02 )
⇒ ( 12, 32 ) = ( 12, 32 )
Conclusion: ABCD is a parallelogram.
Diagonal AC:
AC = √((2 + 1)² + (5 + 1)²) = √(9 + 49)
⇒ AC = √58 units
Diagonal BD:
BD = √((-3 - 4)² + (0 - 3)²)
⇒ BD = √(49 + 9) units
⇒ BD = √58 units
∴ Diagonals AC = Diagonal BD
Hence , ABCD is a rectangle.
|
127 videos|584 docs|79 tests
|
FAQs on NCERT Exemplar: Coordinate Geometry - 1 - Mathematics (Maths) Class 10
| 1. What is the importance of coordinate geometry in Class 10 mathematics? |  |
| 2. How do you find the distance between two points in coordinate geometry? |  |
| 3. What is the formula to find the midpoint of a line segment in coordinate geometry? |  |
| 4. How do you determine the slope of a line given two points? |  |
| 5. Can coordinate geometry be applied to real-life situations? |  |