NCERT Exemplar: Some Applications of Trigonometry | Mathematics (Maths) Class 10 PDF Download
Q.1. If a pole 6 m high casts a shadow 2√3 m long on the ground, find the Sun’s elevation.
Ans: 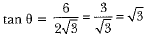
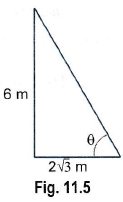 ⇒ θ = 60°
⇒ θ = 60°
Q.2. If the angle of elevation of a tower from a distance of 100 m from its foot is 60°, then what will be the height of the tower?
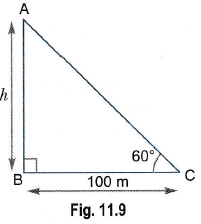 Ans: Let h be the height of the tower.
Ans: Let h be the height of the tower.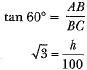
h = 100√3 m
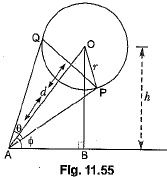
Q.3. A spherical balloon of radius r subtends an angle θ at the eye of an observer. If the angle of elevation of its centre is φ, find the height of the centre of the balloon.
Ans: In Fig. 11.55, O is the centre of the balloon, whose radius OP = r and ∠PAQ = θ. Also, ∠OAB = φ. Let the height of the centre of the balloon be h. Thus OB = h.
In ΔOAP, we have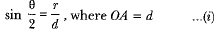
 Also in ΔOAB,
Also in ΔOAB,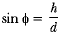 ...(ii)
...(ii)
From (i) and (ii), we get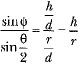 or
or

Q.4. If the angle of elevation of a cloud from a point h metres above a lake is α and the angle of depression of its reflection in the lake is β, prove that the height of the cloud is 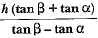
Ans: Let AB be the surface of the lake and let P be a point of observation (Fig. 11.58) such that AP = h metres. Let C be the position of the cloud and C' be its reflection in the lake. Then, CB = C'B. Let PM be perpendicular from P on CB. Then, ∠CPM = α and ∠MPC‘ = β. Let CM = x.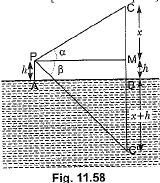 Then, CB = CM + MB = CM + PA = x + h
Then, CB = CM + MB = CM + PA = x + h
In ΔCPM, we have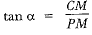
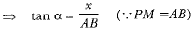
⇒ AB = x cot α
In ΔPMC’, we have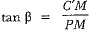
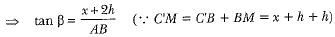
⇒ AB = (x + 2h) cotβ ...(ii)
From (i) and (ii), we have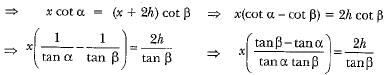
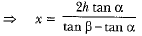
Hence, the height CB of the cloud is given by
CB = x + h ⇒ 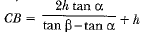
⇒ 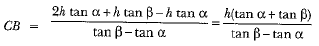
Q.5. The lower window of a house is at a height of 2 m above the ground and its upper window is 4 m vertically above the lower window. At a certain instant, the angles of elevation of a balloon from these windows are observed to be 60° and 30° respectively. Find the height of the balloon above the ground.
Ans: Let the height of balloon = h m
In rt. ΔGDC,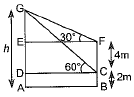
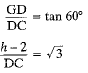
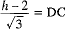 ...(i)
...(i)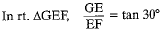
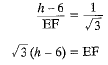
According to question
DC = EF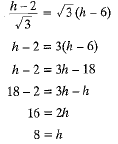
Height of the balloon above the ground is 8 m.
|
127 videos|584 docs|79 tests
|
FAQs on NCERT Exemplar: Some Applications of Trigonometry - Mathematics (Maths) Class 10
| 1. What are some real-life applications of trigonometry? |  |
| 2. How do we use trigonometry to calculate the distance between two objects? |  |
| 3. What is the importance of trigonometry in navigation and satellite communication systems? |  |
| 4. How is trigonometry used in analyzing waveforms in physics and engineering? |  |
| 5. In what ways is trigonometry used in designing structures like bridges and towers? |  |
















