Class 10 Maths Chapter 11 Previous Year Questions - Areas Related to Circles
Previous Year Questions 2017
Q10: A chord PQ of a circle of radius 10 cm subtends an angle of 60° at the centre of circle. Find the area of major and minor segments of the circle. (Delhi 2017)
View AnswerAns: Radius of the circle = 10 cm
Central angle subtended by chord AB = 60°
Area of minor sector OACB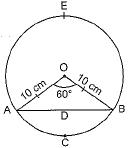
Area of equilateral triangle OAB formed by radii and chord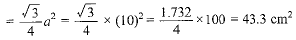
∴ Area of minor segment ACBD
= Area of sector OACB - Area of triangle OAB
= (52.38 - 43.30) cm2 = 9.08 cm2
Area of circle = πr2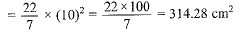 
∴ Area of major segment ADBE
= Area circle - Area of minor segment
= (314.28 - 9.08) cm2 = 305.20 cm2
Q11: In the given figure, ΔABC is a right-angled triangle in which ∠A is 90°. Semicircles are drawn on AB, AC and BC as diameters. Find the area of the shaded region. (Al 2017)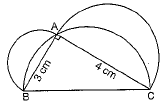
View AnswerAns: In right triangle ABC.
AB2 + AC2 = BC2
⇒ (3)2 + (4)2 = BC2 ⇒ 9 + 16 = BC2 ⇒ 25 = BC2
∴ BC = 5 cm
Now, Area of shaded region = Area of semicircle on side AB + area of semicircle on side AC - area of semicircle on side BC + area of ΔABC
Now, Area o f semicircle on side AB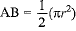 
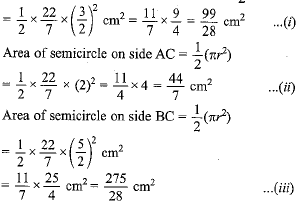
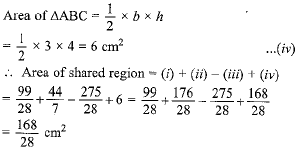
Hence area of the shaded region = 6 cm2
Q12: In Fig. 12.51, O is the centre of the circle with AC = 24 cm , AB = 7 cm and ∠BOD = 90°. Find the area of the shaded region. (CBSE (AI) 2017)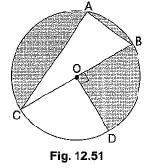
View AnswerAns: In right angle triangle ABC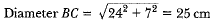
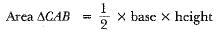
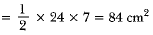
Area of shaded region = area of semicircle - area of ΔCAB + area of quadrant BOD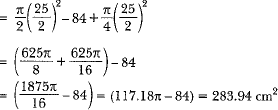
Previous Year Questions 2016
Q13: In Fig. 12.34, O is the centre of a circle such that diameter AB =13 cm and AC = 12 cm. ISC is joined. Find the area of the shaded region. (Take k = 3.14) (CBSE (AI) 2016)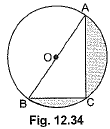
View AnswerAns: In ΔABC, ∠ACB = 90° (Angle in the semicircle)
∴ BC2 + AC2 = AB2
∴ BC2 = AB2 -AC2
= 169 - 144 = 25
∴ BC = 5 cm
Area of the shaded region = area of semicircle - area of right AABC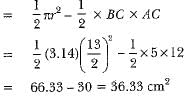
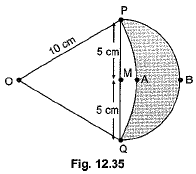
Q14: In Fig. 12.35, are shown two arcs PAQ and PBQ. Arc PAQ is a part of circle with centre 0 and radius OP while arc PBQ is a semi-circle drawn on PQ as diameter with centre M.
If OP = PQ = 10 cm show that area of shaded region is 25 
(CBSE (Delhi) 2016)
View AnswerAns: Since OP = PQ = QO
⇒ APOQ is an equilateral triangle
∴ ∠POQ = 60°
Area of segment PAQM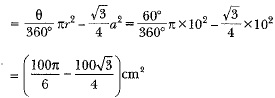
Area of semicircle with M as centre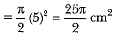 
Area of shaded region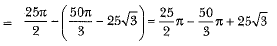 
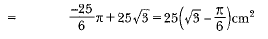
Q15: In figure, the boundary of shaded region consists of four semicircular arcs, two smallest being equal. If diameter of the largest is 14 cm and that of the smallest is 3.5 cm, calculate the area of the shaded region. 
(Foreign 2016)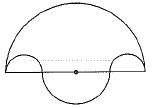
View AnswerAns: Given AD = 14 cm, AB = CD = 3.5 cm
∴ BC = 7 cm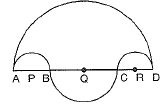
Area of shaded region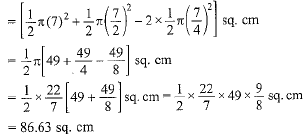
Q16: Find the area of the shaded region in Fig. 12.23, where a circular arc of radius 6 cm has been drawn with vertex 0 of an equilateral triangle ΔOAB of side 12 cm as centre. (NCERT, CBSE (F) 2016)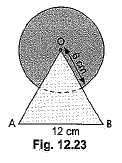
View AnswerAns: We have, radius of circular region = 6 cm and each side of ΔOAB = 12 cm.
∴ Area of the circular portion
= area of circle - area of the sector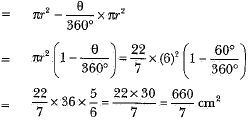
Now, area of the equilateral triangle OAB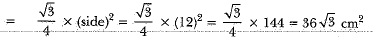
∴ Area of shaded region = area of circular portion + area of equilateral triangle OAB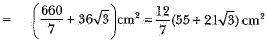
Q17: An elastic belt is placed around the rim of a pulley of radius 5 cm. (Fig. 12.46). From one point C on the belt, the elastic belt is pulled directly away from the centre O of the pulley until it is at P, 10 cm from the point O. Find the length o f the belt that is still in contact with the pulley. Also find the shaded area. (Use π = 3.14 and √3 = 1.73) (CBSE Delhi 2016)
View AnswerAns: 
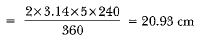
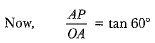
PA = 5√S cm = BP (Tangents from an external point are equal)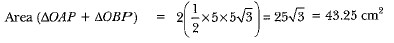
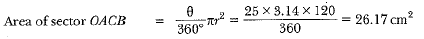
Shaded area = 43 .25 - 26 .17 = 17.08 cm2
Q18: In Fig. 12.47, a sector OAP of a circle with centre O, containing angle 0. AB is perpendicular to the radius OA and meets OP produced at B. Prove that the perimeter of shaded region is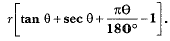 
(CBSE (AI) 2016)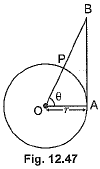
View AnswerAns: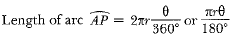 
In right ΔAOB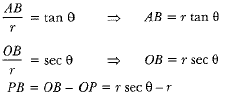
Perimeter of shaded region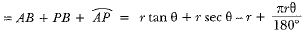 
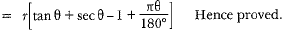
Q19: Find the area of the shaded region in Fig. 12.48, where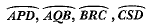 
are semicircles of diameter 14 cm, 3.5 cm, 7 cm and 3.5 cm respectively. 
(CBSE (E) 2016)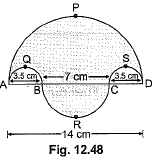
View AnswerAns: Area of shaded region = 
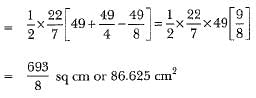
Previous Year Questions 2015
Q20: In figure, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and distance between AB and DC = 14 cm. If arcs of equal radii 7 cm with centres A, B, C and D have been drawn, then find the area of the shaded region. (Foreign 2015)
View AnswerAns: Area of shaded region = area of trapezium - (area of 4 sectors)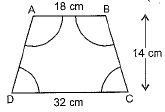
Total area of all sector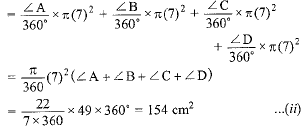
[Sum of angles of a quadrilateral is 360°]
From (i) and (ii),
Area of shaded region = 350 - 154 = 196 cm2
Q21: Find the area of the shaded region given in Fig. (Delhi 2015)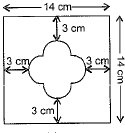
View AnswerAns: Side of the square = 14 cm
Area of the square = a2
= 142 - 196 cm2
Let radius of a semicircle=x
radius of two semicircles = 2x
side of inner square = diameter of semicircle = 2x
According to figure 2x + 2x = 8
4x = 8 ⇒ x = 2 cm
⇒ Side of inner square = 4 cm
Area of unshaded region = area of inner square + 4 (Area of a semicircle)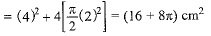
∴ Area of shaded region = area of square - area of unshaded region
= (196-16-871) cm2 = (180-8π) cm2
= 180-8 x 3.14 = 180-25.12 = 154.88 cm2
|
63 videos|271 docs|99 tests
|
FAQs on Class 10 Maths Chapter 11 Previous Year Questions - Areas Related to Circles
| 1. What is the formula to find the area of a sector of a circle? |  |
| 2. How can we find the length of an arc in a circle? | |
| 3. How do we calculate the area of a circle when only the circumference is given? | |
| 4. Can we find the area of a segment of a circle without knowing the angle? | |
| 5. How do we calculate the area of a circle inscribed in a triangle? | |
|
4.6K Views |
|
4.65/5 Rating |
|
Dec 23, 2024 Last updated |
|
Explore Courses for Grade 10 exam
|
|
MCQs
,shortcuts and tricks
,video lectures
,Exam
,Sample Paper
,Semester Notes
,practice quizzes
,mock tests for examination
,past year papers
,Class 10 Maths Chapter 11 Previous Year Questions - Areas Related to Circles
,Class 10 Maths Chapter 11 Previous Year Questions - Areas Related to Circles
,Class 10 Maths Chapter 11 Previous Year Questions - Areas Related to Circles
,Important questions
,study material
,Objective type Questions
,Summary
,ppt
,Previous Year Questions with Solutions
,Extra Questions
,Viva Questions
,Free
;
Previous Year Questions: Areas Related to Circles - 2 Free PDF Download
Importance of Previous Year Questions: Areas Related to Circles - 2
Previous Year Questions: Areas Related to Circles - 2 Notes
Previous Year Questions: Areas Related to Circles - 2 Grade 10
Study Previous Year Questions: Areas Related to Circles - 2 on the App
|
© EduRev
|
Education Revolution
|
|
