Class 10 Maths Chapter 9 Previous Year Questions - Some Application of Trigonometry
Previous Year Questions 2024
Q1: From a point on the ground, which is 30 m away from the foot of a vertical tower, the angle of elevation of the top of the tower is found to be 60º. The height (in metres) of the tower is: (CBSE 2024)(a) 10√3
(b) 30√3
(c) 60
(d) 30
View AnswerAns: (b)
Let BC be the tower and A be the observation point.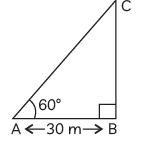
AB = 30 m
∠CAB = 60º
Let, BC = h m
In ΔCBA,
tan 60º = BC/AB
⇒ √3 = h/30
⇒ h = 30√3 m
Q2: A man on a cliff observes a boat at an angle of depression of 30º which is approaching the shore to the point immediately beneath the observer with a uniform speed. Six minutes later, the angle of depression of the boat is found to be 60º. Find the time taken by the boat form here to reach the shore. (CBSE 2024)
View AnswerAns:
Let AB be the cliff and observer is at point A. Initially the boat is at P after 6 min. it reaches to Q.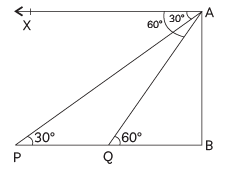
∠XAQ = ∠AQB = 60º
Let the speed of boat be x m/min.
So, distance, PQ = speed × time
= x × 6
= 6x meter
Let it takes t min to reach from Q to B. So distance
BQ = x × t
= tx meter.
In ΔAB P,
⇒
⇒
⇒
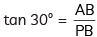
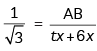
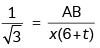
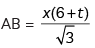...(i)In ΔABQ.
⇒
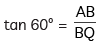
....(ii)From (i) and (ii)
⇒ x(6 + t) = 3xt
⇒ x(6 + t) = 3xt
⇒ t + 6 = 3t
⇒ 2t = 6
⇒ t = 3 min.
Previous Year Questions 2023
Q3: If a pole 6 m high casts a shadow 2√3 m long on the ground, then sun's elevation is (CBSE 2023)(a) 60º
(b) 45º
(c) 30º
(d) 90º
View AnswerAns: (a)
Let θ be the sun’s elevation.
Then tanθ = BC/AB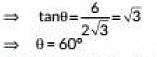
Q4: A straight highway leads to the foot of a tower. A man standing on the top of the 75 m high observes two cars at angles of depression of 30° and 60° which are approaching the foot of the tower. If one car is exactly behind the other on the same side of the tower, find the distance between the two cars. (Use √3 = 1.73) (CBSE 2023)
View AnswerAns: Let the tower be CD and points A and B be the positions of two cars on the highway.
Height of the tower CD = 75 m.
In ΔDCB,
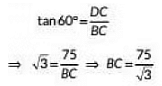
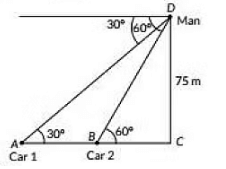
Now, In ΔACD,
Q5: From the top of a 7 in high building the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 30º. Determine the height of the tower. (2023)
View AnswerAns: Let AE be the building with height 7 m and BD be the tower with height h m.
In ΔABC,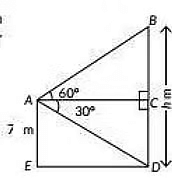
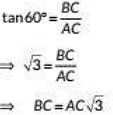---(i)
From (i) and (ii). we get
BC = 7√3 x √3 = 21m
∴ Height of the tower = 8C + CD
= 21 m + 7 m
= 28 m
Q6: A Ladder set against a wall at an angle 45º to the ground. If the foot of the ladder is pulled away from the wall through a distance of 4 m, its top slides a distance of 3 m down the wall making an angle 30° with the ground. Find the final height of the top of tire ladder from the ground and length of the ladder. (2023)
View AnswerAns: Let AE = CD = y be the length of the ladder and h be the final height of the top of the ladder from the ground.
In ΔABE, tan 45o = AB/BE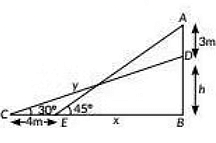
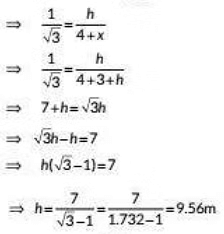
Previous Year Questions 2022
Q7: Two boats are sailing in the sea 80 m apart from each other towards a cliff AB. The angles of depression of the boats from the top of the cliff are 30º and 45° respectively, as shown in the figure. Find the height of the cliff. (2022)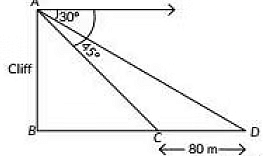
View AnswerAns: Let assume that AB be the cliff of height h m and Let the boats are at C and D.
Now, it is given that the angle of depression from B to C and D are 30° and 45° respectively.
It is also given that CD = 80 m
Let assume that BD = x m
Now, In right-angle triangle ABD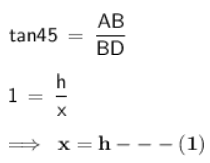
Now, In right-angle triangle ABC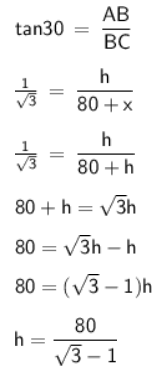
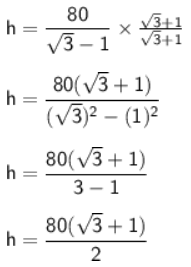
h = 40(√3 + 1)
h = 40(1.732 + 1)
h = 40 x 2.732
⇒ h = 109.28 m
Q8: The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, then find the height of the building. (2022)
View AnswerAns: Let AB be the tower of height 50m and CD be the building of height h m.
Now, in ΔABD,
Now, in ΔBDC,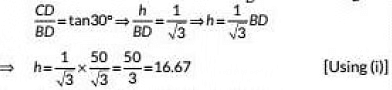
Thus the height of the building in 16.67m
Q9: In figure, AB is tower of height 50 m. A man standing on its top, observes two cars on the opposite sides of the tower with angles of depression 30° and 45° respectively. Find the distance between the two cars. (2022)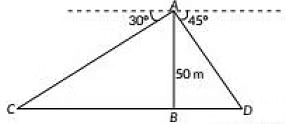
View AnswerAns: C and D be the position of two cars.
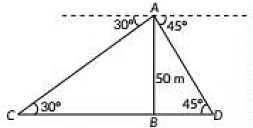
In ΔABD, we have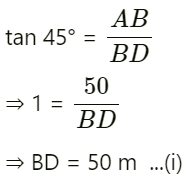
In ΔABC, we have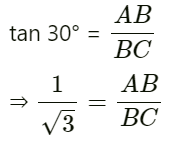
⇒ BC = AB√3 = 50√3 m ...(ii)
From equations (i) and (ii), we get
CD = BC + BD
= ( 50√3 + 50 ) m
= 50 (√3 + 1 ) m
= 50(1.732 + 1)
= 50 × 2.732
= 136.6 m
Thus, the distance between two cars is 136.6 m.
Q10: An aeroplane when flying at a height of 3125 in from the ground passes vertically below another plane at an instant when the angles of elevation of the two planes from the same point on the ground are 30° and 60° respectively. Find the distance between the two planes at that instant. (2022)
View AnswerAns: Let A and C be the position of two aeroplanes. Let distance between the two aeroplanes be x m.
In ΔCBD, we have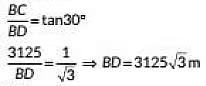
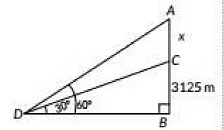
In ΔABD, we have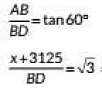
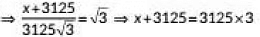
⇒ x + 3125 = 9375
⇒ x = 6250
∴ The distance between to planes at that instant in 6250m
Q11: The shadow of a tower standing on a level ground is found to be 40 m longer when the Sun's altitude is 30° than when it is 60°. Find the height of the tower. (2022)
View AnswerAns: Let AB be the tower of height b m and let shadow of tower when sun's altitude is 60° is x i.e. BC = x In ΔABC. we have
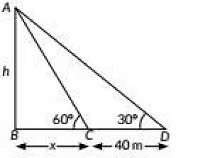
In ΔABD. we have
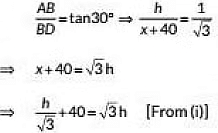
Q12: The tops of two poles of heights 20 m and 28 m are connected with a wire. The wire is Inclined to the horizontal at an angle of 30°. Find the length of the wire and the distance between the two poles (2022)
View AnswerAns: Let length of the wire be BD and the distance between the two poles be BE Le.. AC = x m
Here, height of the larger pole. CD = 28 m
Height of smaller pole, AB = 20 m
DE = CD - CE
⇒DE = 28 - 20
= 8 m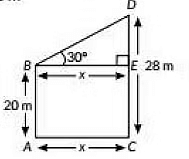 
In ΔBDE, we have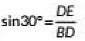 
= 8 x 1.73
= 13.84
∴ The distance between two planes , BE is 13.84 m.
Q13: Two men on either side of a cliff 75 m high observe the angles of elevation of the top of the cliff to be 30° and 60°. Find the distance between the two men. (2022)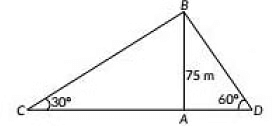
View AnswerAns: Given, AB = 75 m be the cliff and C, D be the positions of two men.
Now, in ΔABD,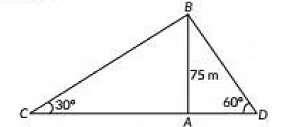
Q14: From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45°. If the bridge is at a height of 8 m from the banks, then find the width of the river. (2022)
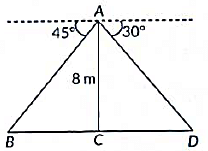
View AnswerAns: We have, B and D represents points on the bank on opposite sides of the river. Therefore, BD is the width of the river.
Let A be a point on the bridge at a height of 8 m.
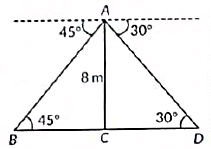
In ΔABC,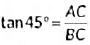 
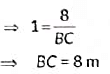
In ΔACD, 
Q15: The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. From a point Y, 40 m vertically above X, the angle of elevation of the top Q of tower is 45°. Find the height of the tower PQ and the distance PX. (Use √3 = 1.73) (2022)
View AnswerAns: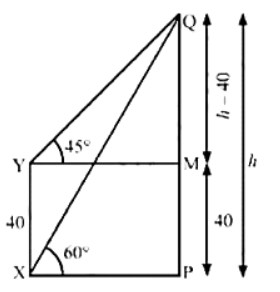 
We have
XY = 40m,∠PXQ = 60° and ∠MYQ = 45°
Let PQ = h
Also, MP = XY = 40m, MQ = PQ - MP = h - 40
In ΔMYQ,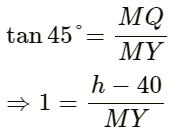
⇒ MY = H - 40
⇒ PX = MY = h - 40 ................(1)
Now , in ΔMXQ,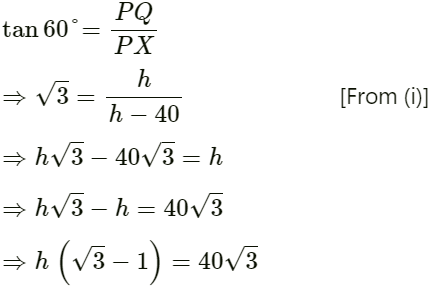
⇒ h = 20√3 (√3 + 1 )
⇒ h = 60 + 20√3
⇒ h = 60 + 20 × 1.73
⇒ h = 60 + 34.6
∴ h = 94.6m
So, the height of the tower PQ is 94. 6 m.
Q16: The straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30°. which is approaching the foot of the tower with a uniform speed. Ten seconds later the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point. (2022)
View AnswerAns: Let h be the height of the tower and D be the initial position of car and let DB = a, AB = b
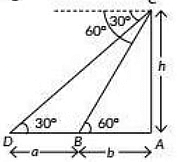
Now, in ΔCAD,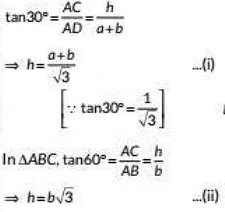
Eliminating h, from (i) and (ii). we have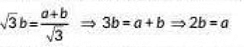
As the car covers distance a i.e.. 2b in 10 seconds.
So. it will take 5 seconds to reach the foot of the tower as covering b distance.
Q17: Case Study: Kite Festival (2022)
Kite festival is celebrated in many countries at different times of the year. In India, every year 14th January is celebrated as International Kite Day. On this day many people visit India and participate in the festival by flying various kinds of kites.
The picture given below shows three kites flying together
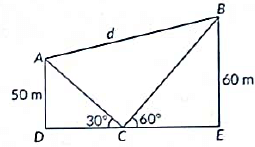
In Fig. the angles of elevation of two kites (Points A and B) from the hands of a man (Point C) are found to be 30° and 60° respectively. Taking AD = 50 m and BE = 60 m, find
(i) the lengths of strings used (take them straight) for kites A and B as shown in figure.
(ii) the distance ‘d' between these two kites
View AnswerAns: (i) : Given , AD = 50 m. BE = 60 m
Let the lengths of strings used for kite A be AC and for kite B be BC
Now , in ΔADC ,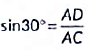 
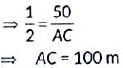
In ΔBEC,
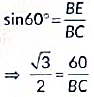
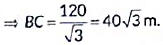
Hence, AC = 100 m and BC = 40√3 m
(ii) Since, the distance between these two kites is d.
ΔABC is a right angle triangle (∵∠ACB = 90°)
Now, in ΔABC, by using Pythagoras theorem, we have
BA2 = BC2 + AC2
Hence, the distance between these two kites is 121.65 m.
Previous Year Questions 2021
Q18: A man on the top of a vertical tower observes a car moving at a uniform speed coming directly towards it. If it takes 18 minutes for the angle of depression to change from 30o to 60o. How soon after this will the car reach the tower? (2021) View AnswerAns: Let AB be the tower of height h m and D be the initiaI position of the car and C be the position of car after 18 minutes.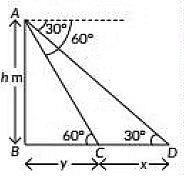
Let CD = x and BC = y
In ΔABD, we have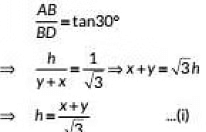
In ΔABC, we have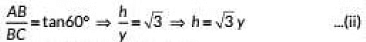
On comparing (i) and (ii), we have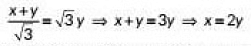
Distance x is covered by car in 18 minutes. Distance 2y is covered by car in 18 minutes.
Hence, Distance y is covered by car in 9 minutes.
Previous Year Questions 2020
Q19: In figure, the angle of elevation of the top of a tower from a point C on the ground, which is 30m away from the foot of the tower, is 30o Find the height of the tower. (2020)
View AnswerAns: Here, AB is the tower.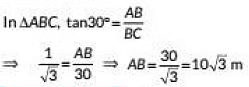
Q20: The ratio of the length of a vertical rod and the length of its shadow is 1: √3. Find the angle of elevation of the Sun at that moment. (2020)
View AnswerAns: Let AC be the length of vertical rod, AB be the length of its shadow and 0 be the angle of elevation of the sun.
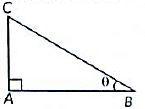
In ΔABC,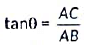 
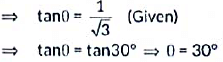
Q21: The rod AC of a TV disc antenna is fixed at right angles to the wall AB and a rod CD is supporting the disc as shown in the figure. If AC = 1.5 m long and CD = 3 m, then find
(i) tanθ
(ii) secθ + cosecθ (2020)
View AnswerAns: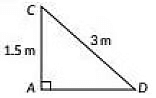
In ΔACD, ∠CAD = 90°AD2 = CD2 - AC2 [By Pythagoras theorem]
= (3)2 - (1.5)2= 9 - 2.25 = 6.75 m2
Q22: From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower
(Use √3 = 1.73) (2020)
View AnswerAns: Let P be the point of observation. AB is the building of height 20 m and AC is the transmission tower.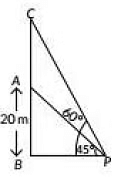
⇒ 20+AC = 20√3
⇒ AC = 20√3 - 20 = 20(√3 -1)
⇒ AC=20(1.73 - 1)= 20 x 0.73
⇒AC= 14.6 m
Thus, the height of the tower is 14.6 m.
Q23: A statue 1.6 m tall, stands on the top of a pedestal. From a point on the ground the angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
(Use √3 = 1.73) (CBSE 2020)
View AnswerAns: In the figure, A represents the point of observation, DC represents the statue and BC represents the pedestal.
Now, in right ΔABC, we have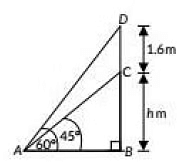
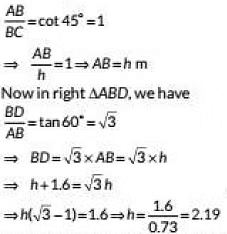
Thus , the height of the pedestal is 2.19 m.
Previous Year Questions 2019
Q24: The angles of depression of the top and bottom of a 8 m tall building from the top of a tower are 30° and 45° respectively. Find the height of the tower and the distance between the tower and the building. (2019) View AnswerAns: Let AB be the tower at height h m and CD he the building of height 6m and let x m be the distance between the lower and building.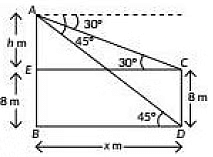
In ΔABD, we have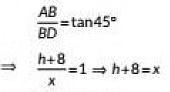
In ΔAEC, we have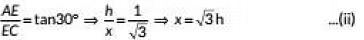
Put x = √3 in (i), we get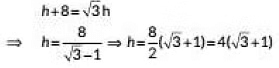
From (ii), we have
Now, The height or the Tower AB
and distance between tower and building = x = 4(3 + √3) m
Q25: As observed from the top of a lighthouse, 75 m high from the sea level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships. (2019)
View AnswerAns: Let AB be the lighthouse and C and D be the position of two ships.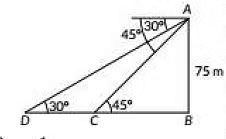
Now, In ΔABC
Now in ΔABD, we have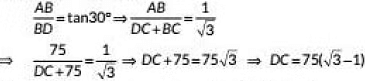
Hence, distance between two ships is 75(√3 - 1)
Q26: A man in a boat rowing away from a light house 100 in high takes 2 minutes to change the angle of elevation of the top of the fight house from 60° to 30°. Find the speed of the boat in metres per minute. [Use √3 = 1.732) (2019)
View AnswerAns: Let AB = 100 m be the height of the light house.
Let the initial distance be x m and angle is 60°.
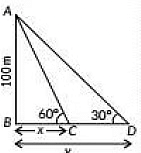
In ΔABC,
Now. after two minutes, new distance be y m and angle is 30°.
In ΔABD,
Speed of boat = Distance / Time
= 115.47 / 2
= 57.74 metres/minute
Q27: Amit, standing on a horizontal plane, finds a bird flying at a distance of 200 m from him at an elevation of 30°. Deepak standing on the roof of a 50 m high building. finds the angle of elevation of the same bird to be 45°. Amit and Deepak are on opposite sides of the bird. Find the distance of the bird from Deepak. (2019)
View AnswerAns: Here, A be the position of Amit, B be the position of bird and D be the position of Deepak standing on roof of the building CD of height 50 m.
In ΔAMB, we have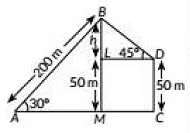
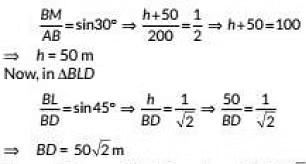
Hence, distance of bird from Deepak is 50√2 m.
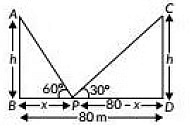
Q28: Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30° respectively. Find the height of the poles and the distances of the point from the poles. (2019)
View AnswerAns: Let AB and CD be two poles of height hm.
Let P be a point on road such that BP = x so that
PD= BD - BP = (80 - x)m
In ΔABP, h / x = tan60°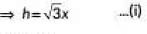
In ΔCDP,
Distance of point P from AB = 20 m Distance of point P from
CD = 80- 20 = 60 m
Height of each pole, h = 20 x 1.732 = 34.64 m
Q29: A boy standing on a horizontal plane finds a bird flying at a distance of 100 m from him at an elevation of 30°. A girl standing on the roof of a 20 m high building, finds the elevation of the same bird to be 45°. The boy and the girl are on the opposite sides of the bird. Find the distance of the bird from the girl. (Given √2= 1.414) (CBSE 2019)
View AnswerAns: Let P be the position of Bird B and G he the position of the boy and the girl respectively.
GN be the building at which the girl is standing.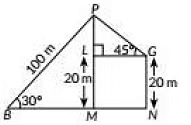
In ΔPMB,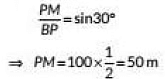
Now. PL = PM - LM = 50 - 20 = 30mIn ΔPLG,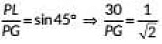
⇒ PG = 30√2 = 30 x 1.414 = 42.42 m
Hence , the bird is flying at a distance of 42 .42 m from the girl.
Q30: The angle of elevation of an aeroplane from point A on the ground is 60°. After a flight of 30 seconds, the angle of elevation changes to 30°. If the plane is flying at a constant height of 3600√3 metres, find the speed of the aeroplane. (2019)
View AnswerAns: Let P and Q be the two positions of the aeroplane.
Given, angle of elevation of the aeroplane in two positions P and Q from A is 60° and 30° respectively.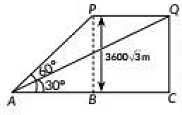
In ΔABP, we have
⇒ AC = 3600 x 3 = 10800 m
∴ Distance covered by aeroplane.
= PQ = BC = AC - AB = 10800 - 3600 = 7200 m
Thus, aeroplane travels 7200m in 30seconds.
Hence, speed of aeroplane = 7200/30
= 240m/ sec.
Q31: A moving boat is observed from the top of a 150 m high cliff, moving away from the cliff. The angle of depression of the boat changes from 60º to 45º in 2 minutes. Find the speed of the boat in m/hr. (CBSE 2019, 17)
View AnswerAns: Here, AB is the cliff of height 150 m, C and D are the two positions of a boat.
AB = 150 m, ∠ACB = 60° and ∠ADB = 45°
Let, the distance BC be ‘x’ m and CD be ‘y’ m.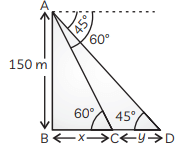
Now, in ∆ABC,
Using (i), we get
But, the time taken to cover distance ‘y’ or CD is 2 minutes i.e. 2 / 60 hr or, 1 / 30 hr
Then Speed = Distance / Time
Hence, the speed of the boat is 1500 √3 (√3 −1) m/hr
Previous Year Questions 2017
Q32: Raju, a painter, has to use a ladder to paint the high walls and ceilings of homes. When Raghu was observing Raju paint his house, he told his friend that he could calculate the height of the wall up to the point where the ladder reached by using his knowledge of trigonometry.
Raju used a ladder 15 m long that makes an angle of 60° with the wall. Find the height of the point where the ladder touches the wall. (CBSE 2017)
View AnswerAns: Let AC be the ladder of length 15 m, which is at the height AB i.e., ‘h’ m from the ground.
The ladder makes an angle of 60° with the wall.
∴ ∠CAB = 60°
Now, in ∆ABC,
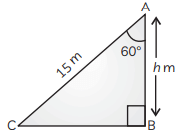cos 60° = AB / AC
⇒ 1 / 2 = h / 15
⇒ h = 7.5 m
Hence, the height of the point where the ladder touches the wall is 7.5 m.
|
126 videos|457 docs|75 tests
|
FAQs on Class 10 Maths Chapter 9 Previous Year Questions - Some Application of Trigonometry
| 1. What are the basic trigonometric ratios used in Class 10 applications of trigonometry? |  |
| 2. How do you apply trigonometry to solve real-life problems in Class 10? | |
| 3. What is the significance of the angle of elevation and depression in trigonometry? | |
| 4. Can you explain the concept of solving triangles in the context of trigonometry for Class 10? | |
| 5. What types of questions can be expected in exams regarding applications of trigonometry in Class 10? | |
|
15.3K Views |
|
4.92/5 Rating |
|
Dec 23, 2024 Last updated |
|
Explore Courses for Class 10 exam
|
|
Exam
,Summary
,ppt
,mock tests for examination
,Free
,Previous Year Questions with Solutions
,Extra Questions
,MCQs
,Class 10 Maths Chapter 9 Previous Year Questions - Some Application of Trigonometry
,shortcuts and tricks
,Important questions
,video lectures
,study material
,Viva Questions
,Sample Paper
,Semester Notes
,Class 10 Maths Chapter 9 Previous Year Questions - Some Application of Trigonometry
,practice quizzes
,Objective type Questions
,past year papers
,Class 10 Maths Chapter 9 Previous Year Questions - Some Application of Trigonometry
;
Previous Year Questions: Some Applications Of Trigonometry Free PDF Download
Importance of Previous Year Questions: Some Applications Of Trigonometry
Previous Year Questions: Some Applications Of Trigonometry Notes
Previous Year Questions: Some Applications Of Trigonometry Class 10
Study Previous Year Questions: Some Applications Of Trigonometry on the App
|
© EduRev
|
Education Revolution
|
|
