Class 10 Maths Previous Year Questions - Constructions (Old Syllabus)
| Table of contents |

|
| Previous Year Questions 2019 |

|
| Previous Year Questions 2018 |

|
| Previous Year Questions 2017 |

|
| Previous Year Questions 2016 |

|
Previous Year Questions 2019
Q1: Draw two concentric circles of radii 2 cm and 5 cm. Take a point P on the outer circle and construct a pair of tangents PA and PB to the smaller circle. Measure PA. [CBSE, Allahabad 2019] View Answer
View Answer 
Ans: Steps of Construction: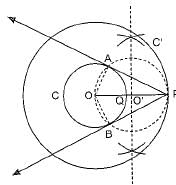
- Draw concentric circles of radius OQ = 2 cm and OP = 5 cm having same centre O.
- Mark these circles as C and C'.
- Points O, Q and P lie on the same line.
- Draw perpendicular bisector of OP, which intersects OP at O'.
- Take O' as centre, draw a circle of radius OO' which intersects circle C at points A and B.
- Join PA and PB, these are the required tangents.
- Length of these tangents are approx. 4.6 cm.
Justification:
Join OA and OB
OA ⊥ PA [Radius ⊥ to tangent]
In right angled ΔOAP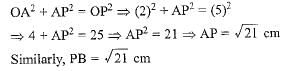
A pair of equal tangents can be drawn to a circle from an external common point outside the circle.
∴ PA = PB
Q2: Construct a ΔABC in which CA = 6 cm, AB = 5 cm and ΔBAC = 45°. Then construct a triangle whose sides are 3/5 of the corresponding sides of ΔABC. [Delhi 2019]
 View Answer
View Answer 
Ans: Steps of construction: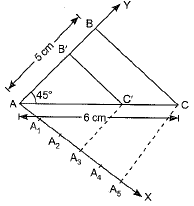
- A line segment AC = 6 cm is drawn.
- ∠CAB = 45° is constructed at A.
- An arc of 5 cm radius to be drawn with A as centre, cutting AY at B.
- B and C are joined. Then, ΔABC is constructed.
- An acute angle CAX is drawn below AC.
- Points A1, A2, A3, A4 and A5 are taken on AX, such that AA1 = A3A2 = A2A3 = A3A4 = A4A5
- A5 and C are joined.
- A3C' is drawn parallel to A5C, meeting AC at C' .
- C'B' is drawn parallel to CB, meeting AB at B'.
- AB'C' is the required triangle similar to ΔABC whose sides a 3/5 of the corresponding sides of ΔABC.
Q3: Two poles of equal heights are standing opposite to each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30°, respectively. Find the height of the poles and the distances of the point from the poles. [NCERT; CBSE 2019 (30/1/2)]
 View Answer
View Answer 
Ans: Let AB and CD be two poles of equal height & metre and let P be any point between the poles, such that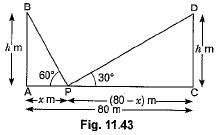 ∠APB = 60° and ∠DPC = 30°
∠APB = 60° and ∠DPC = 30°
The distance between two poles is 80m. (Given)
Let AP = x m, then PC = (80 - x) m
Now, in ΔAPB, we have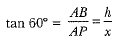
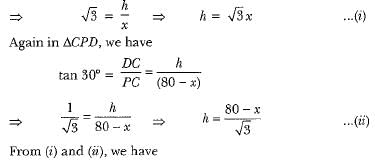
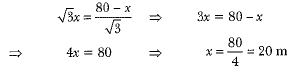
Now, putting the value of x in equation (i), we have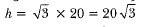
Hence, the height of the pole is 20 √3 m and the distance of the point from first pole is 20 m and that of the second pole is 60 m.
Q4: A boy standing on a horizontal plane finds a bird flying at a distance of 100 m from him at an elevation of 30°. A girl standing on the roof of 20 metre high building, finds the angle of elevation of the same bird to be 45°. Both the boy and the girl are on opposite sides of the bird. Find the distance o f bird from the girl. [Given √2 = 1.414] [CBSE 2019 (30/5/1)]
 View Answer
View Answer 
Ans: Let B be the position of bird. O and P be the positions of boy and girl respectively and PQ be the building
We have, ∠AOB = 30° and, ∠BPM = 45°
In ΔAOB, we have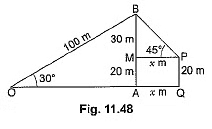
Hence, distance of bird from girl is 30 √2 m.
Previous Year Questions 2018
Q5: Construct a triangle with sides 6 cm, 8 cm and 10 cm. Construct another triangle whose sides are 3/5 of the corresponding sides of the original triangle. [CBSE 2018 (C)] View Answer
View Answer 
Ans: Steps of construction:
- Draw ΔABC, such that
AB = 8 cm, BC = 6 cm
AC = 10 cm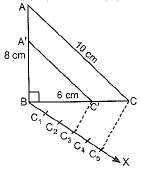
- Draw any ray BX making an acute angle with BC on the side opposite to the vertex A.
- Draw 5 equal marks, C1, C2, C3, C4, C5 such that BC1 = C1C2 = C2C3 = C3C4 = C4C5
- Join CC5. Draw C3C' || C5C, where C' is any point on BC
- Draw C'A' || AC
- ΔA'BC' is the required triangle.
Previous Year Questions 2017
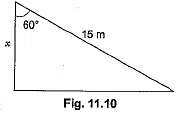
Q6: A ladder 15 m long makes an angle of 60° with the wall. Find the height of the point where the ladder touches the wall. [CBSE(F) 2017] View Answer
View Answer 
Ans:
Q7: The ratio of the height of a tower and the length of its shadow on the ground is 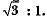 What is the angle of elevation of the sun? [CBSE Delhi 2017]
What is the angle of elevation of the sun? [CBSE Delhi 2017]
 View Answer
View Answer 
Ans:

Q8: Draw a line segment of length 8 cm and divide it internally in the ratio 4 : 5. [Delhi 2017]
 View Answer
View Answer 
Ans: Steps of construction:
- Draw a line segement AB of length 8 cm.
- Draw any ray AX making an acute angle with AB.
- Locate 9(i.e. 4+5) points A1, A2, A3, ... A9 on AX so that AA1 = A1A2 = ... A8A9
- Join A9B.
- Through the point A4 draw a line parallel to A9B by making an angle equal to ∠AA9 B at A4 intersecting AB at point P.
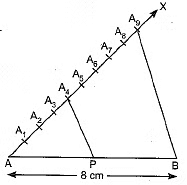
Then AP : PR = 4 : 5
Q9: If a tower 30 m high, casts a shadow 10 √3 m long on the ground, then what is the angle of elevation of the sun? [CBSE (Al) 2017]
 View Answer
View Answer 
Ans: In ΔABC
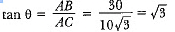
⇒ tan θ = tan 60°⇒ θ = 60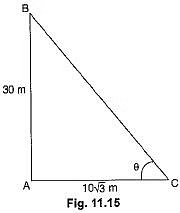
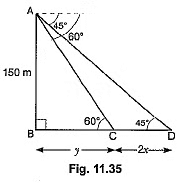
Q10: A moving boat is observed from the top of a 150 m high cliff moving away from the cliff. The angle of depression of the boat changes from 60° to 45° in 2 minutes. Find the speed of the boat in m/h. [CBSE Delhi 2017]
 View Answer
View Answer 
Ans: Let the speed of boat be x m/min
∴ CD = 2x
In ΔABC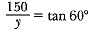
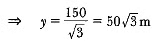
In ΔABD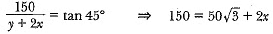
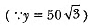
 ⇒
⇒ 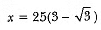
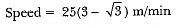
∴ 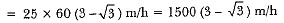
Q11: From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower. [NCERT, CBSE Delhi 2017]
OR
From the top of a 7 m high building, the angle of elevation of the top of a tower is 60° and the angle of depression of its foot is 45°. Find the height of the tower. [Use √3 = 1.732] [CBSE (F) 2017]
 View Answer
View Answer 
Ans: Let PQ be the building of height 7 metres and AB be the cable tower. Now it is given that the angle of elevation of the top A of the tower observed from the top P of building is 60° and the angle of depression of the base B of the tower observed from P is 45°. (Fig. 11.38)
So, ∠APR = 60° and ∠QBP = 45°
Let QB = x m, AR = h m then, PR = x m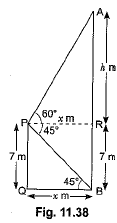 Now, in ΔAPR, we have
Now, in ΔAPR, we have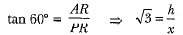
 ...(i)
...(i)
Again, in ΔPBQ we have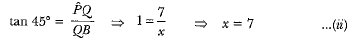
Putting the value of x in equation (i), we have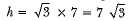
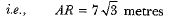
So, the height of tower
Q12: A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point. [NCERT, CBSE Delhi 2017 (C)]
 View Answer
View Answer 
Ans: Let OA be the tower of height h, and P be the initial position of the car when the angle of depression is 30°.
After 6 seconds, the car reaches to Q such that the angle of depression at Q is 60°. Let the speed of the car be v metre per second. Then,
PQ = 6v (∴ Distance = speed x time)
and let the car take i seconds to reach the tower OA from Q (Fig. 11.41). Then, OQ = vt metres.
Now, in ΔAQO, we have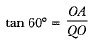
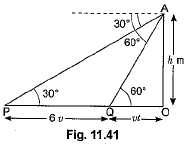
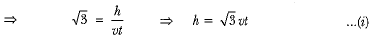
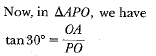
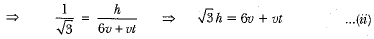
Now, substituting the value of h from (i) into (ii), we have
Hence, the car will reach the tower from Q in 3 seconds.
Q13: From the top of a tower, 100 m high, a man observes two cars on the opposite sides of the tower and in same straight line with its base, with angles of depression 30° and 45°. Find the distance between the cars. [Take √3= 1.732] [CBSE (AI) 2017]
 View Answer
View Answer 
Ans: Let AO be the tower of height 100 m. Car B and Car C are in opposite direction and at distance of x m and y m respectively.
In ΔABO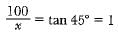
⇒ x = 100 ...(i)
In ΔACO, 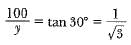
⇒ 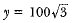 ...(ii)
...(ii)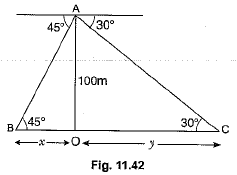 Distance between the cars - x + y
Distance between the cars - x + y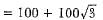 [From equation (i) and (ii)]
[From equation (i) and (ii)]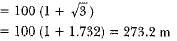
Q14: The shadow of a tower at a time is three times as long as its shadow when the angle of elevation of the sun is 60°. Find the angle of elevation of the sun at the time of the longer shadow. [CBSE(F) 2017]
 View Answer
View Answer 
Ans: Let AB be the flagstaff and BC be the length of its shadow when the Sun rays meet the ground at an angle of 60°. Let 0 be the angle between the Sun rays and the ground when the length of the shadow of the flagstaff is BD. Let h be the height of the flagstaff (Fig. 11.52).
Let BC = x ∴ BD = 3x and CD = 2x
In ΔABC, we have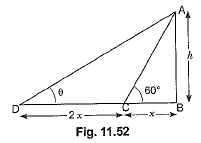
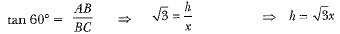
In ΔADB, we have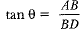
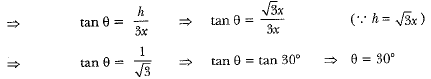
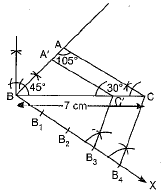
Q15: Construct a triangle ABC with side BC = 7 cm, ∠B = 45°, ∠A = 105°. Then construct another triangle whose sides are 3/4 times the corresponding sides of the ΔABC. [AI 2017]
 View Answer
View Answer 
Ans: In ΔABC,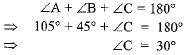
 Steps of Construction:
Steps of Construction:
- Draw a line segment BC = 7 cm. At point B, draw ∠B = 45° and at C, draw ∠C = 30° and get ΔABC.
- Draw an acute CBX on the base BC at point B (In the downward direction). Mark the ray BX with four equal points B1, B2, B3 and B4 such that BB1 = B1B2 = B2B3 = B3B4.
- Join B4 to C. Draw B3C'||B4C.
- At C', draw C'A'||AC.
- ΔABC' is the required triangle.
Q16: Draw an isosceles triangle ABC in which the base BC is 8 cm long and its altitude AD through A is 4 cm long. Then draw another triangle whose sides are 2/3 of the corresponding sides of the ΔABC. [AI 2017 (C)]
 View Answer
View Answer 
Ans: Steps of construction: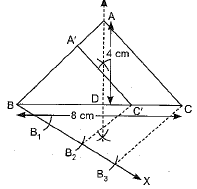
Draw an isosceles ΔABC in which BC = 8 cm, AD = 4 cm and AB = AC
Draw an acute angle CBX below BC at point B.
Draw three equal marks B1, B2, B3 on BX, such that
BB1 = B1B2 = B2B3
Join B3C, draw B2C' || B3C.
At point C', draw C'A' || AC.
ΔA'BC' is the required isosceles triangle.
Q17: From the top of a hill, the angles of depression of two consecutive kilometre stones due east are found to be 45° and 30° respectively. Find the height of the hill. [CBSE (E) 2017]
 View Answer
View Answer 
Ans: Let the height of the hill be h m, C and D are two consecutive stones having a distance of 1000 m between them and 4C = x m.
In ΔABC,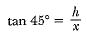
⇒ x = h ...(i)
In ΔABD,
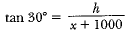
⇒ 
⇒ 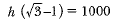
⇒ 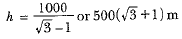
Hence, the height of the hill 
Previous Year Questions 2016
Q18: In Fig. 11.13, AB is a 6 m high pole and CD is a ladder inclined at an angle of 60° to the horizontal and reaches up to a point D of pole. If AD = 2.54 m, find the length of the ladder. (Use √3 =1.73) [CBSE Delhi 2016]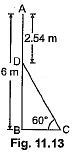
 View Answer
View Answer 
Ans: DB = (6 - 2.54)m = 3.46 m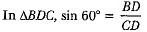
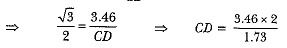
∴ DC = 4m
Q19: An observer, 1.7 m tall, is 20 √3 m away from a tower. The angle of elevation from the eye of the observer to the top of the tower is 30°. Find the height of the tower. [CBSE (F) 2016]
 View Answer
View Answer 
Ans: Let AB be the height of tower and DE be the height of observer.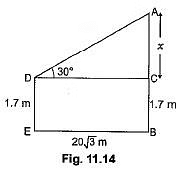
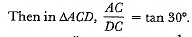
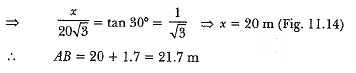
Q20: A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 5 m. From a point on the ground the angles of elevation of the top and bottom of the flagstaff are 60° and 30° respectively. Find the height of the tower and the distance of the point from the tower. (Take √3 = 1.732) [CBSE (F) 2016]
 View Answer
View Answer 
Ans: Let height of tower be x m and distance of point from tower be y m.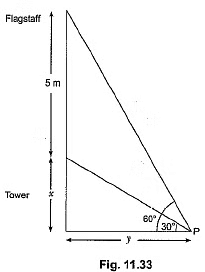
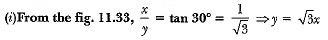
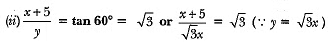
⇒ x + 5 = 3x ⇒ x = 5/2 = 2.5
Height of tower = 2.5 m
Distance of point from tower = y = √3x
= (2.5 X 1.732) or 4.33 m
Q21: Two men on either side of a 75 m high building and in line with base of building observe the angle of elevation of the top of the building as 30° and 60°. Find the distance between the two men. (Use √3 = 1.73) [CBSE (F) 2016]
 View Answer
View Answer 
Ans:
ln ΔABM1 ,
Let AB be the building having height 75 m and the angles of elevation are 30° and 60° from the point M1 and M2 respectively;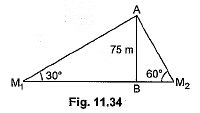
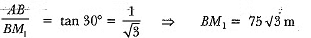
In ΔABM2,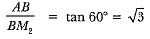
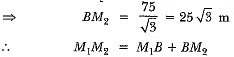
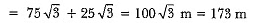
∴ Distance between two men = 173 m.
|
81 videos|339 docs|98 tests
|
FAQs on Class 10 Maths Previous Year Questions - Constructions (Old Syllabus)
| 1. What are the basic tools required for constructions? |  |
| 2. How can we construct a perpendicular bisector of a line segment? |  |
| 3. What is the significance of constructions in mathematics? |  |
| 4. How can we construct an angle bisector of a given angle? |  |
| 5. What are some common errors to avoid while making constructions? |  |




















